Метод снятия индикаторных диаграмм

Отчет по лабораторной работе №2

На тему

« Исследование плоскорадиального установившегося фильтрационного потока несжимаемой жидкости в однородном пласте»

По дисциплине: ____ Подземная гидромеханика_ ___

(наименование учебной дисциплины согласно учебному плану)

 

Выполнил: студент гр. НГ-09-2 _ / Чеботов А. Ю./

^{(подпись) (Ф.И.О.)}

 

Проверил: преподаватель / Гладков П.Д./

^{(должность) (подпись) (Ф.И.О.)}

 

Санкт-Петербург

Цель: исследование плоскорадиального установившегося фильтрационного потока несжимаемой жидкости в однородном пласте.

Теоретические сведения:

Характерными особенностями такого потока являются:

1) Частицы жидкости движутся параллельно в одной и той же плоскости, проходящей через ось скважины;

2) Прямолинейные траектории движения частиц жидкости в любой плоскости, перпендикулярной оси скважины, радиально сходятся в одной точке на оси скважины;

3) Картины движения вдоль всех и любой траектории движения одинаковы, а следовательно для изучения такого потока достаточно изучить, движение вдоль одной любой траектории, т.е. поток является одномерным по радиусу.

Такой установившийся фильтрационный поток называется одномерным плоскорадиальным и фильтрация в нем несжимаемой жидкости по закон Дарси описывается:

(1)

где Р – P_(r) - давление на расстоянии r от оси скважины, Па;

r - расстояние от оси скважины до рассматриваемой точки, м.

Распределение давления в круговом пласте:

,где (2)

P_(r) - установившееся давление на расстоянии г от скважины. Па:

Р_к - установившееся контурное (пластовое) давление на контуре питания r_k, Па;

Р_г - установившееся давление в скважине, Па;

г_с - радиус скважины, м;

R- радиус контура питания пласта, м;

r - текущий радиус, м.

Из формулы (2) видно, что распределение давления представляет собой логарифмическую зависимость давления от радиуса и графически представляется логарифмической кривой.

Градиент давления:

gradP = dP / dr= 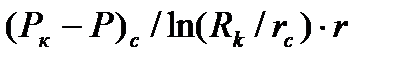. (3)

 

 

Скорость фильтрации:

. (4)

Дебит (объемный расход) скважины (по формуле Дюпюи)

,где (5)

Q - дебит скважины, м³/с;

k - проницаемость пласта, м;

h - толщина пласта, м:

μ - динамическая вязкость, Па с.

Время движения частицы жидкости от контура питания радиуса R_k забоя скважины радиуса r_c:

t= , где (6)

 

r₀ - начальное положение частицы жидкости;

r - текущее положение частицы жидкости.

Средневзвешенное по объему перового пространства пластовое давление

(7)

Дебит скважины можно выразить в виде уравнения притока

Q = K ΔP, где (8)

K- коэффициент продуктивности скважины, м³/(с Па).

В промысловых условиях часто используется размерность коэффициента продуктивности [К] – м³/(сут МПа).

Δ Р= Р_к - Р_с - депрессия на пласт, Па.

Коэффициент продуктивности скважины:

, (9)

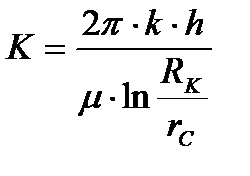. (10)

Коэффициент гидропроводности пласта в призабойной зоне скважины:

. (11)

 

Коэффициент проницаемости пласта:

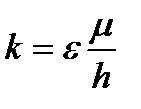. (12)

Задачи:

1) Изучить распределение давления, градиента давления и скорости фильтрации в залежи круговой формы при установившейся фильтрации несжимаемой жидкости по закону Дарси;

2) Определить дебит скважины, средневзвешенное по объему порового пространства пластовое давление и время движения частицы от контура питания до забоя скважины;

3) Изучить элементы гидродинамических исследований скважин на установившихся режимах фильтрации – построение индикаторных диаграмм и, на базе их обработки, определить и оценить фильтрационные свойства пласта (коэффициенты продуктивности, гидропроводности и проницаемости), при следующих исходных данных:

Таблица 1

Исходные данные

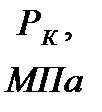
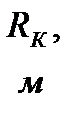
				, кг/м3
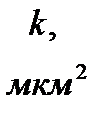
9,7	7,2		0,18		2,0		0,4

 

где – давление на контуре питания;

– давление на забое скважины;

– радиус контура питания;

– радиус скважины;

– плотность жидкости;

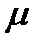– динамическая вязкость жидкости;

– толщина пласта;

– проницаемость;

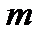– пористость.

 

 

Таблица 2

Показатели работы скважины на различных режимах

РС1, МПа	Q1, т/сут	РС2, МПа	Q2, т/сут	РС3, МПа	Q3, т/сут	РС4, МПа	Q4, т/сут	РС5, МПа	Q5, т/сут
7,2		7,7		8,2		8,7	86,8	9,2	43,4

Рис. 1. Схема плоскорадиального потока

Решение:

Определение закона распределения давления в пласте:

 

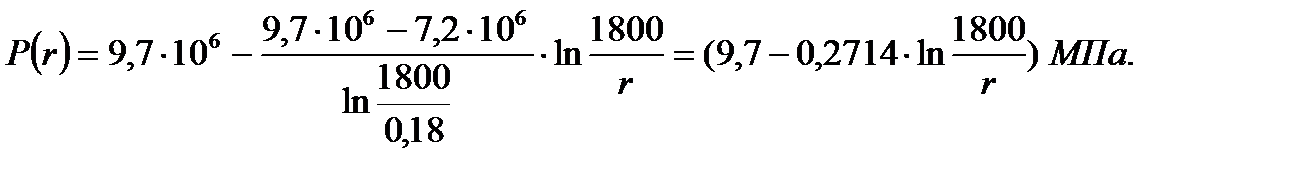
Таблица 3

Данные для построения зависимости Р(r)

r, м	P,МПа
0,18	7,2
	7,666
	8,103
	8,291
	8,727
	8,819
	8,916
	9,214
	9,352
	9,444
	9,512
	9,566
	9,632
	9,651
	9,668
	9,684
	9,7

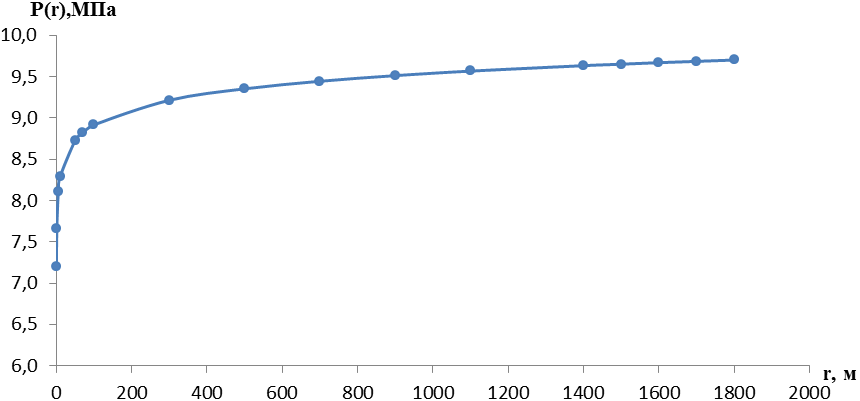
Рис. 2. График распределения давления в пласте

Определение градиента давления:

 

 

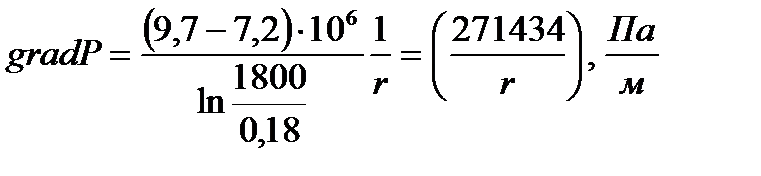
Таблица 4

Данные для построения зависимости gradР(r)

r,м	gradP(r),Па/м
0,18	1507966,667
	54286,8
	27143,4
	5428,68
	3877,629
	2714,34
	904,78
	542,868
	387,763
	301,593
	246,758
	193,881
	180,956
	169,646
	159,667
	150,797

Рис. 3. График распределения градиента давления в пласте .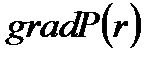

Определение скорости фильтрации:

 

 

Таблица 5

Данные для построения зависимости V(r)

r,м	V(r)·10-6,м/c
0,18	301,667
	54,3
	10,86
	5,43
	1,086
	0,775
	0,543
	0,181
	0,1086
	0,077
	0,060
	0,049
	0,039
	0,036
	0,034
	0,032
	0,03

 

Рис. 4. График распределения скорости фильтрации

 

Определение дебита скважины (по формуле Дюпюи):

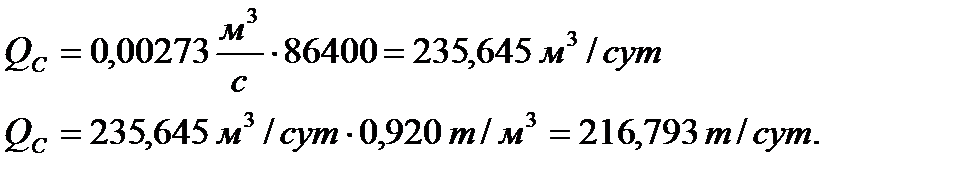
Средневзвешенное по объему порового пространства пластовое давление:

Время движения частицы от контура питания радиуса до забоя скважины радиуса :

Метод снятия индикаторных диаграмм

Рк

 

Рис. 5. Зависимость дебита Q от забойного давления P_C.

 

Давление на контуре питания: Р_К = 9,7МПа.

 

Рис. 6. Зависимость дебита Q от депрессии на пласт ΔP.

 

 

Коэффициент продуктивности скважины:

 

 

 

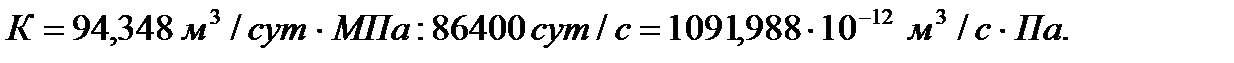
Уравнение притока жидкости к скважине:

 

,

где - коэффициент продуктивности скважины;

- депрессия на пласт, Па.

Тогда имеем уравнение следующего вида:

.

 

Коэффициент гидропроводности пласта в призабойной зоне скважины:

 

 

 

 

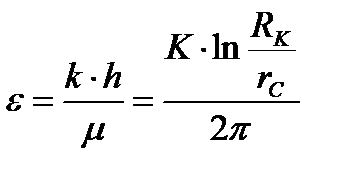
Коэффициент проницаемости пласта:

 

 

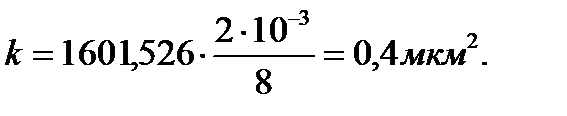
Выводы:

В ходе данной лабораторной работы были получены и построены следующие зависимости: распределения давления, градиента давления и скорости фильтрации в залежи круговой формы при установившейся фильтрации несжимаемой жидкости; был определен дебит скважины, равный:

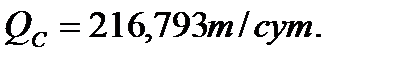Средневзвешенное по объему порового пространства пластовое давление: 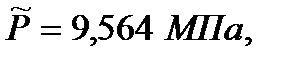и времени движения частицы от контура питания до забоя скважины: , а также были построены индикаторные диаграммы и, на базе их обработки, определены коэффициенты:

продуктивности: ,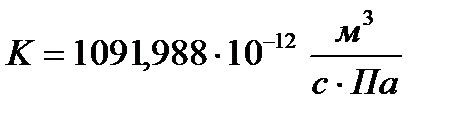

гидропроводности:

и коэффициент проницаемости: