ПредисловИЕ
Из многих широко используемых промышленных сталей особый практический и научный интерес представляют горячекатаные ферритно-перлитные стали. К ним относятся низкоуглеродистые и низколегированные стали; последние после горячей прокатки на современных станах имеют предел текучести 300…450 МПа. Объем производства этих сталей в последние годы быстро возрастает. В конструкциях повышенной прочности низкоуглеродистые нелегированные стали заменяются низколегированными.
Если в деталях и конструкциях все эти стали применяются в основном без специальной термической обработки, то их ферритно-перлитная структура ответственна за эксплуатационные свойства.
Основная цель настоящей работы – анализ прочности ферритно-перлитных сталей в зависимости от их макро-, мезо- и микроструктуры.
1. ГЛАВНАЯ ДИАГРАММА ЗАВИСИМОСТИ
ПРОЧНОСТЬ–ТРЕЩИНОСТОЙКОСТЬ–СТРУКТУРА
Цель работы – установление количественной зависимости между структурой и механическими свойствами стали.
Исследование включает следующие этапы.
1. Металлографический анализ ферритно-перлитных сталей с определением количественных характеристик структур.
2. Вычисление с помощью ЭВМ коэффициентов множественной регрессии эмпирического уравнения предела текучести с использованием результатов эксперимента.
3. Выбор оптимальных технологических обработок в промышленных условиях, обеспечивающих повышение конструктивной прочности стали.
В практике расчета конструкций обычно используют лишь значения предела текучести и реже – предела прочности. Учитывая изменения свойств материала в процессе эксплуатации и возможные перегрузки, расчетные рабочие напряжения большинства конструкций принимают равными некоторой части (коэффициент надежности) от предела текучести или предела прочности.
Хрупкое, неожиданное разрушение конструкций до наступления общей текучести показало, что механические свойства, определенные на стандартных гладких образцах, не всегда характеризуют поведение высокопрочного материала в рабочих условиях, так как не учитывают возникновение трещин в процессе изготовления или эксплуатации. Надежность работы детали в этом случае характеризуется сопротивлением материала распространению трещин, т. е. трещиностойкостью, или вязкостью разрушения. Эта характеристика позволяет рассчитать критические допустимые размеры трещины при определенной нагрузке.
При использовании упрочненных материалов расчет конструкций должен учитывать не только предел текучести, но и разрушающее напряжения, которое можно определить, зная характеристики вязкости разрушения. Накопленный к настоящему времени обширный экспериментальный материал дает возможность прийти к важному принципу любого упрочнения: повышение предела текучести не должно сопровождаться катастрофическим понижением трещиностойкости.
В общем случае задача повышения прочности сплава достигается образованием различных препятствий – барьеров, затрудняющих движение дислокаций. Если дислокации скапливаются около прочных барьеров, то у вершины этого плоского скопления возникают растягивающие напряжения. Эти напряжения с точки зрения большинства дислокационных теорий служат одной из главных причин зарождения трещин и хрупкого разрушения материалов. Чем прочнее заблокированы дислокации, тем сильнее подавлены процессы микро- и макропластической деформации сплава. Улучшить характеристики вязкости разрушения можно противоположным путем: развитием микро- и макропластической деформации.
Таким образом, для оптимального сочетания прочности и вязкости разрушения структура упроченного сплава наряду с торможением движущихся дислокаций или их блокировкой (повышение сопротивлению деформации) должна обладать способностью предотвращать опасность возникновения пиковых напряжений путем передачи деформации в соседние объемы (повышение вязкости разрушения). Следовательно, дислокации в решетке металла должны быть и заторможены (высокий предел текучести), в то же время должна сохраняться подвижность (высокая вязкость разрушения).
Основываясь на анализе физических явлений происходящих на микро-
и мезоструктурных уровнях при деформировании материалов и диаграмм конструктивной прочности (зависимость трещиностойкости от предела текучести), можно графически отобразить тройную зависимость предел текучести–трещиностойкость – структура материала.
Такая зависимость может иметь физический смысл, так как и предел текучести, и трещиностойкость – это структурно-чувствительные характеристики материала. Таким образом, два структурно-чувствительных показателя механического поведения материала связаны общим фактором – структурой, изменяющейся под воздействием различных упрочняющих обработок (рис. 1). На диаграмме показан возможный разброс данных sт и К Ic, увеличивающийся с ростом прочности материала.
Склонность промышленных сплавов к хрупкости или пластичности целесообразно оценивать, рассматривая величину противоречия между sт и вязкостью разрушения К Ic, dс, J Ic в обязательной связи со структурным состоянием сплава. Показатели, входящие в этот график, – напряжение течения, или начало активного и множественного движения дислокаций, sт и склонность к развитию хрупкой трещины от готового концентратора К Ic – определяются экспериментально и, следовательно, учитывают реальное структурное состояние сплава. Условная точка х делит диаграмму на две области: I – высокой надежности и II – повышенной хрупкости. Если реальный сплав (сталь) в соответствии со своим структурным состоянием (проведенным упрочнением, например, термической обработкой) располагается в области I, его служба безопасна, так как всякие случайные перегрузки (рост внешнего напряжения по ординате вверх) будут сниматься активной пластической деформацией в связи с низкими значениями sт и высокими значениями К Ic.
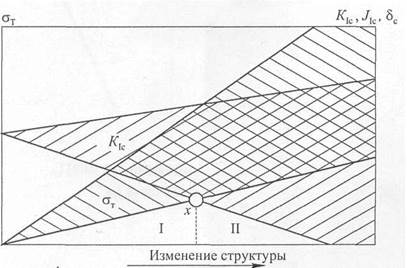
Рис. 1. Главная диаграмма конструктивной прочности материалов – принципиальная тройная зависимость предел текучести – трещиностойкость – структура материала. I – область надежной службы; II – область возможных разрушений; x – точка условного, относительного равновесия между sт и К Ic
Если этот же сплав сильно упрочнен (созданы активные препятствия движущимся дислокациям), то значительно возрастает sт и снижается К Ic. В этих условиях всякий пик внешней нагрузки сначала достигает критического значения К Ic, затем создаются благоприятные условия для развития хрупкого разрушения.
Для оценки возможности реального, эффективного упрочнения металлических сплавов, т. е. повышения предела текучести без снижения вязкости разрушения (верхние границы кривых на рис. 1), необходимо рассмотреть дислокационные механизмы повышения предела текучести и сопоставить их с возможным изменением вязкости разрушения.
Важным шагом в развитии структурной теории прочности стало установление нами связей структурных механизмов упрочнения не только с пределом текучести, но и вязкостью разрушения (трещиностойкостью)
sт, К Ic = f (sп, sд, sр, sф, sз) (1)
В этом модифицированном уравнении конструктивной прочности (так как в общую зависимость входит не только sт, но и К Ic), учтены и оба главных показателя конструктивной прочности, и возможные модели упрочнения на уровне теории дислокаций и дисклинаций.
На основании уравнения (1) эмпирически было получено упрощенное уравнение зависимости предела текучести sт от различных структурных факторов в виде многочлена, причем принято допущение, что члены многочлена не зависят друг от друга
sт = sп + sд + sр + sф + sз. (2)
Если раньше это уравнение использовали в основном при изучении теории упрочнения, то в последнее время наблюдается тенденция практического применения зависимости предела текучести от параметров структуры. На основе анализа членов этого уравнения в последние годы созданы новые материалы и виды обработки, приводящие к повышению конструктивной прочности. На рис. 2 показана схема изменения предела текучести и критического разрушающего напряжения при упрочнении сплавов по различным механизмам. Из рисунка видно, что при выборе упрочняющей обработки основную роль в повышении предела текучести следует отдавать членам sд.п.я, sф, sз.
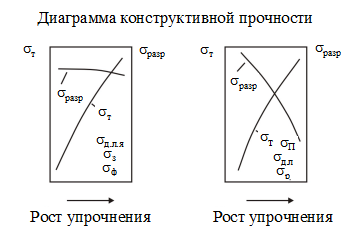
Рис. 2. Схема зависимости критического разрушающего напряжения (sразр) и напряжения течения (sт) от степени упрочнения по различным дислокационным механизмам – моделям:
sп – упрочнение от трения в решётке (сила Пайерлса–Набарро); sд.л. – упрочнение дислокациями «леса»; sд.п.я. – упрочнение дислокационными полигонными ячейками; sр – упрочнение растворенными атомами; sф – упрочнение дисперсными фазами; sз – упрочне- ние микроструктурными барьерами (зернами)
2. АНАЛИЗ ЧЛЕНОВ УРАВНЕНИЯ ПРЕДЕЛА ТЕКУЧЕСТИ
Рассмотрим более подробно члены уравнения предела текучести.
sп – напряжение трения решетки железа, или сила Пайерлса–Наббарро.
Это напряжение, необходимое для движения дислокации в зерне бесконечно большого размера при отсутствии каких-либо препятствий. sп существенно зависит от природы кристаллической решетки и температуры и колеблется от 18 до 69 МПа.
sд – упрочнение за счет взаимодействия дислокаций
sд = sд.л. + sд.п.я, (3)
где sд.л – это результат сопротивления дислокации за другими дислокациями, расположенными на ее пути, – дислокациями леса. Известна зависимость увеличения напряжения течения от плотности дислокаций леса
sд.л = a Gb r 1/2, (4)
где a – коэффициент, учитывающий особенности взаимодействия дислокаций; G – модуль сдвига, для стали – 8 × 104 МПа; b – вектор Бюргерса, равный 2,5 × 10–7 мм; r – плотность дислокаций (1/мм2).
sд.п.я – упрочнение границами полигонов, ячеек, субзерен.
В нашем случае последний вид упрочнения отсутствует, поэтому: sд = sд.л.
sр – упрочнение растворенными атомами.
Влияние легирующих элементов на повышение предела текучести обусловлено прежде всего искажениями кристаллической решетки, возникающими при образовании твердых растворов показана прямая зависимость (в определенных пределах концентрации) напряжения течения от концентрации легирующих элементов. Для оценки упрочнения обычно пользуются формулой
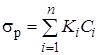 , (5)
, (5)
где Ki – коэффициент повышения напряжения на один весовой процент легирующего элемента, Сi – весовой процент легирующих элементов в твердом растворе.
Наибольший вклад в увеличение предела текучести вносит углерод, образующий твердый раствор внедрения. Коэффициент повышения предела текучести на один весовой процент углерода составляет 5700 МПа. Однако равновесная растворимость углерода в феррите при комнатной температуре очень мала, и поэтому упрочнение за счет растворенных атомов углерода в расчет не принимается.
Считается, что марганец, кремний и хром целиком входят в состав феррита и упрочняют последний. Именно эти элементы вносят основной вклад в упрочнение ферритно-перлитных сталей.
sф – упрочнение дисперсными фазами.
Поскольку, в исследуемых сталях при рассматриваемых термических обработках (отжиг и нормализация) выделений избыточных фаз не наблюдается, можно считать, что реальное упрочнение за счет дисперсных фаз в данном случае отсутствует.
sз – упрочнение микроструктурными барьерами.
В общем случае под sз понимают упрочнение, обусловленное наличием в структуре границ зерен, фаз или других высокоугловых границ. В ферритно-перлитных сталях имеются микроструктурные барьеры двух видов.
Во-первых, это граница ферритных зерен; их вклад в упрочнение (sз) вычисляется по формуле Петча–Холла
sз = К у d –1|2 , (6)
где К у – коэффициент, определяющий прочность блокирования дислокаций, d – диаметр зерна, мм.
Величина зерна зависит от состава стали, ее обработки давлением и термической обработки.
Во-вторых, перлитная составляющая в микроструктуре предполагает, что барьерами для движущихся дислокаций являются цементные пластины в перлите. Тогда пробеги дислокации ограничиваются межпластиночным расстоянием в перлите.
Примем допущение, что величина Δ в рассматриваемых сталях одинакова. Тогда вклад в упрочнение этими барьерами (sперл) выразим через количество перлита
sперл = К перл n, (7)
где К перл – эмпирический коэффициент, n – объемный процент перлита.
Применяя уравнение (7) к описанию предела текучести ферритно-перлитных сталей и принимая допущения, согласно которому sф и sд.п.я можно не учитывать, получим уравнение
sт = sп + sд + sр + sз,
где sд = sд.л = a Gb r 1/2 из (3) и (4);
sр = К Mn (%Mn) + KSi(%Si) + КCr(%Cr) из (5);
sз = К у d –1/2 + К перл n из (6) и (7).
Следовательно, рабочее уравнение будет иметь вид
sт = sп + a Gb r1/2 + К Mn(%Mn) + K si(%Si) + К Cr(%Cr) + К у d –1/2 + К перл n, (8)
где sт – физический предел текучести стали, МПа; sп - константа, сила Пайерлса–Наббарро, МПа; r - плотность дислокаций, 1/мм2; К Mn (%Mn), K si(%Si), КCr(%Cr) - коэффициенты, учитывающие процентное содержание по массе марганца, кремния и хрома, %; К перл – коэффициент, учитывающий объемную долю перлита, %; d – диаметр зерна феррита, мм; G – модуль сдвига стали, равный –
8 × 104 МПа; b - вектор Бюргерса, равный 2,5 × 10–7 мм; s n - принимается для всех исследуемых сталей одинаковым, его значение 280 МПа; К у – константа зернограничного упрочнения; a – коэффициент, учитывающий особенности взаимодействия дислокаций.
В полученном уравнении независимые переменные (r), (d), (n) могут быть определены экспериментально – металлографическим методом, а химический состав стали – по ГОСТ.
Коэффициенты при этих переменных a, К Mn, K si, К Cr, К у, К перл указывают вклад соответствующего фактора – переменной – в общую величину предела текучести.
Анализ численных значений найденных коэффициентов определенной группы сталей позволяет сознательно управлять их упрочнением.
Таким образом, задача данной работы включает: а) экспериментальное определение sт и независимых переменных, членов уравнения; б) вычисление коэффициентов при этих переменных методом регрессионного анализа с использованием ЭВМ.
3. МЕТОДЫ ЭКСПЕРИМЕНТАЛЬНОГО ОПРЕДЕЛЕНИЯ sт
И НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
3.1. Определение предела текучести стали (sт)
Испытание на растяжение (ГОСТ 1497) широко применяют для конструкционных сталей и сплавов.
Графическое изображение зависимости между напряжениями (или нагрузками) и деформациями материала (или перемещениями при деформировании) представляет собой диаграмму деформирования.
Испытательные машины имеют специальные приспособления, которые автоматически записывают диаграмму растяжения. На диаграмме по оси ординат откладываются действующие осевые нагрузки Р 1, а по оси абсцисс – деформации.
На рис. 3 показана типичная диаграмма растяжения отожженных или нормализованных малоуглеродистых сталей. Для этой диаграммы характерны следующие участки: 0–1 – упругая, обратимая деформация; максимальная нагрузка, соответствующая упругой деформации Р упр.; 1–2 – начало перемещения дислокаций, приводящее к необратимым смещениям в металле, т. е. к пластической деформации; 2–3 – стадия легкого скольжения, массового перемещения дислокаций, приводящего к необратимой пластической деформации без увеличения нагрузки. Это площадка текучести, ей соответствует нагрузка Р т; 3–4 – пластическая деформация сопровождающаяся ростом нагрузки до максимального значения Р макс. Это участок деформационного упрочнения; 4–5 – уменьшение нагрузки при возрастании деформации за счет образования в образце местного утонения – шейки – до разрушения образца в т. 5.
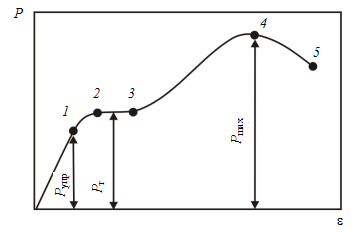
Рис. 3. Характерные участки и точки диаграммы
растяжения
Так как при обработке полученных данных площадь поперечного сечения образца, несмотря на утонение при деформации, принимают неизменной (F 0), то получают условные напряжения:
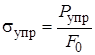 , (9)
, (9)
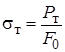 , (10)
, (10)
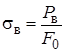 , (11)
, (11)
Эти величины принято выражать в мегапаскалях (МПа).
Пример определения sт по диаграмме растяжения (см. рис. 3). На диаграмме линейкой с точностью до 1 мм замеряют длину отрезка Р т в миллиметрах. С учетом масштаба вычисляют Р т в Н, определяют площадь поперечного сечения образца F 0 = bh в м2, где b – толщина образца, м; h – ширина образца, м. По формуле (10) находят физический предел текучести (1 МПа» 106 Н/м2).
3.2. Определение плотности дислокаций
Эта методика состоит в исследовании с помощью просвечивающего электронного микроскопа тончайшего металлического образца – фольги.
Существует несколько методов определения плотности дислокаций. Простейший из них заключается в измерении числа N – точек выхода дислокаций на поверхность фольги в кадре площадью F
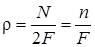 (12)
(12)
(число дислокаций в кадре n = N /2, так как подсчет на снимке ведется сразу по обеим поверхностям фольги).
Так как вследствие кристаллического строения металлов и особенностей электронно-микроскопических исследований часть дислокаций не попадает в поле зрения, то плотность дислокаций определяют по формуле
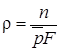 , (13)
, (13)
где 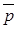 – вероятность того, что в данных условиях дислокация видна; для решетки ОЦК Р = 51/72.
– вероятность того, что в данных условиях дислокация видна; для решетки ОЦК Р = 51/72.
Пример. При изучении дислокационной структуры феррита в кадре (рис. 4), снятом при помощи электронного микроскопа, находится 14 дислокаций. Площадь кадра – 10–6 мм2.

Рис. 4. Дислокационная структура феррита, полученная при электронно-микроскопи- ческих исследованиях
Плотность дислокаций определится отношением:
r = 14/(51/72 × 10–6) = 2 × 107 1/мм2.
3.3. Определение процентного содержания элементов
Химический состав стали, т. е. содержание марганца, кремния, хрома, определяется в процессе выплавки стали и выражается в марке стали в виде цифр и условных букв. Данные химического анализа исследуемых марок сталей приведены в таблице.
Химический состав сталей
| № п/п | Марка стали | ГОСТ | Содержание элементов, % | |||||||||||
| Углерод | Кремний | Марганец | Хром | |||||||||||
| 08пс 15кп 09ГС 09Г2С 17ГС 14ХГС 20ХГСА 16Х 40ХС СтЗпс | - " - - " - - " - - " - - " - - " - - " - - " - | 0,08 0,20 0,15 0,41 0,12 0,12 0,17 0,14 0,20 0,15 0,41 0,18 | 0,11 0,27 0,05 0,27 0,27 0,65 0,5 0,5 1,10 0,27 1,40 0,10 | 0,60 0,50 0,37 0,65 1,45 1,5 1,2 1,1 0,95 0,85 1,45 0,12 | 0,10 0,30 0,20 0,20 0,30 0,30 0,30 0,70 0,95 0,85 1,45 0,12 | |||||||||
Примечание. Содержание в сталях Ni, Cu, P и S в таблице не указано.
3.4. Определение величины ферритного зерна
Методы выявления и определения величины зерна при контрольных испытаниях стали регламентированы ГОСТ 5639.
Одним из наиболее точных методов определения величины зерна является измерение среднего условного диаметра зерна методом секущих. Определение обычно проводят либо на матовом стекле микроскопа, либо в окуляре, в который вставлен окулярный вкладыш со шкалой, либо на микрофотографии. Ось шкалы в окулярном вкладыше, или линия, проведенная на микрофотографии, является секущей. Она располагается произвольно. Подсчитываются точки пересечения прямых линий с границами зерен. Если концы линий оканчиваются на самом зерне, а не на границе, то два «конечных» зерна принимают за одно. Производится не менее трех замеров. Затем определяются суммарная длина отрезков (линий) в миллиметрах 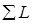 и суммарное число пересечений зерен
и суммарное число пересечений зерен 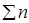 . Диаметр зерна подсчитывается следующим образом. Если используется микрофотография, сделанная при определенном увеличении микроскопа, то
. Диаметр зерна подсчитывается следующим образом. Если используется микрофотография, сделанная при определенном увеличении микроскопа, то
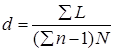 [мм],
[мм],
где 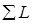 – суммарная длина всех отрезков, мм;
– суммарная длина всех отрезков, мм; 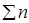 – суммарное число пересечений отрезков секции с границами зерен; N – увеличение микроскопа.
– суммарное число пересечений отрезков секции с границами зерен; N – увеличение микроскопа.
Если подсчет проводится на микрошлифе с помощью окуляра со шкалой, то
 [мм],
[мм],
где 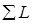 – суммарная длина отрезков шкалы окуляра микроскопа в единицах шкалы;
– суммарная длина отрезков шкалы окуляра микроскопа в единицах шкалы; 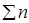 – суммарное число пересечений шкалы с границами зерен; А – цена деления шкалы окуляра при данном увеличении микроскопа.
– суммарное число пересечений шкалы с границами зерен; А – цена деления шкалы окуляра при данном увеличении микроскопа.
Пример. На микрофотографии, сделанной при увеличении в 100 раз (рис. 5), проведены 4 отрезка секущей с длиной L 1 = L 2 = L 3 = 50 мм, L 4 = 48 мм. Суммарная длина отрезков 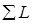 = L 1 + L 2 + L 3 + L 4 = 50 + 50 + + 50 + 48 = 198 мм. Число пересечений отрезков с границами зерен n 1 = 12, n 2 = 11, n 3 = 14, n 4 = 14.
= L 1 + L 2 + L 3 + L 4 = 50 + 50 + + 50 + 48 = 198 мм. Число пересечений отрезков с границами зерен n 1 = 12, n 2 = 11, n 3 = 14, n 4 = 14.
Суммарное число пересечений 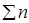 = n 1 + n 2 + n 3 + n 4 = 12 + 11 + 14 + 14 = 51. Вычисляем средний диаметр зерна
= n 1 + n 2 + n 3 + n 4 = 12 + 11 + 14 + 14 = 51. Вычисляем средний диаметр зерна
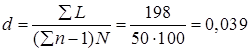 мм.
мм.
3.5. Определение объемной доли перлита
Наиболее объективную оценку структуры по количеству перлита можно получить, применив точечный метод Глаголева.
Теория вероятности показывает, что если на какой-то плоскости имеется определенное количество равномерно расположенных точек, то число точек, находящихся на отдельных участках, будет пропорционально площади этого участка.
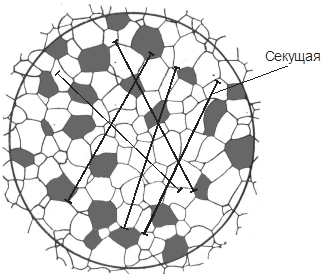
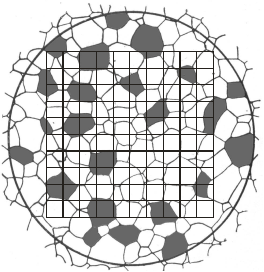
| Рис. 5. Измерение среднего диаметра зерна (ГОСТ 5639) d з = (S LА)/S n: L – суммарная длина отрезков (линий), мм; n – суммарное число пересечений зерен; А – цена деления при данном увеличении | Рис. 6. Определение процентного содержания перлита в стали |
Количество перлита определяют следующим образом. На микроскоп устанавливают окуляр с сеткой, либо наносят сетку на микрофотографию. Подсчитывают число узлов – точек пересечения линий сетки, попавших на перлит (рис. 6). Количественное содержание перлита в исследуемой стали определяется по формуле
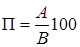 , (14)
, (14)
где П – содержание перлита в стали; А – количество узлов, попавших на перлит; В – общее число узлов в сетке.
Пример. При исследовании ферритно-перлитной стали из 81 точки) на перлит пришлось 25 точек.
Тогда количественное содержание перлита в стали будет
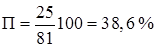
4. Нахождение коэффициентов уравнения предела текучести
Каждый студент после выполнения экспериментальных исследований находит значения семи неизвестных с семью неизвестными коэффициентами при них. Цель данного раздела заключается в определении этих коэффициентов.
Подгруппа, состоящая из двенадцати студентов, получает двенадцать уравнений первого порядка с семью неизвестными.
Так как уравнений больше, чем неизвестных, то получившаяся система несовместна и для неизвестных величин нужны наиболее вероятные значения. Для решения данной системы применим метод регрессионного анализа. Запишем нашу систему в математически удобной форме, что необходимо для правильного ввода информации в программу. Для этого введём обозначения членов уравнения
| В уравнении | sт | sп | Jb r1/2 | %Mn | %Si | %Cr | d– 1/2 | n |
| Обозначения | Bi | Ai 1 | Ai 2 | Ai 3 | Ai 4 | A i5 | A i6 | A i7 |
| Количественное значение | ||||||||
| Размерность |
Соответственно введём обозначения коэффициентов при каждой переменной
| В уравнении | a | K Mn | K Si | K Cr | K y | K перл | |
| Обозначения | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 | x 7 |
Тогда в общем виде уравнение предела текучести запишется как
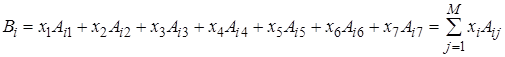 ,
,
где i = 1… N – номер подгруппы студентов, j = 1… M – индекс неизвестного коэффициента.
В данной работе: N = 12 – число подгрупп, M = 7 – число неизвестных в уравнении.
Итак, задача сводится к нахождению коэффициентов (xj, j = 1… M) многочлена, которые называются коэффициентами множественной регрессии и выражают вклад значения каждого из переменных в общую величину функции – предела текучести.
Решение выполняется по методу наименьших квадратов. Основы метода заключаются в следующем.
Если из опыта определяются значения f 1 некоторых функций
j i (x 1, x 2, … xn) (i = 1,2, … m)
неизвестных величин x 1, x 2, … xn, то для определения этих величин необходимо решить систему условных уравнений
j i (x 1, x 2, … xn) – fi = 0 (i = 1,2, … m)
Эта система, вообще говоря, несовместна при (m > n), и для неизвестных величин нужны наиболее вероятные значения. Если ошибки нахождения величин имеют нормальный закон распределения (что обычно допускают), то для наиболее вероятной системы значений неизвестных сумма квадратов отклонений
e i = j i – fi будет наименьшей. Если условные уравнения линейны:
a 1 x 1 + b 1 x 2 + … + l 1 xn = f 1,
a 2 x 1 + b 2 x 2 + … + l 2 xn = f 2,
………………………….
amx 1 + bmx 2 + … + lmxn = fm.
то требование минимума суммы квадратов отклонений приводит к системе линейных нормальных уравнений:
[ aa ] x 1 + [ ab ] x 2 + …[ a l] xn = [ af ],
[ ba ] x 1 + [ bb ] x 2 + …[ b l] xn = [ bf ],
………………………………...
[l a ] x 1 + [l b ] x 2 + …[ll] xn = [l f ].
Для получения k -го нормального уравнения необходимо каждое условное уравнение умножить на коэффициент при xk и все уравнения сложить (В последней системе использовались обозначения Гаусса: вместо 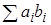 можно записать коротко [ ab ].)
можно записать коротко [ ab ].)
Ниже даны индивидуальные задания для студентов. Полученные результаты суммируются и оформляются на ЭВМ.
 Задание 1
Задание 1


 Задание 2
Задание 2


 Задание 3
Задание 3

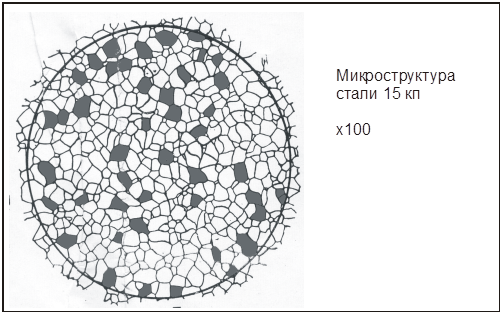
 Задание 4
Задание 4

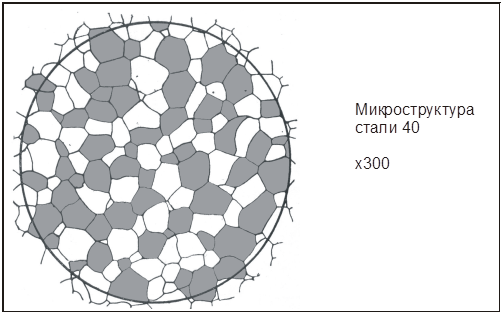
 Задание 5
Задание 5

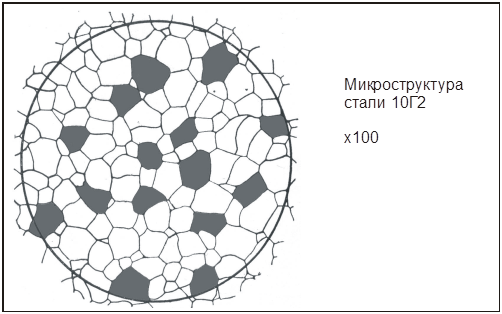
 Задание 6
Задание 6


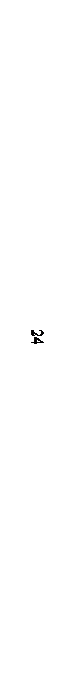 Задание 7
Задание 7

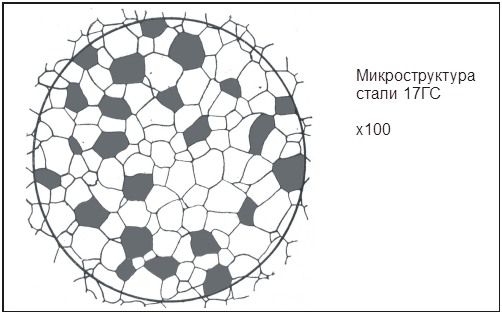
 Задание 8
Задание 8

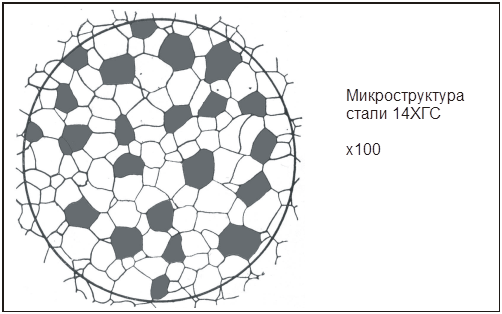
 Задание 9
Задание 9


 Задание 10
Задание 10


 Задание 11
Задание 11

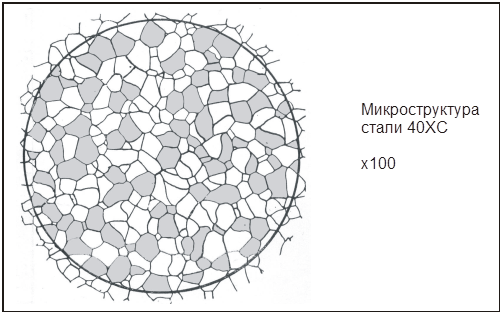
 Задание 12
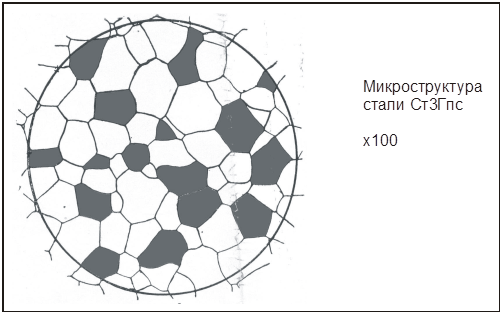
Задание 12

Контрольные вопросы
1. Как ведут расчет ответственных конструкций?
2. Как можно повысить предел текучести сплава?
3. Расшифруйте понятие «вязкость разрушения (трещиностойкость)».
4. В чем сущность силы Пайерлса–Набарро?
5. От чего зависит величина упрочнения растворенными атомами?
6. Какой элемент дает наибольшее упрочнение твердого раствора?
7. В чем сущность упрочнения микроструктурными барьерами?
8. Каков физический смысл коэффициента в уравнении Петча–Холла?
9. Какие виды микроструктурных барьеров имеются в ферритно-перлитных сталях?
10. В чем сущность метода регрессионного анализа?
11. Какие участки характерны для кривой растяжения?
12. Что такое «плотность дислокаций»?
13. К какой группе дефектов относят краевые дислокации?
14. Почему в формулу подсчета плотности дислокации вводят коэффициент вероятности?
15. В чем сущность измерения среднего диаметра зерна феррита методом секущих?
16. Как определяют объемную долю перлита в малоуглеродистой стали?
Количественный анализ уравнения
конструктивной прочности углеродистых сталей
после объемного упрочнения
Методические указания к выполнению лабораторной работы
Редактор Н.В. Городник
Технический редактор Н.В. Гаврилова
Компьютерная верстка В.Ф. Ноздрева
Подписано в печать 16.11.2006. Формат 60´84 1/8. Бумага офсетная. Тираж 100 экз. Уч.-изд. л. 3,72. Печ. л. 4,0. Изд. № 176. Заказ №. Цена договорная
Отпечатано в типографии
Новосибирского государственного технического университета
630092, г. Новосибирск, пр. К. Маркса, 20






