Общая характеристика симплексного метода. Запись задачи линейного программирования для решения симплексным методом;
Заполнение первой симплексной таблицы.
3. Определение оптимальности плана. Алгоритм построения новой симплексной таблицы.
4. Пример перехода к новой симплексной таблице.
Вопрос №1 Общая характеристика симплексного метода. Запись задачи линейного программирования для решения симплексным методом.
Широко используемым на практике методом решения задач линейного программирования является симплексный. Этот метод решения задачи линейного программирования основан на переходе от одного опорного решения к другому, при котором значение целевой функции улучшается (на максимум - увеличивается, на минимум - уменьшается или остается на прежнем уровне), при условии, что данная задача имеет оптимальный план.
При решении задачи симплексным методом можно выделить следующие стадии:
1) приведение задачи к канонической форме и нахождение первоначального варианта допустимого плана;
2) проверка найденного варианта плана на оптимальность (если полученный вариант окажется оптимальным, то решение получено, в противном случае план должен быть улучшен);
3) последовательное улучшение плана в симплексных таблицах до получения оптимального.
Рассмотрим пример записи экономической задачи.
Пример. Коммерческое предприятие, располагающее материально-денежными ресурсами, реализует три группы товаров А, В и С. Плановые нормативы затрат ресурсов на 1 тыс. руб. товарооборота, доход от продажи товаров на 1 тыс. руб. товарооборота, а также объем ресурсов заданы в таблице 1.
Определите плановый объем продажи и структуру товарооборота так, чтобы доход торгового предприятия был максимальный.
Таблица 1 – Исходные данные для решения задачи
| Виды материально-денежных ресурсов | Норма затрат материально-денежных ресурсов на 1 тыс. руб. товарооборота | Объем ресурсов | ||
| А (х1) | В(х2) | С(х3) | ||
| Рабочее время продавцов, чел.-час. | 0,1 | 0,2 | 0,4 | |
| Площадь торговых залов, м2 | 0,05 | 0,02 | 0,02 | |
| Площадь складских помещений, м | ||||
| Доход, тыс. руб. | максимум |
Решение. Запишем математическую модель задачи: определить значения переменных: х1, х2, х3, удовлетворяющих следующей системе ограничений:
0,1х1 + 0,2х2 + 0,4х3 ≤ 1100 – по рабочему времени продавцов, чел.-час.
0,05 х1 +0,02 х2 + 0,02 х3≤ 120 – по площади торговых залов, м2
3 х 1 +х2 + 2 х3 ≤ 8000 - по площади складских помещений
XI ≥0, X2 ≥0, X3 ≥0 – условие неотрицательности переменных
и обеспечивающих максимальное значение целевой функции
Z = 3х 1+5х 2+4х 3 ->max
Чтобы решить данную задачу линейного программирования симплексным методом, она должна быть представлена в канонической форме, система ограничений приведена к единичному базису, свободные члены уравнений должны быть неотрицательны.
Для построения первого опорного плана систему неравенств приведем к канонической форме путем введения дополнительных (базисных) переменных х 1, х 2, х 3. В том случае, если неравенство имеет знак ≤, базисная переменная добавляется в неравенство со знаком «+», если знак неравенства ≥, базисная переменная добавляется со знаком «-». В нашем примере все неравенства со знаком ≤, следовательно, базисные переменные х4, х5 и х6 добавляются со знаком «+»:
0,1х1+0,2х2+0,4хз+х4 = 1100
0,05х1+0,02х2+0,02х3+х5 = 120
3х1+х2+2х +х6= 8000
XI ≥0, X2 ≥0, X3 ≥0, X4 ≥0, X5 ≥0, X6 ≥0
Z = 3 х 1+ 5х 2 + 4х 3 + 0х 4 + 0х 5 + 0х 6 ->max
Составим первую симплексную таблицу. Она представляет собой форму выражения первого опорного плана. Коэффициенты стоящие в Z-строке, показывают как изменяется значение целевой функции при единичном изменении соответствующей свободной переменной. И называются эти коэффициенты оценкой или индексом этой свободной переменной. А сама строка Z называется индексной или оценочной.
Вопрос №2 Заполнение первой симплексной таблицы.
1. В первом столбце перечисляют базисные переменные.
2. Во второй столбец записывают оценки базисных переменных, указанные в целевой функции.
3. В третьем столбце указывают свободные члены.
4. В остальных столбцах таблицы записывают коэффициенты при свободных переменных по соответствующим уравнениям.
5. Над рабочей частью таблицы перечисляют свободные переменные.
6.Сверху над свободными переменными помещают оценки свободных переменных, указанные в целевой функции. Над столбцом свободных членов записывают свободный член целевой функции (если таковой имеется) с противоположным знаком.
7. Оценки Z – строки рассчитывают по формуле:
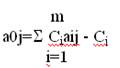
где j=1, 2,…,n
aij – коэффициенты j –ого столбца,
Ci - коэффициенты при базисных переменных в уравнении Z,
Cj - коэффициенты при свободных переменных в уравнении Z.
Далее представлен пример заполнения первой симплексной таблицы в соответствие с использованием данных канонической системы уравнения.
0,1 х1+0,2х2+0,4хз+х4 = 1100
0,05х1+0,02х2+0,02х3+х5 = 120
3х1+1*х2+2х3 +х6= 8000
XI ≥0, X2 ≥0, X3 ≥0, X4 ≥0, X5 ≥0, X6 ≥0
Z = 3 х 1+ 5х 2 + 4х 3 + 0х 4 + 0х 5 + 0х 6 ->max
Таблица 2 – Заполнение первой симплексной таблицы (опорного плана)
| Базисные переменные | Cj | ||||
| Ci | ai0 | X1 | X2 | X3 | |
| X4 | 0,1 | (0,2) | 0,4 | ||
| X5 | 0,05 | 0,02 | 0,02 | ||
| X6 | |||||
| Z | -3 | -5 | -4 |
| Базисные переменные | |
| Коэффициенты при базисных переменных в целевой функции | |
| Свободные члены уравнения | |
| Свободный член целевой функции (число без переменной, заносится с противоположным знаком) – если отсутствует – принимается равным 0 | |
| Свободные переменные | |
| Коэффициенты перед свободными переменными в целевой функции (оценки свободных переменных) | |
| Коэффициенты при соответствующих переменных в системе уравнений | |
| Коэффициент z-строки = 0*1100+0*120+0*8000-0 | |
| -3 | Коэффициент z-строки = 0*0,1+0*0,05+0*3-3 |
| -5 | Коэффициент z-строки = 0*0,2+0*0,02+0*1-5 |
| -4 | Коэффициент z-строки = 0*0,4+0*0,02+0*2-4 |
Вопрос №3 Определение оптимальности плана. Алгоритм построения новой симплексной таблицы
В симплексных таблицах формальным признаком оптимальности является содержание оценочной строки (Z-строки).
| Ключевая теорема симплексного метода (Z на максимум): Если после выполнения очередной итерации: 1) найдется хотя бы одна отрицательная оценка, а в столбце, где она стоит, есть хотя бы один положительный элемент, то опорное решение можно улучшить, выполнив следующую итерацию; 2) найдется хотя бы одна отрицательная оценка, столбец которой не содержит положительных элементов, то функция Z неограниченна в области допустимых решений (Zmax ®+¥); 3) все оценки окажутся неотрицательными, то достигнуто оптимальное решение. |
Согласно данной теореме переход к следующей симплексной таблице осуществляется следующим образом:
1. Просматриваются оценки Z - строки. Если они все неотрицательны, то получено оптимальное решение при решении на максимум целевой функции, если все оценки £ 0, то получено оптимальное решении при решении на минимум целевой функции.
2. Если оптимальное решение не получено, то выбирается разрешающий столбец по наибольшей по абсолютной величине отрицательной оценке Z - строки при решении на максимум и по наибольшей положительной оценке при решении на минимум целевой функции.
3. Составляются симплексные отношения - отношения свободных членов к положительным коэффициентам разрешающего столбца. Минимальное из этих отношений (min íai 0/ aipý) определит разрешающую строку. Коэффициент, находящийся на пересечении разрешающей строки и разрешающего столбца, называется разрешающим элементом.
Если в разрешающем столбце нет ни одного положительного коэффициента, то задача не имеет решения по причине неограниченности целевой функции (Zmax®+¥,Zmin®-¥).
4. Осуществляется переход к новой таблице, где базисная переменная заменяется на свободную, соответствующую разрешающему столбцу.
5. Бывший разрешающий элемент заменяется обратным по величине (1/ аqp).
6. Все остальные элементы бывшего разрешающего столбца делятся на разрешающий элемент и меняют знаки на противоположный.
Если в бывшем разрешающем столбце в какой-то строке стоял “0”, то эта строка переносится в следующую таблицу без изменений.
7. Все остальные элементы бывшей разрешающей строки делятся на разрешающий элемент.
Если в бывшей разрешающей строке в каком-то столбце стоял “0”, то этот столбец переносится в следующую таблицу без изменений.
8. Остальные элементы таблицы пересчитываются по правилу “прямоугольника”:
9. Осуществляется контроль за правильностью расчетов для элементов Z-строки.
10. Если ошибок нет, то алгоритм повторяется с пункта 1.
Вопрос №4 Пример перехода к новой симплексной таблице.
Таблица 3 – Симплексная таблица (исходное опорное решение)
| Базисные переменные | Cj | Симплексные отношения | ||||
| Ci | ai0 | X1 | X2 | X3 | ||
| X4 | 0,1 | (0,2) | 0,4 | 5500← | ||
| X5 | 0,05 | 0,02 | 0,02 | 6000 | ||
| X6 | 8000 | |||||
| Z | 0 | -3 | -5↑ | -4 |
Исходное опорное решение записывается по столбцу свободных членов. Та как свободным переменным в указанном столбце не соответствуют свободные члены, то Х1=0, Х2=0, Х3=0. Базисным переменным соответствуют определенные свободные члены Х4=1100, Х5=120, Х6=8000. Следовательно, опорное решение записывается так Хоп.(0,0,0,1100,120,8000). Zmax= 0.
Так как мы решаем задачу на максимум, для достижения оптимального решения все числа в Z-строке должны быть неотрицательными. По этому опорный план не является оптимальным.
Для перехода к следующей таблице выбираем разрешающий столбец (при решении на максимум по наибольшей по модулю отрицательной оценке (-5)). Далее считаем симплексные отношения: 1100/0,2 = 5500, 120/0,02 = 6000, 8000/1= 8000.
В первой симплексной таблице нашего примера все коэффициенты оценочной строки отрицательны. Следовательно, согласно теореме, план (на максимум целевой функции) не является оптимальным и требует улучшения. По наименьшему симплексному отношению выбираем разрешающую строку и переходим ко второй симплексной таблице (таблица 4).
Таблица 4 – Вторая симплексная таблица
| Б.П. | Cj | ai0/aip | ||||
| Ci | ai0 | X1 | X4 | X3 | ||
| X2 | 5500* | 0,5* | 5* | 2* | ||
| X5 | 10* | (0,04)* | -0,1* | -0,02* | 250< | |
| X6 | 2500* | 2,5* | -5* | 0* | ||
| Z | 27500* | -0,5* | 25* | 6 * |
Во второй симплексной таблице свободная переменная разрешающего столбца (Х2) переходит на место базисной переменной разрешающей строки (Х4), а Х4 – на место Х2. далее в разрешающем столбце на месте бывшего разрешающего элемента записываем обратную величину: 1 / (0,2) = 5*. Все остальные элементы бывшего разрешающего столбца делим на разрешающий элемент и записываем с противоположным знаком: 0,02/ (0,2) * (-1) = -0,1*, 0,1/(0,02) * (-1) = -5*, 5/(0,02)*(-1) = 25*. Для нахождения остальных элементов разрешающей строки необходимо коэффициенты бывшей разрешающей строки разделить на разрешающий элемент: 5500*=1100/(0,2), 0,5*=0,1/(0,2) и т.д.
Все остальные элементы таблицы находятся по правилу прямоугольника по следующей схеме: бывший коэффициент – (коэффициент разрешающей строки * коэффициент разрешающего столбца)/разрешающий элемент. На пример:
- 0,02*=0,02 – (0,02*0,4)/ (0,2), 6*=-4-(-5*0,4)/ (0,2) и т.д.
Оценки Z-строки в таблице 4 указывают на неоптимальность плана, так как имеется отрицательный элемент. Он единственный, поэтому в качестве разрешающего столбца выбирается столбец с отрицательным элементом. Далее весь алгоритм повторяется снова. В результате получаем следующую сиплексную таблицу (таблица 5).
Таблица 5 – Последняя симплексная таблица
| Б.П. | Cj | ai0/aip | ||||
| Ci | ai0 | X5 | X4 | X3 | ||
| X2 | 12,5 | 6,25 | 2,25 | |||
| X1 | -2,5 | -0,5 | ||||
| X6 | -62,5 | 1,25 | 1,25 | |||
| Z | 12,5 | 23,75 | 5,75 |
Оптимальный план можно записать так: Х1=250, Х2=5375, Х3=0, Х4=0, Х5=0, Х6=1875 или Хопт.(250, 5375, 0, 0, 0, 1875); Zmax=27 625 тыс.руб.
Следовательно, необходимо продавать товаров первой группыХ1= 250 ед., а второй группы Х2= 5375 ед. При этом торговое предприятие получает максимальный доход в размере 27 625 тыс. руб. Товары группы С не реализуются.
В оптимальном плане среди базисных переменных находится дополнительная переменная Х6. Это указывает на то, что ресурсы третьего вида (площадь складских помещений) недоиспользована на 1875 м2, так как переменная Х6 была введена в третье ограничение задачи, характеризующее собой использование складских помещений этого ресурса.






