Представьте себе: на реакторной установке с ВВЭР, находящейся в подкритическом состоянии, которое обеспечивается за счёт величины стояночной концентрации борной кислоты (Сст), начинается процедура пуска. То есть система борного регулирования переключается в режим подпитки первого контура чистым дистиллатом с заданным постоянным расходом Gп. Требуется определить, сколько времени должна работать система подпитки в таком режиме до момента, когда концентрация борной кислоты в контуре снизится до заданного значения С1 (в частности, это может быть величина пусковой критической концентрации Сп).
Эта задача может быть решена чисто аналитическим методом. В соответствии с закономерностью изменения концентрации борной кислоты при подпитке контура чистым дистиллатом текущее значение этой концентрации:
, (23.3.1)
где: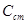 
, г/кг – начальное (стояночное) значение концентрации борной кислоты;
g, кг/м3 – плотность воды при давлении и средней температуре в активной зоне во время пуска реактора;
V, м3 – объём теплоносителя в первом контуре при данном уровне его в компенсаторе давления;
Величину расхода подпитки первого контура дистиллатом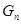 
в эту формулу следует подставлять в единицах системы СИ – кг/с. Если желательно пользоваться более привычной в эксплуатационных условиях внесистемной размерностью расхода подпитки (т/час), в формулу следует добавить переводной множитель:
. (23.3.1-а)
Разумеется, время t и во втором случае следует подставлять в [ с ], что хотя и несложно для перевода из [ мин ] или [ час ], но довольно нудно. Поскольку время работы подпиточных насосов до достижения критичности реактора в различных условиях пусков имеет порядок нескольких часов или десятков часов, для того, чтобы подставлять в формулу время в [ ч ], расчётная формула должна иметь вид:
(23.3.1-б)
Из (23.3.1-б) следует, что время снижения концентрации борной кислоты в контуре от стояночного (Сст) до произвольного значения С1 должно составить
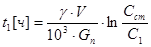. (23.3.2)
По этой формуле легко вычисляется время работы системы подпитки с заданным расходом Gп до момента достижения пусковой критической концентрации борной кислоты в воде первого контура.
Пример. Стояночная концентрация борной кислоты в контуре перед пуском ВВЭР-1000 была равна Сст = 12.4 г/кг, а расчётное значение пусковой концентрации Сп = 8.2 г/кг. Требуется определить, какое время потребуется для достижения пусковой концентрации борной кислоты в контуре при расходе подпитки Gп = 20 т/ч при давлении теплоносителе в первом контуре р1 = 15.0 МПа и средней температуре его t = 290 оС. Объём теплоносителя в первом контуре V = 325 м3.
Решение
1. Из Таблиц теплофизических свойств воды и водяного пара (С.Л. Ривкин, А.А. Александров, М., «Энергия», 1989) находится удельный объём воды при р1 = 15 МПа и t = 290 оС: v = 0.0013410 м3/кг, и, следовательно, плотность воды
кг/м3.
2. Подставляя все известные данные в формулу (23.3.2), имеем:
ч.
Та же задача, если Вас не слишком заботит точность вычислений, может быть решена чисто графическим методом. В распоряжении операторов всегда имеются заранее рассчитанные графики снижения концентрации борной кислоты при подпитке первого контура дистиллатом с различными расходами (семейство графиков на рис.22.2). Для нахождения искомого времени подпитки по такому графику следует:
а) Отметить на оси ординат точку, соответствующую исходной (стояночной) концентрации борной кислоты (Сст = 12.4 г/кг), провести через неё горизонтальную прямую до пересечения с экспонентой Gп = 20 т/ч и найти абсциссу этой точки (tст);
б) Таким же образом определить абсциссу точки экспоненты Gп = 20 т/ч, соответствующую пусковой концентрации борной кислоты (Сп = 8.2 г/кг), - tп;
в) Искомое время работы системы подпитки с заданным расходом Gп равно
.
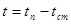Сказанное качественно иллюстрируется следующим графиком:
С(t)
Экспонента С(t) при заданном расходе подпитки Gп
Cст
Сп t – время снижения концентрации борной кислоты
от значения Сст до значения Сп
0 t, ч
tст tп – время снижения концентрации от 16 г/кг до Сп
время снижения концентрации борной кислоты от 16 г/кг до Сст
Рис.23.3. Использование расчётных графиков водообмена при подпитке первого контура дистиллатом с заданным расходом для определения времени работы подпиточных средств для снижения концентрации борной кислоты в контуре от стояночного до пускового значения.
Преимущество аналитического расчёта времени t состоит в точности определения времени пуска (плюс-минус несколько минут), в то время как графический метод даёт недостаточную точность (± 0.5 ч), поскольку экспоненты графиков обычно рассчитываются для рабочих параметров теплоносителя, а не для конкретных его параметров в условиях пуска первого контура.
Планируя пуск, можно существенно сэкономить во времени на эту операцию, если, например, предусмотреть снижение концентрации борной кислоты в два этапа: от 12.4 г/кг до 8.5 г/кг при повышенном расходе подпитки (например, Gп1 = 50 т/ч), а оставшийся интервал от 8.5 до 8.2 г/кг – при сниженном расходе (например,при расчётном значении безопасного пускового расхода Gп2 = 10 т/ч). В этом случае время снижения концентрации до 8.5 г/кг:
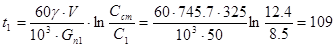мин,
а время заключительного этапа подпитки - до снижения концентрации борной кислоты от 8.5 г/кг до пускового значения Сп = 8.2 г/кг:
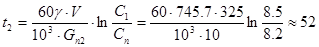мин,
то есть потребное на операцию пуска суммарное время t = 109 + 52 = 161 мин» 2.68 ч.
