При водообмене
Дифференциальное уравнение баланса количества борной кислоты в первом контуре с объёмом воды в нём V м3 с плотностью воды g кг/м3 и текущим значением концентрации борной кислоты С(t) г/кг имеет вид:
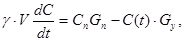(22.2.1)
где: Сп, г/кг – концентрация борной кислоты в подпиточной воде (в баке борного регулирования);
Gп, кг/с – массовый расход, обеспечиваемый системой подпитки I контура;
Gу, кг/с – расход утечек (дренажа) первого контура.
Здесь первое слагаемое правой части (22.2.1) – скорость увеличения массы борной кислоты в первом контуре, приходящей из системы борного регулирования через систему подпитки, а второе – скорость убыли массы борной кислоты из I контура за счёт утечек из первого контура.
В стационарном режиме работы I контура, когда расход утечек в точности восполняется расходом подпитки I контура (Gп = Gу), а именно этот режим строго соблюдается на практике (иначе в контуре давление теплоносителя либо растёт при Gп > Gу, либо падает при Gп < Gу), и поэтому уравнение (22.2.1) с учётом этого условия будет:
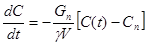. (22.2.2)
Если в некоторый момент времени t = 0, принимаемый за момент начала отсчёта переходного процесса, величина концентрации борной кислоты в контуре была Со, то решение уравнения (22.2.2) при таком начальном условии будет:
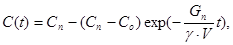(22.2.3)
- то есть изменение концентрации борной кислоты в I контуре в самом общем случае водообмена происходит во времени по экспоненциальному закону.
Для практика интересны два частных случая характера изменения концентрации борной кислоты, а именно:
а) Если начальное значение концентрации Со = 0 (что бывает при первом вводе борной кислоты в воду первого контура), то:
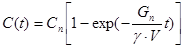, (22.2.4)
то есть при первичном вводе борной кислоты в контур нарастание концентрации борной кислоты проиходит по экспоненциальному закону, причём для конкретной АЭУ, работающей в режиме с фиксированными параметрами, темп нарастания концентрации определяется только величиной концентрации кислоты в баке борного регулирования (Сп) и производительностью подпиточных насосов первого контура (Gп).
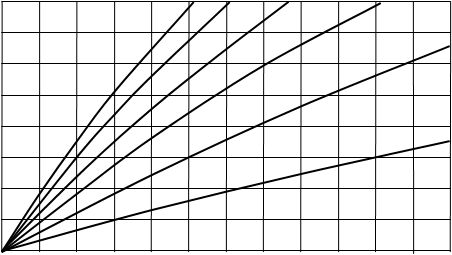
Чем больше подача подпиточных средств, тем выше темп нарастания концентрации борной кислоты в воде I контура. Чем выше концентрация борной кислоты в подпиточной воде, тем выше скорость роста концентрации кислоты в I контуре. Характер роста концентрации кислоты в контуре показан на рис.22.1.
Gп= 60 50 40 30
16
С(t), г/кг
10 т/час
0 50 100 150 200 250 t, мин
Рис.22.1. Рост концентрации борной кислоты при первичном вводе её в первый контур
(концентрация вводимого раствора – 40 г/кг)
б) Случай, когда Сп = 0 (то есть при разбавлении теплоносителя I контура чистым дистиллатом):
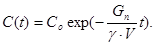(22.2.5)
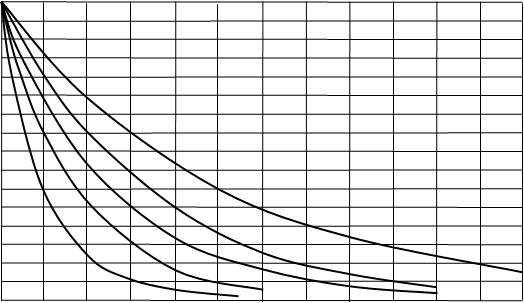
Как видим, и в этом случае (рис.22.2) падение величины концентрации борной кислоты в воде I контура происходит по экспоненциальному закону, задаваемому в конкретной АЭУ только производительностью подпиточных средств (равной расходу протечек первого контура).
16
С(t), г/кг
0 10 20 30 40 50 t, час
Рис.22.2. Снижение концентрации борной кислоты в реакторе ВВЭР-1000 при расходах подпитки
первого контура чистым дистиллатом (сверху вниз) – 10, 15, 20, 30, 50 т/час.
Пользуясь подобными графиками (а они обязательно входят в состав рабочей документации оператора РУ), можно решать два типа практических задач:
- по заданным величинам начальной концентрации борной кислоты С1 и массового расхода системы подпитки Gп рассчитывать величину концентрации борной кислоты С(t), которая будет иметь место через время t работы системы подпитки в таком режиме;
- по заданным величинам начальной и конечной концентраций борной кислоты в теплоносителе 1 контура определять время работы подпиточных средств с заданным расходом;
- по заданной пусковой концентрации борной кислоты и положению рабочей группы ОР СУЗ в момент пуска в заданный момент кампании определять величину допустимого расхода подпиточных средств при подпитке первого контура чистым дистиллатом, обеспечивающего безопасную величину скорости высвобождения положительной реактивности при пуске реактора.
*) О том, как решаются задачи последнего типа, будет сказано немного позднее.
