Второй замечательный предел.

ЭЛЕМЕНТЫ АНАЛИЗА

Л е к ц и я 10

ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ

ПЛАН

Первый замечательный предел.

Второй замечательный предел.

3. Раскрытие неопределенностей и .

Вычисление пределов.

Первый замечательный предел.

При вычислении пределов выражений, содержащих тригонометрические функции, часто используют предел

, (1)

называемый первым замечательным пределом. Читается так: предел отношения синуса к его аргументу равен единице, когда аргумент стремится к нулю.

Обратим внимание, что при аргументе, стремящемся к нулю, числитель и знаменатель тоже стремятся к нулю, т.е. мы имеем неопределенность вида . Таким образом, вспоминая предыдущую лекцию, числитель и знаменатель являются бесконечно малыми функциями при . Предел их отношения равен единице, следовательно, функции sinx и x являются эквивалентными б.м. функциями при :

при , тогда, согласно теореме о замене в пределе на эквивалентную величину, при вычислении предела можно заменить на .

Пример. Найти .

· Решение: Имеем неопределенность вида . Теорема о пределе дроби неприменима. Обозначим ; тогда при и , поэтому

Можно решить без замены на новую переменную: при .

Второй замечательный предел.

Рассмотрим числовую последовательность . Запишем члены этой последовательности, давая n последовательно значения 1, 2, 3, …

Будем иметь: при n=1 : при n=2 ; при n=3 и т. д.

Подставляя последовательно n, можно убедиться, чтодля 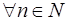выполняются неравенства: , то есть последовательность ограничена снизу и сверху, при увеличении n членыпоследовательности увеличиваются, то есть данная последовательность монотонно возрастает. По известной теореме Вейерштрасса ограниченная монотонная последовательность имеет предел.

Последовательность , , имеет предел, обозначаемый буквой :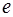

. (2)

Число 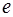иррациональное, его приближенное значение равно 2,72 ( 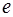= 2,718281828459045...). Число 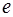принято за основание натуральных логарифмов: логарифм по основанию 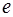называется натуральным логарифмом и обозначается , т. е. .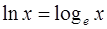

Число 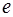есть предел последовательности. Аргументом является натуральное число. Можно доказать, что для любого вещественного аргумента x существует предел функции:

. (3)

Обратим внимание на неопределенность, возникающую при подстановке в функцию предельного значения аргумента x. При возникает неопределенность вида . Второй замечательный предел имеет другую формулировку с аналогичной неопределенностью, а именно:

. (4)

Действительно, если в равенстве (3) положить ( при ), оно запишется в виде (4).

Пределы (3) и (4) называются вторым замечательным пределом.

Они широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием 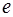. Функция называется экспоненциальной, употребляется также обозначение .

Пример: Найти .

Решение: Обозначим , очевидно, 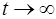при . Имеем

.

3. Раскрытие неопределенностей и .

При возникает неопределенность вида . Для вычисления пределов в

этом случае используется основное свойство дроби, а именно: дробь не изменится, если числитель и знаменатель дроби умножить или разделить на одно и то же число или выражение. Рассмотрим пример.

Пример: .

Если при вычислении предела иррациональной функции возникает неопределенность вида , то для получения ответа тоже используется основное свойство дроби. Рассмотрим примеры.

Пример:

Пример:

Вычисление пределов.

Для раскрытия неопределённостей вида часто бывают полезным применять принцип замены бесконечно малых эквивалентными и другие свойства эквивалентных бесконечно малых функций. Как известно, при , при . Приведем еще примеры эквивалентных б.м.ф.