Введение
Первое теоретическое обоснование явления гидравлического удара были даны Н.Е.Жуковским. Опыты, проведенные им на Алексеевской водокачке, снабжавшей в те годы (1898 г.) водой Москву, на водопроводе длиной 760 м, показали редкое совпадение расчетов по теоретической формуле с данными эксперимента без введения каких-либо поправочных коэффициентов.
Разработанная Н.Е.Жуковским теория гидравлического удара получила широкое признание и распространение как у нас, так и за рубежом.
Неустановившееся течение жидкости
В жестких трубах
Неустановившееся течение жидкости это такое течение, все характеристики которого (или некоторые из них) изменяются во времени в точках рассматриваемого пространства.
В общем случае неустановившегося течения давление и скорость зависят как от координат, так и от времени:
Р = f (x, y, z, t)
Q = f (x, y, z, t)
Примером неустановившегося течения жидкости могут служить постепенное опорожнение сосуда через отверстие в дне.
 |
Так как неустановившееся течение жидкости в общем случае является достаточно сложным, то мы ограничимся здесь лишь основным частным случаем, с которым приходится сталкиваться в технике, - неустановившемся течением абсолютно несжимаемой жидкости в жесткой трубе постоянного сечения и в трубопроводе, составленном из ряда последовательно соединенных труб разных диаметров. Стенки труб при этом будем предполагать абсолютно жесткими.
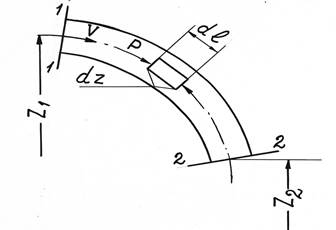
Рисунок 1. Схема неустановившегося течения в трубе.
Возьмем трубу длиной 
и диаметром d, произвольно расположенную в пространстве (рисунок 1), и обозначим нивелирные высоты начального (1-1) и конечного (2-2) ее сечений соответственно через Z1 и Z2. Пусть в этой трубе движется жидкость с ускорением, которое в общем случае может быть переменным по времени и равным
j = 
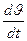(1)
Очевидно, что в данный момент времени скорость 
и ускорение j являются одинаковыми для всех поперечных сечений трубы.
Потерями энергии на трение вначале будем пренебрегать, а распределение скоростей по сечениям будем считать равномерным.
Выделив из движущегося в трубе объема жидкости элементарный цилиндрический объем длиной dl и площадью основания dS (рисунок 1), составим уравнение его движения.
Проектируя силы давления и силу тяжести на направление касательной к оси трубы, (учитывая, что р есть функция не только l, но и t) проведя математические преобразования, получим
(2)
или
, (3)
где
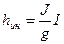(4)
Полученное уравнение сходно с уравнением Бернулли для относительного движения в трубопроводе постоянного сечения, а член 
также называется инерционным напором, однако, путать с 
не следует, так как они имеют разный смысл. Величина , как это видно из уравнения (30), представляет собой разность удельных потенциальных энергий жидкости в сечениях 1-1 и 2-2 в данный момент времени, обусловленную ускорением (или торможением) потока жидкости в трубе. При ускорении эта разность положительна, т.е. удельная энергия жидкости вдоль потока уменьшается, а при торможении – отрицательна, что означает увеличение удельной энергии жидкости от сечения 1-1 к сечению 2-2.
При наличии гидравлических потерь энергии в трубе (местных и на трение) они должны быть записаны в правой части уравнения (3):
(5)
Уравнение (5) справедливо лишь для трубы постоянного сечения. Если же трубопровод состоит из нескольких участков с разными площадями сечений 
, то очевидно, что инерционный напор для всего трубопровода должен быть найден как сумма инерционных напоров для каждого участка. При этом соответствующие ускорения определяются из следующих уравнений, представляющих собой результат дифференцирования уравнений расхода по времени,
Кроме того, как это следует из приведенных выше энергетических соображений, в этом случае следует учесть скоростные напоры в начальном и конечном сечений трубопровода.
Вывод по первому вопросу
Таким образом, уравнение неустановившегося течения жидкости между сечениями c учётом инерции жижкостиимеет вид
(6)
Физическая сущность гидравлического удара
По Н.Е. Жуковскому
Гидравлическим ударом называется повышение или понижение гидродинамического давления в напорном трубопроводе, вызванное изменением во времени (в некотором сечении трубопровода) величины и скорости движения жидкости.
В соответствии со схемой, если мы имеем трубопровод, на конце которого установлен кран «К», то жидкость, находящаяся в трубопроводе, будучи остановлена закрытием крана. Благодаря своей инерции окажет большое давление на закрытый кран.
Если при рассмотрении такого явления пренебрежем сжимаемостью жидкости и деформируемостью стенок в трубопроводе, то при этом получим в трубопроводе так называемый «абсолютно жесткий» удар, что как показывает опыт, вовсе не отвечает действительности.
На характер явления гидравлического удара оказывает большое влияние сжимаемость стенок трубопровода соответствующим образом деформироваться с изменением гидравлического давления в трубопроводе при закрытии или открытии крана получается «упругий удар». Качественно отличающийся от «абсолютно жесткого» удара. В случае «упругого удара» давление вдоль трубопровода распространяется волнами, причем эти волновые явления сказываются весьма резко выраженными, и с ними нельзя не считаться при изучении гидравлического удара.
Рассмотрим явление гидравлического удара в трубах по теории Н.Е. Жуковского. Представим себе трубу длиной L и одинакового диаметра d, присоединенную к большому напорному резервуару и имеющую на конце затвор (например, пробковый кран рисунок 2)
 |
Рисунок 2. Схема возникновения гидравлического удара
Если какой – либо момент времени быстро закрыть кран «К», то вся движущаяся в трубе со скоростью 
масса жидкости должна внезапно остановиться. В результате такого резкого изменения скорости кинематическая энергия этой массы преобразуется в энергию давления, которая у крана «К» может достичь весьма значительной величины.
Так как жидкость и материал трубы все же обладают упругостью, то отмеченное повышение давления, сжатие жидкости и увеличение ее плотности за некоторый промежуток времени 
вызовут расширение упругих стенок трубы в форме вздутия до некоторого диаметра d1, указанного на схеме пунктирными линиями.
Остановка жидкости и повышение давления происходит относительно постепенно от слоя к слою. Поэтому в область вздутия вмещается притекающая дополнительная масса жидкости, отчего объемный удельный вес жидкости в этой области получает новое значение.
По мере поступления этой жидкости, деформация вздутия распространяется от крана «К» по направлению к резервуару в виде волны повышенного давления с некоторой весьма значительной скоростью «С», которую Н.Е.Жуковский назвал скоростью распространения ударной волны.
Если трубопровод и жидкость по длине однородны, то скорость распространения ударной волны «С» будет постоянна. В таком случае волна повышенного давления до резервуара дойдет за промежуток времени
(7)
При значительной вместимости резервуара и большой массе жидкости в нем по сравнению с массой жидкости в трубопроводе явление гидравлического удара не оказывает существенного влияния на уровень и состояние жидкости в напорном резервуаре. Поэтому в конце времени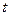 
подхода ударной волны к входному отверстию трубопровода вся жидкость в трубопроводе окажется на мгновенье сжатой. Следовательно, через время 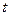в сечении 
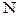возникает положение, при котором в резервуаре давление жидкости будет меньше, чем в трубопроводе. При таких условиях равновесие в сечении невозможно. Поэтому начинается перемещение жидкости из трубопровода в резервуар (из области большого давления в область меньшего) и понижение давления в трубопроводе, которое будет распространяться в сторону крана «К» с той же скоростью «С», снижая волну повышенного давления.
Таким образом, волна повышенного давления, дойдя, до входного отверстия, отразится, переменив знак с положительного на отрицательный.
Время пробега прямой и обратной (отраженной ударных волн) составляет длительность фазы гидравлического удар.
(8)
Дойдя до крана «К», отраженная волна в свою очередь отразится и распространится с той же скоростью по направлению к выходному отверстию. Затем явление повторяется с чередующими один за другим периодическими гидравлическими ударами.
При рассмотрении гидравлического удара полезно иметь в виду следующую аналогию. Представим себе обычную спиральную пружину, имеющую достаточно большую длину. Положим, что эта пружина падает на горизонтальную плоскость. Очевидно, до момента, когда пружина еще не коснулась этой плоскости, распространение между витками пружины будут всюду одинаковыми. После того, как пружина коснулась горизонтальной плоскости, получим картину, представленную на рис. 3: ниже подвижной границы М-М, перемещающейся вверх с некоторой скоростью «С», расстояние между витками пружины относительно малы (эта область будет соответствовать области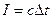 
, рассмотренной выше).
 |
Рисунок 3. К пояснению гидравлического удара
Гидравлический удар, являющийся одним из видов неустановившегося движения жидкости может возникнуть:
при быстром перекрытии сечения трубопровода при подаче по нему жидкости;
при внезапной остановке насоса, ведущего перекачку жидкости по трубопроводу;
при резком изменении режима работы насосной установки, ведущей перекачку жидкости по трубопроводу.
Найдем соответствующие расчетные зависимости для величины 
и С.
Вывод по второму вопросу
Из всего сказанного видно, что явление гидравлического удара характеризуется следующими двумя основными величинами:
1. приращением давления «», дающим величину гидравлического удара;
2. скоростью «С», т.е. скоростью распространения ударной волны.
