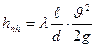В результате формула (7) имеет вид

 

(9)

 

это так называемая формула Дорси – Вейсбаха

Поскольку для круглых труб d=4r, то из уравнения (9) можно получить

 

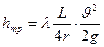(10)

 

Формулы (9) и (10) широко используется при определении потерь напора. Формулу 10 применяют главным образом при расчетах открытых потоков, напорных.

Последние исследования показали, что на потери напора, помимо скорости, влияют и другие факторы (вязкость жидкости, форма и размеры живого сечения, состояние стенок), не учитываемые этими формулами. В настоящее время в формулах Шези и Дарси-Вейсбаха коэффициенты c и λ становятся в косвенную зависимость от всех этих факторов.

Потери напора по длине трубопровода можно определить по формуле Лейбензона, которая получена путем преобразования формулы Дарси-Вейсбаха

 

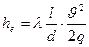
Ввиду того, что , то можно в формуле Дарси-Вейсбаха ввести значения скорости и коэффициента гидравлического сопротивления .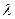

Так как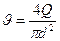

то коэффициент гидравлического сопротивления λ по формуле Блазиуса

 

=

 

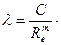
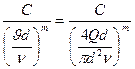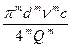
где коэффициенты с и m установлены экспериментально.

 

Подставляя полученные значения в формулу Дарси-Вейсбаха, получим:

 

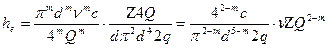
Обозначим 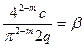тогда

 

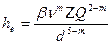; (11)

 

Это и есть формула Лейбензона.

 

Для трубопровода определенного диаметра, при значение 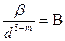формула примет вид

 

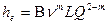(12)

 

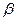и 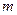коэффициенты, учитывающие режим движение жидкости

 

0,0247 – при турбулентном режиме.

 

Коэффициенты:

m=0,21 – для оцинкованных труб

m=0,22 – для труб с внутренним эмалевым покрытием.

Так для полевых трубопроводов:

 

ПМТ-100 и ПМТП-100 В=1/14000

ПМТ-150 и ПМТП-150 В=1/90000

ПМТБ-200 В=1/540000

Вывод по второму вопросу

Полученные зависимости для определения гидравлических потерь дают возможность проводить гидравлические расчёты сложных гидравлических систем, таких как полевые трубопроводы.

3. График Никурадзе..

При движении реальной жидкости по трубопроводу происходит потеря удельной энергии движущейся жидкости, определяемой по формуле. Дарси-Вейсбаха (9).

В указанной формуле коэффициент гидравлического сопротивления (l) являются одной из основных величин и от правильного определения значения его зависит результат многих гидравлических расчетов. Недооценка значения этого коэффициента может привести к труднопоправивым последствиям: неправильно могут быть подсчитаны расходы, мощность двигателя, ошибка в определении числа насосных станций и их расстановка на трассе ПМТ, что может привести к срыву выполнения задачи по подаче войскам горючего и т.п.

В основном коэффициент l зависит от режима движения и от степени шероховатости трубопровода. Режим движения жидкости характеризуется числом Рейнольдоса, а шероховатость трубопровода- относительной шероховатостью.

Выяснению вопроса о влиянии различных факторов на величину коэффициента l посвящено весьма большое число экспериментальных и теоретических работ.

Не останавливаясь на истории вопроса, обратимся к опытам по изучению гидравлических сопротивлений в шероховатых трубах, произведенным А.Никурадзе еще в 1932 году и не утратившим своего значения до настоящего времени. Указанные опыты были поставлены весьма тщательно и проводились в трубах с искусственной однородной шероховатостью, которая создавалась накаливанием зерен песка определенного размера на внутреннюю поверхность труб. В трубах с полученной таким образом определенной шероховатостью при разных расходах измерялась потеря напора, и по формуле высчитывался коэффициент l, значения которого наносились на график в функции числа Рейнольдса.

 

 

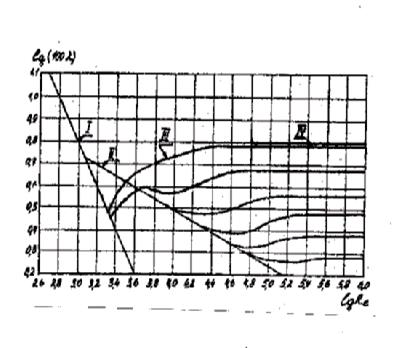Рисунок 4. График Никурадзе.

 

Результаты опытов Никурадзе представлены графически на рисунке 4.

 

 

На этом графике по горизонтальной оси отложены величины 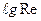, а по вертикальной оси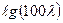 /100l/. Кривые построены по данным опытов с трубами различной относительной шероховатости от 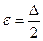= 0,00197 (самая нижняя кривая) 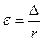= 0,0666 до 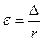=0,0666 (самая верхняя кривая).

Из данных полученных Никурадзе, следует, что зависимость 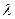от числа Рейнольдса может быть разделена на несколько зон.

1 зона. Это зона ламинарного режима в гидравлически гладких трубах, когда 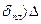. Коэффициенты гидравлического сопротивления этой зоны группируются вдоль прямой Пуазейля и подсчитываются по формуле:

 

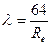; т.е.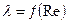

не зависит от шероховатости труб.

II зона. Это зона турбулентного режима движения жидкости в гидравлически гладких трубах. В этой зоне потери энергии не зависят от шероховатости стенок труб, а λ зависит только от числа Рейнольдса, т.е.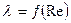

Коэффициент гидравлического сопротивления этой зоны на графике группируется вдоль прямой Блазиуса и определяется по формулам

 

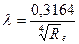- для чисел при Re<10⁵ /формула Блазиуса/

 

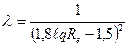- для любых /Re/формула Канакова/

 

Полевые трубопроводы, применяемые в трубопроводных войсках Российской Армии, считаются гидравлически гладкими. При определении коэффициента гидравлического сопротивления 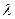для них применяются следующие формулы:

 

для трубопроводов типа ПМТ

 

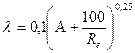
где: А = 0,00014 - для крашеных и алюминиевых труб;

А = 0,00045 - для оцинкованных и черных труб;

 

для трубопроводов типа ПМТП

 

 

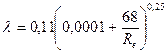
для трубопроводов типа ПМТБ

 

 

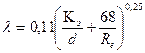
где: К_э - эквивалентная шероховатость.

Технические трубы считаются гидравлически гладкими до значений

 

R_е=27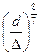

 

Конец второй зоны и переход к третьей зоне можно определить по формуле - относительная шероховатость

 

,

где 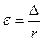– относительная шероховатость

 

Если вычисленное число 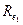< 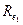- труба гидравлически гладкая, а если 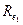> 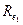- - труба шероховатая.

По этой формуле определяют переходную зону от гладких труб к шероховатым.

III зона, Это зона турбулентного режима движения жидкости в шероховатых трубах. Коэффициенты гидравлического сопротивления в этой зоне на графике группируются на изгибах прямых до выхода их на горизонтальные прямые. В этой зоне l зависит как от числа R_е, так и от 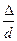- относительной шероховатости. Наиболее удобно вычислять 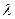для этой зоны по формуле Альтшуля:

 

 

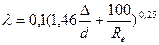
Верхняя граница третьей зоны ориентировочно определяется выражением:

R_е=500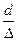

IV зона. - зона квадратичного сопротивления отвечает такому турбулентному движению жидкости во вполне шероховатых трубах, в которых коэффициент трения l зависит только от относительной шероховатости 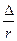. Потеря напора для этой зоны пропорциональна квадрату скорости.

В квадратной зоне турбулентного движения коэффициент гидравлического сопротивления l для труб одинаковой относительной шероховатости имеет одинаковое значение.

По опытам Никурадзе коэффициент гидравлического сопротивления для квадратичной зоны турбулентного движения во вполне шероховатых трубах определяется по формуле:

 

,

 

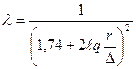где r-радиус трубы.

 

 

Вывод по третьему вопросу

 

Одной из сложных проблем при гидравлических расчётах является определение коэффициента гидравлического сопротивления. Изученный график Никурадзе позволяет решить эту проблему.

 

Гидравлический уклон

 

Частично при решении гидравлических задач пользуются понятием Гидравлический уклон.

Гидравлическим уклоном называется потеря напора на трение на единицу длины трубопровода и обозначается буквой

Исходя из определения гидравлический уклон, можно выразить формулой:

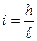
где h - потеря напора на трение на длине 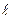трубопровода

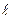- длина трубопровода

Если выразить потерю напора на трение по длине трубопровода по формуле Дарси-Вейсбаха, тогда гидравлический уклон можно обозначить:

 

 

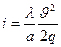
Гидравлический уклон представляет собой гипотенузу прямоугольного треугольника, у которой вертикальный катет в определенном масштабе выражает общие потери по длине трубопровода, а горизонтальный катет в определенном масштабе выражает длину трубопровода (рис.)

Согласно определению гидравлического уклона можно записать:

 

,

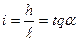тогда

 

 

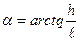
h

 

Рисунок 4.

 

Зная угол α, можно провести линию гидравлического уклона.