Классная работа
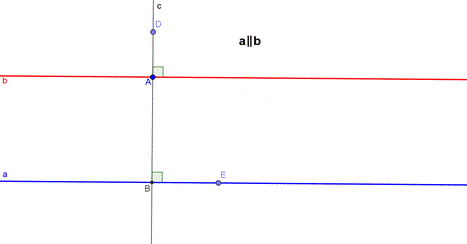
1. Задача ( чертёж перестраиваете в тетрадь. Углы обозначить цифрами. Дано можно не писать)
Доказать параллельность прямых и вычислить все углы, полученные при пересечении двух прямых секущей.
Тема урока: Аксиома параллельных прямых
(тему урока записываем в тетрадь).
Изучение нового материала
Аксиома – это утверждение, которое принимается без доказательства. (Определение записываем в тетрадь).
(Примеры аксиом выписать из презентации, слайд 3).
- Там, где с морем сливается Нил,
В древнем жарком краю пирамид,
математик греческий жил –
много знающий мудрый Эвклид.
Геометрию он изучал.
Геометрии он обучал.
Написал он великий труд.
Эту книгу «Начала» зовут.
(Стих – е переписывать в тетрадь не нужно).
- Эвклид - древнегреческий ученый. Написал знаменитое сочинение «Начала», являющееся и в наше время важным трудом т.к. ряд его высказываний, изложенных в «Началах» и сейчас используют в курсах геометрии, а сама геометрия, изложенная в «Началах» называется Евклидовой геометрией.
(Переписываем текст из презентации, слайды 4, 5, 6)
(Читать слайды из презентации 7, 8)
(Переписать из презентации слайды 9,10).
Итак, еще раз вернемся к нашему ученому Н.И. Лобачевскому
Оказывается, кроме геометрии, которую изучают в школе, есть и другие геометрии, в которых нет параллельных прямых. Посмотрите на глобус, вот вам пример геометрии кривого пространства: меридианы пересекаются в двух точках, в северном и южном полюсах.
Прочитайте об этом стихотворение.
- «Да! Конечно, да! Доказывать бесцельно!
Параллельные пойдут не параллельно
там, где звездный мир раскинулся без края!
Аксиома параллелей там – другая!
Параллельно геометрии Эвклида
есть еще одна – совсем другого вида!»
Смотрел он долго в зимнее окно.
Горели звезды в небе над Казанью –
Вселенная была с ним заодно.
Открылся чистый купол мирозданья,
и звезды в вышине огнем горели,
твердя: не параллельны параллели!»
Задача (Чертёж в тетрадь, всё, что жирным шрифтом записываем в тетрадь): Можно ли через точку, не лежащую на прямой, провести прямую, параллельную данной.
Возникает вопрос: а сколько таких прямых можно провести?
И так, Аксиома параллельных прямых или пятый постулат Евклида:
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
А как это доказать?
Может существует еще одна прямая b/, проходящая через точку М и параллельная прямой а?
Оказывается, доказать это невозможно, хотя ученые на протяжении многих веков пытались это сделать. Называли эту проблему проблемой пятого постулата, потому что в геометрии Евклида это утверждение называлось пятым постулатом.
И стояла геометрия Евклида,
Как египетское чудо - пирамида.
Строже выдумать строенья невозможно,
Лишь одна в ней глыба была ненадежна.
Аксиома называлась «Параллели»,
Разгадать ее загадку не сумели…
И лишь в прошлом веке, во многом благодаря великому русскому математику Н.И. Лобачевскому, было доказано, что пятый постулат не может быть выведен из остальных аксиом. Поэтому утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, принимается в качестве аксиомы.
(Переписать в тетрадь 12 слайд)
До следующих встреч!
