Пример 2.3.1. Пусть А – подгруппа из нормализатора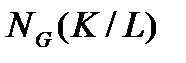 
секции 
группы G. Зададим действие А на сопряжением: 
для любого 
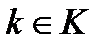и для любого 
. Тогда А – группа операторов группы , причем множество всех тождественных операторов из А совпадает с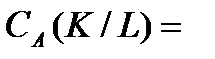 
. В частности, если 
, то G является группой операторов своей нормальной секции , причем G действует тождественно на тогда и только тогда, когда центральна в G, т.е. 
.
В дальнейшем при рассмотрении действия подгрупп из G на секциях группы G без указания способа задания действия, будем иметь в виду действие, описанное в примере 2.2.1.
Определение 2.3.13. Пусть G и Н являются 
- операторными группами. Группа G называется А-изоморфной группе Н, если существует изоморфное отображение 
группы G на Н такое, что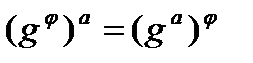 
для любого 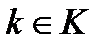и для любого .
Лемма 2.3.2. Пусть А-операторная группа G обладает А-композиционным (конечным) рядом длины 
и 
имеет нормальные А-допустимые подгруппы 
Тогда каждый А-композиционный фактор группы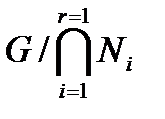 
А-изоморфен некоторому А-композиционному фактору хотя бы одной из групп 
и 
.
Доказательство. При 
утверждение леммы верно. Допустим, что утверждение верно для 
нормальной в G А -допустимой подгруппы. Пусть 
. Тогда подгруппа 
нормальна в G и А -допустима. Далее, 
и 
А -допустима и нормальна в 
. Так как группа 
А -изоморфна группе 
то каждый А -композиционный фактор группы 
А -изоморфен А -композиционно-
му фактору либо группы 
и значит по предложению индукции некоторой группы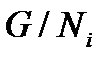 
, 
, либо группы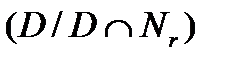 
А -изоморфной группе 
и значит группы , причем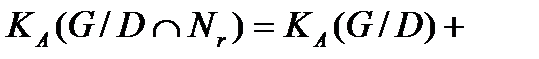 
Лемма доказана.
Следствие 2.3.2. Пусть группа G обладает главным (конечным) рядом и 
– нормальные подгруппы группы G. Тогда каждый главный фактор группы 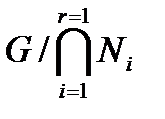G-изоморфен главному фактору хотя бы одной из групп 
и 
.
Доказательство. Полагаем по лемме 2.3.2 
. Тогда А -композиционный фактор групп G, 
является главным фактором этих групп. Следствие доказано.
Лемма 2.3.3. Пусть 
и 
– нормальные секции группы G. Если и G-изоморфны, то 
Доказательство. Пусть 
является G -изоморфизмом и . Тогда 
для любого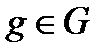 
и для любого 
. Следовательно, 
. Пусть 
. Тогда 
для любого . Поэтому 
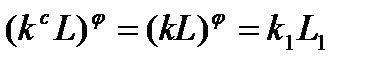, и значит, 
для любого 
. Так как 
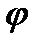является отображением на , то когда 
пробегает группу , то 
пробегает группу . Следовательно, для любого и 
. Поэтому 
. Рассматривая отображение 
, в силу симметрии, аналогично получим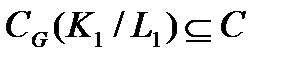 
. Следовательно, 
.
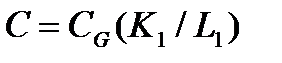Лемма 2.3.4. а) Если – главный фактор конечной группы G и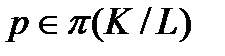 
, то 
не содержит неединичных нормальных р-подгрупп, причем, 
,где 
– наибольшая нормальная р-нильпотентная подгруппа группы G;
б) если G – конечная А-операторная группа и 
– А-композиционный р-фактор группы G, то 
не имеет неединичных нормальных р-подгрупп.
Доказательство. а) Пусть 
и 
. Тогда по следствию 2.3.1 
и 
Пусть является неабелевой 
-группой. Так как является минимальной нормальной подгруппой группы 
, то является прямым произведением изоморфных неабелевых простых -групп. Тогда 
, и значит, 
. Далее 
G -изоморфен группе 
. Тогда в группе 
подгруппа 
является неабелевой минимальной нормальной -группой. По лемме 2.3.5 
. Следовательно, имеет единичный централизатор в группе . Отсюда следует, что 
не имеет неединичных нормальных 
-подгрупп и 
-подгрупп. Поэтому 
, и значит, 
.
Пусть теперь 
абелева -группа. Так как 
главный фактор группы G, то является элементарной абелевой -группой. По следствию 2.3.1 в) группа изоморфна некоторой подгруппе 
из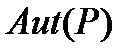 
. Так как является главным фактором группы G, то не существует -допустимой подгруппы 
в 
такой, что 
, т.е. действует на неприводимо. Тогда в полупрямом произведении 
А подгруппа 
является минимальной нормальной подгруппой. Допустим, что 
. Тогда 
нормальная -подгруппой группы 
. Так как 
нормальна в 
, то 
. Так как 
нормальна в и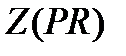 
характеристична в 
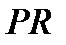, то 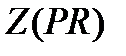нормальна в . Тогда 
нормальна в как пересечение нормальных подгрупп из . Так как 
минимальная нормальная подгруппа в и 
, то 
. Следовательно, 
. Так как 
и 
централизует , то 
. Получили противоречие. Значит, 
Если 
-подгруппа из 
, то 
характеристична в 
, и значит, 
нормальна в G. Рассмотрим группу 
. Тогда 
и являются нормальными подгруппами группы , причем 
является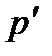 
-подгруппой, а элементарной абелевой -группой. Тогда и поэлементно перестановочны. Значит, 
. Следовательно, 
. Поэтому 
, и значит, 
. Утверждение а) доказано.
б) Так как 
-композиционный -фактор группы G, то в М не существует -допустимой нормальной подгруппы 
такой, что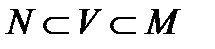 
. Тогда в полупрямом произведении 
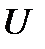подгруппа 
является минимальной нормальной подгруппой и значит 
A=X является элементарной абелевой -группой. По пункту а) 
не имеет неединичных нормальных -подгрупп. Так как 
, то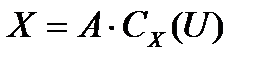 
. Тогда 
, и значит, 
не имеет неединичных нормальных -подгрупп. Лемма доказана.
Заключение
В реферате выполнены следующие задачи:
§ Рассмотрены основные определения теории групп (определение группы, подгруппы, нормальной подгруппы, правого и левого смежного классов, нормализатора, централизатора подмножества в группе и другие).
§ Проведено исследование основных понятий, связанных с операторными группами.
§ Изучены простейшие свойства нормализаторов и централизаторов секций конечной группы.
§ Изучены основные свойства операторных групп.
Список литературы
1. Ведерников В.А. Элементы теории классов групп. – Смоленск, 1988.
2. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп. - М.: Наука, 1982.
3. Кострикин А. И. Введение в алгебру. Часть 1. Основы алгебры. - М.: Физико-математическая литература, 2000.
4. Кострикин А.И. Введение в алгебру. Часть 2. Линейная алгебра. - М.: Физико-математическая литература, 2000.
5. Кострикин А.И. Введение в алгебру. Часть 3. Основные структуры алгебры. - М.: Физико-математическая литература, 2000.
6. Кострикин А.И. Сборник задач по алгебре. - М.: Физико-математическая литература, 2001.
7. Курош А.Г. Теория групп. – М.: Физико-математическая литература, 2011.
8. Монахов В.С. Введение в теорию конечных групп и их классов: учебное пособие. – Мн.: Вышэйшая школа, 2006.
9. Скиба А.Н. Алгебра формаций. – Мн.: Беларуская навука, 1997.
10. Шеметков Л.А., Скиба А.Н. Формации алгебраических систем. – М.: Наука, 1989.
11. Шеметков. Л.А. Формации конечных групп. – М.: Наука, 1978.
