Описание лабораторной установки. Изучение закономерностей процесса осаждения твердых частиц в жидких и газообразных средах, со­поставление результатов исследований с критериаль­ными

ИССЛЕДОВАНИЕ ПРОЦЕССА СВОБОДНОГО ОСАЖДЕНИЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ

Цель работы

Изучение закономерностей процесса осаждения твердых частиц в жидких и газообразных средах, со­поставление результатов исследований с критериаль­ными уравнениями процесса осаждения, решение ос­новных задач при осаждении частиц.

Содержание работы

1. Ознакомиться с гидродинамикой движения твердых тел в жидкости под действием сил тяжести. Изучить следующие вопросы: условие равновесия сил, действующих на частицу, режимы движения тел в жид­кости, силы сопротивления движению тел, скорость свободного осаждения и формулы для ее определе­ния при различных режимах движения тел в жид­кости.

2. Исследовать процесс осаждения твердой части­цы с известной плотностью и диаметром в трех жид­костях с различной вязкостью. Экспериментально оп­ределить коэффициент удельной поверхности частицы и коэффициент формы и шероховатости поверхности частиц.

3. Решить прямую задачу процесса осаждения ше­роховатой несферической твердой частицы в жидко­сти под действием сил тяжести и рассчитать значе­ния скоростей осаждения твердой частицы в трех жидкостях с различной вязкостью.

4. Выполнить графическое сопоставление экспери­ментальных и расчетных значений скорости осаж­дения.

5. Рассмотреть решение обратной задачи процесса осаждения шероховатой несферической твердой частицы в жидкости под действием сил тяжести. Определить диаметр шероховатой несферической твердой частицы по скорости осаждения ее в трех жидкостях различной вязкости.

Теоретическая часть

3.1. Основные понятия и термины

В работе используются следующие термины и ос­новные понятия: свободное осаждение, скорость осаж­дения, сопротивление движению частиц в жидкостях, режимы движения твердых частиц в жидкостях, ко­эффициент удельной поверхности частиц, числа подо­бия Архимеда, Рейнольдса, Лященко. С этими тер­минами следует ознакомиться в (1, стр. 98—104).

3.2. Основные положения

3.2.1. Свободное гравитационное осаждение частицы в жидкости

В химической технологии широко распространены процессы разделения гетерогенных систем не отдель­ные фазы путем осаждения частиц дисперсной фазы в дисперсионной среде под действием различных мас­совых внешних сил. Так, для выделения твердых ча­стиц (например, кристаллов) из жидких или газообразных сред широко применяются отстойники, осно­ванные на осаждении частиц под действием силы тяжести.

В данной работе рассматривается свободное гра­витационное осаждение частиц в жидкости, при ко­тором процесс осаждения происходит под действием силы тяжести, и осаждающиеся частицы практически не оказывают влияния на движение друг друга.

При движении частицы в жидкости возникает сопротивление, величина которого зависит главным об­разом от режима движения, формы и поверхности движущейся частицы.

Наблюдаются два принципиально различных ре­жима движения частицы в жидкости: ламинарный и турбулентный. Ламинарный режим движения имеет место при малых размерах частиц и высокой вязко­сти среды, что обусловливает небольшие скорости

 

а) б)

Рис. 8.1. Движение твердо­го тела в жидкости:

а — ламинарный поток; б — турбулентный поток

 

движения частицы. В этом случае частица плавно об­текается потоком (см. рис. 8.1 а). Величина сопротив­ления определяется в основном лишь силами трения и давления вследствие сил вязкости.

Турбулентный режим движения частицы в жид­кости наблюдается при больших размерах частиц и малой вязкости среды, то есть при высоких скоро­стях движения частиц, когда все большую роль начи­нают играть силы инерции. Под действием этих сил происходит отрыв жидкости от поверхности частицы в кормовой части, что приводит к образованию бес­порядочных местных завихрений за движущейся ча­стицей (см. рис. 8.1б).

Сопротивление движению в данном случае, как и при движении жидкости по трубам, будет опреде­ляться в основном лишь силами инерции, а влиянием вязкостных сил можно пренебречь.

Переход от ламинарного к турбулентному движе­нию жидкости характеризуется критическими значе­ниями чисел Рейнольдса Re_кр1 и Архимеда Аr_кр1

где V_oc — скорость осаждения частицы, м/с;

— кинематическая вязкость среды, м² /c;

μ — динамическая вязкость среды. Па ^. с;

d — эквивалентный диаметр частицы, равный

где G_ч — вес частицы, Н;

— плотность материала частицы, кг/м³;

g — ускорение силы тяжести, м/с².

Число Архимеда

где — плотность материала среды, кг/м³.

При значениях Re_кр1 <2 и Аг_кр1 <36 движение ча­стицы в жидкости является ламинарным, при Re_кр1>500 и Аr_кр1 >83000— турбулентным, а при Re=2÷500 и Аг=36÷83000 имеет место переходная неустойчивая область.

3.2.2. Сила сопротивления среды

При движении частицы в жидкости на ее поверхность, в результате взаимодействия со средой, дейст­вуют нормальные и касательные напряжения, обу­словливающие силы гидродинамического давления и силы трения.

Векторная сумма действующих на поверхность частицы сил равна силе сопротивления среды, кото­рая имеет направление, противоположное вектору скорости движения частицы. Сила сопротивления сре­ды определяется по закону сопротивления Ньютона

где f — площадь «миделевого сечения», то есть се­чение тела плоскостью, пер

перпендикулярной скорости движения тела, м²;

ζ — коэффициент сопротивления среды, ζ=f (Re).

В области ламинарного режима движения частиц действует закон сопротивления Стокса

в турбулентной области—закон сопротивления Нью­тона

При ламинарном режиме сила сопротивления про­порциональна скорости в первой степени (закон Стокса)

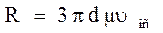
при турбулентном режиме сила сопротивления про­порциональна скорости во второй степени (закон Ньютона)

(8.8)

При любом режиме движения сила сопротивления может быть найдена по уравнению

3.2.3. Понятие о скорости осаждения

При падении частицы в жидкости под действием собственного веса в начальный момент времени дви­жение ее происходит с изменяющейся скоростью. Однако с увеличением скорости, согласно (8.4), растет сопротивление движению частицы и соответственно уменьшается ее ускорение. Через короткий промежу­ток времени наступает динамическое равновесие. При этом сила кажущегося веса частицы в жидкости, рав­ного разности между силой действительного веса и силой Архимеда, под действием которой она дви­жется, становится равной силе сопротивления среды. Ускорение движения практически исчезает, и части­ца начинает двигаться равномерно, с постоянной ско­ростью, направленной вниз (скорость осаждения), ес­ли ρ_ч>ρ_с, или вверх (скорость всплывания), если ρ_ч<ρ_с.

Таким образом, под скоростью осаждения пони­мают такую постоянную скорость, которую развивает частица, двигаясь вниз в сопротивляющейся среде под действием силы тяжести.

Условие динамического равновесия сил, действующих на частицу (см. рис. 8.2), то есть условие равномерного движения ее в жидкости, записывается в виде

 

Рис. 8.2. Схема сил, действующих на частицу

где подъемная Архимедова сила равна

а вес частицы G, определяется согласно (8.2). С учётом (8.2) и (8.11) условие (8.10) принимает вид

Скорость осаждения при ламинарном режиме движе­ния (закон Стокса) определится из равенства выра­жений (8.12) и (8.7)

при турбулентном режиме движения (закон Ньюто­на) находится из равенства выражений (8.12) и (8.8)

К недостатку формул (8.13) и (8.14) следует от­нести то, что пользоваться ими можно лишь в том случае, если заранее известен режим движения ча­стицы. В противном случае удобнее пользоваться кри­териальными зависимостями. Существует единое кри­териальное уравнение, справедливое для всех режи­мов осаждения (уравнение Тодоса),

и графические зависимости Re_oс=f (Ar) и Ly=f (Ar), экспериментально определенные для частиц различной формы и приведенные на рис. 8.3, где число Ля-щенко записывается в виде

3.2.4. Прямая задача процесса осаждения

Различают две задачи процесса осаждения под действием силы тяжести: прямую и обратную.

Под прямой задачей процесса осаждения понима­ют определение скорости осаждения при известном диаметре частицы.

Прямая задача осаждения частиц, близких к сфе­рическим, решается с помощью уравнения Тодоса (8.15) или графической зависимости Re_oc=f(Ar), изображенной на рис. 8.3

а также с помощью графической зависимости (рис. 8.З) Ly=f (Ar)

Прямая задача осаждения частиц, отличающихся от гладких сферических, решается аналогично по фор­муле

где φ_п — коэффициент удельной поверхности части­цы, учитывающей отношение поверхности частицы к поверхности сферы равного объема;

φ_ф— коэффициент формы и шероховатости ча­стиц.

Рис. 8.3. Зависимость чисел Re и Ly от числа Аг для осаждения одиночной частицы в неподвижной среде:

1 и 6 — шарообразные частицы; 2— округлые; 3— угловатые; 4— продолговатые; 5— пластинчатые

Значение коэффициентов φ_п и φ_ф для различных форм частиц приведено в таблице 8.1.

3.2.5. Обратная задача процесса осаждения

Обратная задача процесса осаждения состоит в оп­ределении диаметра частицы при известной скорости осаждения. Она решается с помощью графических зависимостей Аг=f (Ly). показанных на рис. 8.3.

Таблица 8.1

Значения коэффициентов φ_п и φ_ф

Форма частиц	φп	φф
Гладкие сферические Округлые Угловатые Продолговатые Пластинчатые	1,18 1,33 1,34 1,53	1,27 1,45 1,96 3,42

 

Обратную задачу осаждения можно решать также с помощью формулы

Описание лабораторной установки

Установка (рис. 8.4) для экспериментального оп­ределения скорости осаждения твердых частиц в раз­личных жидких средах состоит из трех стеклянных цилиндров 1, укрепленных вертикально на подстав­ке 2. На дне каждого цилиндра установлены сетчатые ловушки 3 с державкой 4. На поверхности цилиндров нанесены две метки: одна метка «а» несколько ниже уровня жидкости, другая метка «б» несколько выше дна цилиндрического сосуда. Расстояние от поверхно­сти жидкости до уровня метки «а» необходимо для достижения частицей постоянной скорости осажде­ния. Цилиндры заполнены различными жидкостями:один—водой, второй—машинным маслом, третий— глицерином. К установке прилагается набор твердых частиц различного диаметра и из различных матери­алов, пинцеты, ветошь, секундомер и микрометр.