У логіці висловлювань були введені дві нормальні форми: кон’юнктивна і диз’юнктивна. В аксіоматичній системі логік вводиться третя нормальна форма, яку називають випередженою нормальною формою.
Означення 4.2.1. Формула Ф у логіці предикатів знаходиться у випередженій нормальній формі (ВНФ) тоді і тільки тоді, коли вона може бути зображена у вигляді ( )… (
)… (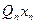 ) (А), де (
) (А), де ( ) є або (
) є або ( х), або (
х), або ( х) і всі
х) і всі  різні для різних і = 1, …, п, а А – формула, що не містить квантора. Приставку (
різні для різних і = 1, …, п, а А – формула, що не містить квантора. Приставку ( ) називають префіксом, а А – матрицею формули Ф. Якщо формула А залежить від вільної змінної х, то це записується як А (х), якщо ні, то – А.
) називають префіксом, а А – матрицею формули Ф. Якщо формула А залежить від вільної змінної х, то це записується як А (х), якщо ні, то – А.
Теорема 4.2.1. Для будь-яких формул F, G, H теорії числення першого порядку справедливі такі еквівалентності:
а) 
 х F(x)
х F(x) 
 х (
х ( F (x));
F (x));
б) 
 х F(x)
х F(x) 
 х (
х ( F(x));
F(x));
в)  х F(x)
х F(x)  G
G 
 х (F(x)
х (F(x)  G);
G);
 х F(x)
х F(x)  G
G 
 х (F(x)
х (F(x)  G);
G);
г)  х F(x)
х F(x)  G
G 
 х (F(x)
х (F(x)  G);
G);
 х F(x)
х F(x)  G
G 
 х (F(x)
х (F(x)  G);
G);
д)  х F(x)
х F(x) 
 х Н (х)
х Н (х) 
 х (F(x)
х (F(x)  Н (х));
Н (х));
е)  х F(x)
х F(x) 
 х Н (х)
х Н (х) 
 х (F(x)
х (F(x)  Н (х));
Н (х));
є)  х F(x)
х F(x) 
 х Н (х)
х Н (х) 
 х
х  у (F(x)
у (F(x)  Н (у));
Н (у));
ж)  х F(x)
х F(x) 
 х Н (х)
х Н (х) 
 х
х  у (F(x)
у (F(x)  Н (у)).
Н (у)).
Доведення. Виконаємо доведення еквівалентності.
а) 
 х F(x)
х F(x) 
 х (
х ( F(x)). Нехай r – довільна інтер-претація на деякій області R. Якщо
F(x)). Нехай r – довільна інтер-претація на деякій області R. Якщо  (
( х F(x)) істинна в інтерпретації r, то
х F(x)) істинна в інтерпретації r, то  х F(x) хибна в r. Це означає, що існує такий елемент k(x)
х F(x) хибна в r. Це означає, що існує такий елемент k(x)  R, для якого F (k (x)) хибна, або те саме, що
R, для якого F (k (x)) хибна, або те саме, що  F (k (x)) істинна в r. Отже,
F (k (x)) істинна в r. Отже,  х (
х ( F(x)) істинна в r.
F(x)) істинна в r.
Якщо  (
( х F(x)) хибна в r, то
х F(x)) хибна в r, то  х F(x) істинна в r. Це означає, що F(x) виконується на всіх послідовностях із R або що
х F(x) істинна в r. Це означає, що F(x) виконується на всіх послідовностях із R або що  F(x) не виконується на жодній такій послідовності з R. Отже,
F(x) не виконується на жодній такій послідовності з R. Отже,  х (
х ( F(x)) хибна в r. Таким чином,
F(x)) хибна в r. Таким чином,
 (
( х F(x))
х F(x)) 
 х (
х ( F(x)).
F(x)).
Доведення еквівалентності б) аналогічне доведенню еквівалентності а).
Доведемо еквівалентність в)  х F(x)
х F(x)  G
G 
Û  х (F(x)
х (F(x)  G). Нехай маємо
G). Нехай маємо  хF(x)
хF(x)  G
G 
 (
( хF(x))→ →G
хF(x))→ →G 
 х (
х ( F(x)) → G.
F(x)) → G.
Отже,
1)  х (
х ( F(x)) → G – гіпотеза;
F(x)) → G – гіпотеза;
2)  F(x) →
F(x) →  х (
х ( F(x)) – правило 7;
F(x)) – правило 7;
3)  F(x) → G – транзитивність із 1) і 2);
F(x) → G – транзитивність із 1) і 2);
4) 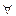 x (
x ( F(x) → G)
F(x) → G) 
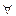 x (F(x)
x (F(x)  G) – загальнозначність із 3).
G) – загальнозначність із 3).
І навпаки:
1) 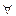 x (F(x)
x (F(x)  G)
G) 
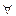 x (
x ( F(x) → G) – гіпотеза;
F(x) → G) – гіпотеза;
2)  F(x) → G – правило 6 із 1;
F(x) → G – правило 6 із 1;
3) ( F(x) → G) → (
F(x) → G) → ( G → F(x)) ‒ тавтологія;
G → F(x)) ‒ тавтологія;
4)  G → F(x) – МР із 2) і 3);
G → F(x) – МР із 2) і 3);
5) 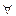 x (
x ( G → F(x)) – узагальнення із 4;
G → F(x)) – узагальнення із 4;
6)  х (
х ( G → F(x)) → (
G → F(x)) → ( G →
G →  х F(x)) – схема аксіом АП5;
х F(x)) – схема аксіом АП5;
7)  G →
G → 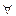 x F(x) – МР із 5 і 6;
x F(x) – МР із 5 і 6;
8) ( G →
G → 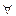 xF(x)) → (
xF(x)) → (
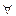 x F(x) → G) – тавтологія;
x F(x) → G) – тавтологія;
9) 
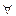 x F(x) → G
x F(x) → G 
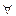 x F(x)
x F(x)  G – МР із 7) і 8).
G – МР із 7) і 8).
Доведемо спочатку першу еквівалентність г).
1)  х F(x)
х F(x)  G
G 
 х (
х ( F(x)) → G – гіпотеза;
F(x)) → G – гіпотеза;
2) ( F(x)) → G – правило 6;
F(x)) → G – правило 6;
3) ( F(x)) → G) →
F(x)) → G) →  х (
х ( F(x) → G) – правило 7;
F(x) → G) – правило 7;
4)  х (
х ( F(x)
F(x)  G)
G) 
 х (F(x)
х (F(x)  G) – МР із 2) і 3).
G) – МР із 2) і 3).
І навпаки:
1)  х (
х ( F(x) → G) – гіпотеза;
F(x) → G) – гіпотеза;
2)  х (
х ( F(x) → G) → (
F(x) → G) → ( F(x) → G) – правило 7;
F(x) → G) – правило 7;
3)  F(x) → G – МР із 1) і 2);
F(x) → G – МР із 1) і 2);
4) 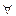 x (
x ( F(x)) →
F(x)) →  F(x) – правило 6;
F(x) – правило 6;
5) 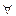 x (
x ( F(x)) → G
F(x)) → G 

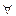 x (
x ( F(x))
F(x))  G
G 
 х (F(x))
х (F(x))  G – транзитивність із 3) і 4).
G – транзитивність із 3) і 4).
Доведення інших еквівалентностей із в) і г) тепер легко випливає із законів де Моргана.
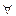 x F(x)
x F(x)  G
G 
 (
(
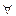 x F(x)
x F(x) 
 G)
G) 
Û ((  х
х  F(x))
F(x)) 
 G
G 
 (
(  х (
х ( F(x)
F(x) 
 G)
G) 
Û  (
(  х
х  (F(x)
(F(x)  G)
G) 
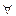 x (F(x))
x (F(x))  G).
G).
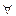 x F(x)
x F(x)  G
G 
 (
(
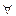 x F(x)
x F(x) 
 G)
G) 
Û(  х (
х ( F(x))
F(x)) 
 G)
G) 
 (
(  х (
х ( F(x)
F(x) 
 G)
G)  Û
Û  (
(  х
х  (F(x)
(F(x)  G)
G) 
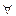 x (F(x)
x (F(x)  G).
G).
Аналогічно доводяться й інші еквівалентності із г).
Доведення решти еквівалентностей пропонуються як вправи.
Теорема доведена.
Із теореми 4.2.1 випливає такий метод побудови ВНФ. Для зведення формули Ф до випередженої нормальної форми використовують такі дії:
а) вилучення логічних зв’язок “ →” і “  ”:
”:
А  В = (А → В)
В = (А → В)  (В → А); А → В =
(В → А); А → В =  А
А  В;
В;
б) вилучення і перенесення знака “  ” всередину формул:
” всередину формул:
 (
( x F(x)) =
x F(x)) =  х (
х ( F(x));
F(x));  (
(  х F(x)) =
х F(x)) =
= 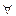 x (
x ( F(x));
F(x)); 
 F = F;
F = F;
в) перенесення кванторів:
Q x Р(х)  G = Q x (F(x)
G = Q x (F(x)  G);
G);
Q x Р(х)  G = Q x (F(x)
G = Q x (F(x)  G);
G);
 х F(x)
х F(x) 
 х Н (х) =
х Н (х) =  х (F(x)
х (F(x)  Н (х));
Н (х));
 х F(x)
х F(x) 
 х Н (х) =
х Н (х) =  х (F(x)
х (F(x)  Н (х));
Н (х));
Q1 х F(x) 
 х Н (х) =
х Н (х) =  х
х  у (F(x)
у (F(x)  Н (у));
Н (у));
Q1 х F(x) 
 х Н (х) =
х Н (х) =  х
х  у (F(x)
у (F(x)  Н (у)).
Н (у)).
Виходячи із методу побудови ВНФ, алгоритм отримання випередженої нормальної форми матиме такі кроки.
1. Вилучити логічні зв’язки еквіваленції “  ” та імплікації “ →” за допомогою правил а).
” та імплікації “ →” за допомогою правил а).
2. Перенести знак операції заперечення “  ” всередину формул, користуючись правилами:
” всередину формул, користуючись правилами:  (F
(F  G) =
G) =
 F
F 
 G;
G;  (F
(F  G) =
G) =  F
F 
 G, і правилами б).
G, і правилами б).
3. Виконати перейменування пов’язаних змінних, якщо є така необхідність.
4. Винести квантори на початок формули, використовуючи правила в).
Обґрунтуванням цього алгоритму є твердження, що безпосередньо випливає з теореми 4.2.1.
Теорема 4.2.2. Алгоритм випередженої нормальної форми перетворює будь-яку формулу А теорії числення предикатів першого порядку АП в таку формулу В, яка знаходиться у ВНФ, що ├ А  В у ПL.
В у ПL.
Приклад 4.2.1. Звести формулу  х F(x) →
х F(x) →  х Н (х) до ВНФ.
х Н (х) до ВНФ.
Розв’язання. Користуючись кроками 1, 2, 4 алгоритму, отримаємо
 х F(x) →
х F(x) →  х Н (х) =
х Н (х) =  (
( х F(x))
х F(x)) 
 х Н (х) =
х Н (х) =
=  х (
х ( F(x))
F(x)) 
 х Н (х) =
х Н (х) =  х (
х ( F(x)
F(x)  Н (х)).
Н (х)).
Приклад 4.2.2. Отримати ВНФ для формули
 х
х  у
у  z (Р (х, у)
z (Р (х, у)  Р(у, z)) →
Р(у, z)) →  z R(x, y, z).
z R(x, y, z).
Розв’язання. Користуючись кроками 1, 2, 3, 4 алгоритму, отримаємо
 х
х  у
у  z (Р (х, у)
z (Р (х, у)  Р (у, z)) →
Р (у, z)) →  z R(x, y, z) =
z R(x, y, z) =
=( z
z  y (
y (
 z (Р(х, у)
z (Р(х, у)  Р(у, z))
Р(у, z)) 
 z R(х, у, z) =
z R(х, у, z) =
=  x
x  y
y  z (
z ( Р(х, у)
Р(х, у) 
 Р(у, z))
Р(у, z)) 
 u R(х, у, и) =
u R(х, у, и) =
=  x
x  y
y  z
z  u (
u ( Р(х, у)
Р(х, у) 
 Р(у, z)
Р(у, z)  R(х, у, и)).
R(х, у, и)).
Оскільки матриця А формули Ф не містить кванторів, то її можна подати у кон’юнктивній нормальній формі (КНФ). Формула Р знаходиться у кон’юнктивній нормальній формі, якщо вона має вигляд Р =  …
… 
 ,
,
де  =
= 


 …
… 
 , і кожне
, і кожне  ‒ це атомарна формула або її заперечення.
‒ це атомарна формула або її заперечення.






