Свойства линий магнитной индукции:
· непрерывны
· нигде не пересекаются
· Всегда замкнуты
· выходят из северного магнитного полюса N и входят в южный магнитный полюс S
· густота линий пропорциональна модулю вектора В
Магнитные линии можно «увидеть» по расположению стальных опилок или магнитных стрелок вокруг проводников с током.
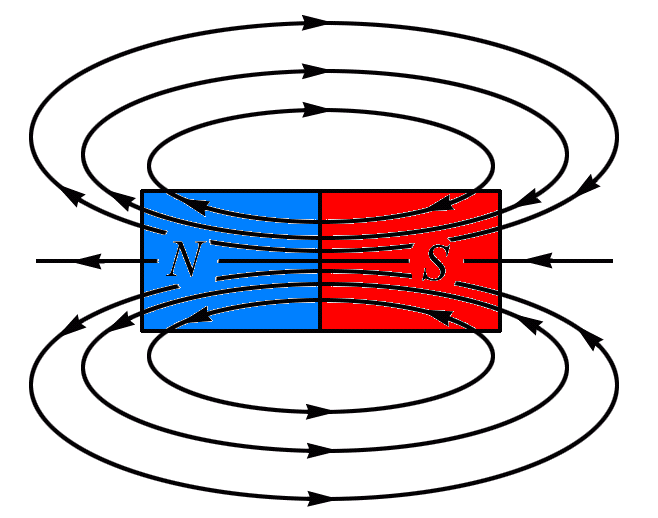
ПОСТОЯННЫЙ МАГНИТ
КРУГОВОЙ ТОК СОЛЕНОИД
Направлениемагнитных силовых линий или линий вектора магнитной индукции определяется по правилу правого винта. Так если большой палец правой руки расположить по направлению тока в проводе, то четыре пальца правой руки обхватывающие проводник, покажут направление магнитных линий поля вокруг проводника.
Правило правого винта обладает свойством инверсии. Так если большой палец правой руки расположить по направлению тока в проводе, то четыре пальца правой руки обхватывающие проводник, покажут направление магнитных линий поля вокруг проводника.
Магнитное поле, в каждой точке которого вектор магнитной
индукции одинаков, называется однородным. Линии магнитной индукции однородного поля представляют собой параллельные прямые, расположенные на одинаковом расстоянии друг от друга. Чем гуще они располагаются, тем больше магнитная индукция.
Примером однородного магнитного поля является магнитное
поле внутри длинного соленоида — катушки с током.
Закон Гаусса для магнитного поля в дифференциальной и интегральной форме
Линии вектора 
не имеют ни начала, ни конца, т.к. они замкнуты.
Поток любого вектора через поверхность равен разности числа линий, начинающихся у поверхности, и числа линий, оканчивающихся внутри поверхности:
В соответствии с вышеизложенным, можно сделать заключение, что поток вектора через замкнутую поверхность должен быть равен нулю.
Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие:
Теорема Гаусса для вектора магнитной индукции в интегральной форме. Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
Этот результат является математическим выражением того, что в природе нет магнитных зарядов – источников магнитного поля, на которых начинались и заканчивались бы линии магнитной индукции.
Заменив поверхностный интеграл в объемным, получим:
Теорема Гаусса для вектора магнитной индукции в дифференциальной форме.Магнитное поле обладает тем свойством, что дивергенция его вектора 
всюду равна нулю:
Компьютерная модель магнитного поля Земли, подтверждающая его вихревой характер, изображена на рисунке.
Закон Био-Савара-Лапласа
Французы Био и Савар провели в 1820 году серию кропотливых и
разнообразных экспериментов по определению индукции магнитного
поля, созданного проводниками различной формы и конфигурации
с током. Био и Савар экспериментально определили, что магнитная индукция зависит от:
1) тока I, протекающего по проводнику,
2) формы и размеров проводника,
3) положения точки относительно проводника,
4) состояния окружающей среды (магнитной проницаемости).
Выявить закономерность, проанализировав весь этот
богатый массив эмпирической информации, удалось Лапласу.
Лаплáс Пьер-Симóн (1749–1827) – французский математик, физик и астроном; известен работами
в области небесной механики, дифференциальных уравнений, один из создателей теории
вероятностей. Именно Лаплас ввёл этот термин «Небесная механика».
Он пришёл к выводу, что определить магнитное поле, созданное
проводником произвольной формы с током, можно суммируя
индукцию магнитного поля d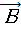 
от каждого отдельного «элемента
тока» Idl в произвольной точке пространства А, задаваемой радиус-
вектором 
.
Закон Био–Савара – Лапласа (БСЛ).
где μ 0 = 4 π∙ 10 -7 [Гн / м; Н/А2] – магнитная постоянная,μ- магнитная проницаемость μ= В в среде/В в вакууме
Модуль магнитной индукции от элемента тока
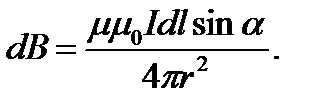
НАПРАВЛЕНИЕ ВЕКТОРА 
ОПРЕДЕЛЯЕТСЯ ПО ПРАВИЛУ ПРАВОГО ВИНТА ДЛЯ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
Для нахождения результирующего
магнитного поля созданного всем проводником следует, пользуясь
принципом суперпозиции полей, найти сумму векторов dВ
от всех элементов тока, на которые предварительно разбивается
проводник. Таким образом, принципиально может быть решён
вопрос для проводников произвольной формы.
Пример 1. Найти индукцию магнитного поля прямолинейного
проводника с током
“Разобьём” проводник на малые элементы и
определим индукцию магнитного поля в точке А для каждого из
них в соответствии с законом Био–Савара–Лапласа.
Направление векторов определим по «правилу буравчика».
Все векторы от произвольных элементарных участков имеют одинаковое направление ОТ НАС. Поэтому сложение векторов можно заменить сложением модулей.
Пусть точка, в которой определяется магнитное поле, находится на расстоянии b от провода. Из рисунка видно, что:
.
Подставив найденные значения r и d l в закон Био–Савара–Лапласа, получим:
Для проводника конечной длины угол α изменяется
от α1, до α2. Тогда
Для бесконечно длинного проводника α1=0, α2 = π, тогда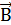 
или, что удобнее для расчетов,
Линии магнитной индукции прямого тока представляют собой систему концентрических окружностей, охватывающих ток.
.
