Построение линий влияния усилий в элементах ферм

 

 

Рис. 3. Построение л.в. усилий в элементах фермы

Передача нагрузки на ферму производится в узлах-шарнирах; следовательно, здесь мы имеем случай узловой передачи нагрузки.

Аналогично способам определения усилий в фермах при неподвижной нагрузке различаются следующие приемы построения линий влияния для ферм:

1) способ моментной точки,

2) способ проекций.

Способ моментной точки. Построим линию влияния усилия в стержне 7-9 фермы, изображенной на рис. 3, а. Проведем сечение 1-1, пересекающее три стержня.

Когда груз Р = 1 находится правее узла 8 (движение груза происходит по нижнему поясу фермы), удобнее рассматривать равновесие левой отсеченной части (рис. 3, б), так как в этом случае действует меньше сил, чем на правую. Применяя для определения усилия N_7-9 способ моментной точки, составим уравнение суммы моментов всех сил, действующих на левую часть фермы, относительно точки 6:

SМ₆ = R_A× 3d – N_7-9 h = 0,

откуда

N_7-9 = 3R_A d/ h.

Таким образом, при положении груза Р = 1 на правой части фермы усилие N_7-9 равно левой опорной реакции R_A, умноженной на постоянный коэффициент 3d/ h. Одновременно отмечаем, что 3R_A d численно равно изгибающему моменту М₆° в простой балке для сечения с абсциссой, равной абциссе моментной точки 6.

Линия влияния усилия N_7-9 (когда груз Р = 1 расположен правее представляет собой линию влияния опорной реакции R_A с ординатами, умноженными на 3d/h. Поэтому для ее построения отложим на оси отсчета вверх на левой опорной вертикали ординату, равную 3d/h, и соединим прямой ее вершину с нулевой точкой на правой опорной вертикали; в результате получим прямую а₁b (рис. 3, г).

На построенную таким образом прямую, называемую правой пр мой, сносим правые узлы фермы 5, 10, 12, 14 и 16. Заштриховываем линию влияния на участке между узлами 8 и 16.

При грузе Р = 1, расположенном левее узла б, усилие в стержне 7-9 может быть найдено из уравнения равновесия для правой части фермы (рис. 3, в):

S М₆ = — R_B. 5d + N_7-9 h = 0,

откуда

N_7-9 = 5 R_Bd/h,

т. е. усилие в стержне 7—9 равно правой опорной реакции R_В, увеличенной в 5d/h раз. Произведение 5R_Bd численно равно изгибающему моменту простой балки для сечения с абсциссой, равной абсциссе моментной точки 6.

Линия влияния N_7-9 для груза, расположенного левее узла 6, строится следующим образом: от оси отсчета вверх на правой опорной вертикали откладывается ордината, равная 5d/h, после чего ее вершина соединяется с нулевой точкой на левой опорной вертикали (прямая b₁а на рис. 3, г). Построенная таким образом прямая носит название левой прямой; на эту прямую сносятся левые узлы фермы 1, 2, 4 и 6. Заштриховываем линию влияния на участке между узлами 1 и 6.

Так как усилие N_7-9 определяется формулой

N_7-9 = М₆⁰/ h,

то его линия влияния может быть получена из линии влияния изгибающего момента простой балки (для сечения, соответствующего вертикали, проходящей через моментную точку в ферме) умножением всех ее ординат на коэффициент 1/h. Поэтому прямые ab₁ u a₁b_L (левая и правая), соединяющие вершины опорных ординат с нулевыми точками на противоположных опорах, пересекаются друг с другом под моментной точкой (в точке с). Передатси ная прямая, соответствующая движению груза Р = 1 между узлами 6 и 8 рассеченной панели, в данном случае совпадает с продолжением правой прямой линии влияния.

Рассмотренный пример позволяет сформулировать порядок построения линий влияния усилий для элементов балочной фермы на двух опорах способом моментной точки:

1) при построении правой прямой следует отложить от оси отсчета на левой опорной вертикали (вверх или вниз, в зависимости от знака) ординату a/h, где а — расстояние от моментной точки до левой опорной вертикали, h — плечо определяемого усилия относительно моментной точки;

2) вершину опорной ординаты соединить с нулевой точкой на правой опорной вертикали;

3) на построенную таким образом правую прямую снести правые узлы фермы;

4) найти на правой прямой точку пересечения ее с левой прямой, для чего моментную точку снести на правую прямую;

5) точку пересечения правой и левой прямых соединить с нулевой точ­кой на левой опорной вертикали;

6) на построенную таким образом левую прямую снести левые узлы фер­мы;

7) вершины узловых ординат рассеченной панели соединить передаточ­ной прямой.

Можно начинать построение линии влияния и с левой прямой.

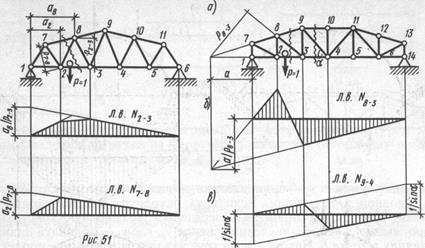
При параллельных поясах линии влияния усилий в раскосах и в стойках строятся как линии влияния поперечной силы для вертикального сечения, пересекающего раскос или стойку, с орди­натами, деленными на синус угла наклона раскоса (рис. 5, в), и со спрямлением на протяжении панели, по которой движется груз.

 

Рис. 5. Построение линий влияния усилий в элементах ферм

 

Нулевые стержни

 

Если в узле, соединяющем только два стержня, нагрузка отсутствует, то усилия в них равны нулю.

Если узел соединяет три стержня, из которых два направлены по одной прямой, то при отсутствии нагрузки в узле усилие в стержне 3 равно нулю (рис. 6), а если внешняя сила направлена вдоль этого стержня, то усилие в последнем равно внешней силе (рис. 7). При расчете статически определимой фермы полезно выявить таким способом «нулевые», т. е. неработающие, стержни и исключить их из дальнейшего расчета.

Например, в ферме, изображенной на рис. 8, неработающие стержни могут быть выявлены их последовательным исключением. Последовательность исключения обозначена на рисунке цифрами. Оставшиеся стержни, показанные жирными линиями, образуют значительно более простую ферму, чем первоначаль­но взятая.

 

 

10 11 4 2

 

Рис. 8 Рис. 6 Рис. 7