ЦЕНТР ТЯЖЕСТИ
Краткие сведения из теории
Центром тяжести тела называется точка приложения его силы тяжести.
Для нахождения положения центра тяжести используют следующие способы:
1 Метод симметрии. У однородного тела, имеющего плоскость, ось или центр симметрии, центр тяжести находится соответственно в плоскости, на оси или в центре симметрии.
2 Метод разбиения на части. Если тело имеет сложную форму, его разбивают на части, положения центров тяжести которых известны (формулы для расчета площадей и координат центров тяжести некоторых плоских фигур приведены в таблице 6.1). В таком случае положения центров тяжести тела определяют с использованием следующих выражений.
Координаты центра тяжести объемного тела постоянной плотности находятся по формулам
; 
; 
,
где 
– координаты центров тяжести элементарных частей,
– объем i -й части.
Если тело представляет собой однородную пластину постоянной толщины, то координаты ее центра тяжести
; 
, (6.1)
где 
– площадь i -го элемента.
Для стержневых конструкций, образованных стержнями одинаковой плотности и постоянного поперечного сечения, координаты центра тяжести определяют по формулам
; 
; 
,
где 
– длина элемента линии.
3 Метод отрицательных сил тяжести. При нахождении положения центра тяжести тела, имеющего вырезы, полости, отверстия и т. п., используют метод разбиения на части, причем считается, что полости (их площади, объемы) имеют отрицательный вес.
Таблица 6.1 – Площади и координаты центров тяжести плоских фигур
| Наименование | Расчетная схема | Площадь | Координаты центра тяжести |
| Круг | 
| 
| 
|
| Прямоугольник |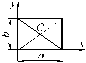 
| 
| 
|
| Треугольник | 
| 
|  ; 
|
| Круговой сектор |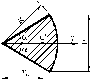 
| 
| 
|
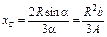
6.2 Пример решения задачи
Дано: схема плоской фигуры (рисунок 6.1). Размеры указаны в сантиметрах.
Определить координаты центра тяжести изображенной на рисунке пластины.
Решение.
1 Чтобы найти площадь заштрихованной фигуры, нужно от суммы площадей полукруга, сектора (четверти круга) и треугольника отнять площадь выреза (прямоугольника). Обозначим эти элементы цифрами, как это показано на рисунке 6.2, и укажем расположение их центров тяжести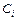 
.
2 Начало координат поместим в центре круга, а оси координат Ox и Oy направим горизонтально и вертикально.
3 Площадь полукруга и координаты его центра тяжести находим по формулам для кругового сектора из таблицы 6.1, учитывая, что α = π/2 рад:
4 Для нахождения площади и координат центра тяжести С 2 сектора 2 также воспользуемся таблицей 6.1. Размеры этого сектора определяются углом 
рад. Поэтому
.
|
). Медиана ОМ является также и высотой, поэтому
Тогда площадь и координаты центра тяжести треугольника 3:
|
6 Найдем площадь и координаты центра тяжести прямоугольника. Так как он является вырезом, его площадь берем со знаком “–”. Центр тяжести прямоугольника находится в точке пересечения его диагоналей. Следовательно,
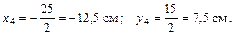
7 Координаты центра тяжести рассматриваемой пластины определяем по формулам (6.1):
7 По результатам расчета изображаем на рисунке точку С, являющуюся центром тяжести пластины.
Условие задания С-6
