Определение реакций связей рамной конструкции

РАВНОВЕСИЕ СИСТЕМЫ ТЕЛ

Некоторые сведения из теории

Системой тел называется конструкция, состоящая из нескольких твердых тел, взаимодействующих между собой через какие-нибудь связи, допускающие относительные перемещения этих тел (они могут соединяться шарнирами, гибкими нитями, опираться друг на друга и т. п.).

Силы, действующие на тела системы, делятся на внешние и внутренние.

Внешними называются силы, действующие на тела механической системы со стороны тел, не принадлежащих этой системе.

Внутренними называются силы взаимодействия между телами рассматриваемой системы.

При равновесии системы тел как каждое тело, так и вся система в целом находятся в равновесии. В связи с этим имеется два способа решения задач, связанных с исследованием равновесия системы тел:

1 Поскольку каждое тело системы находится в равновесии, то составляют уравнения равновесия каждого из тел (тогда уравнения равновесия системы в целом могут быть использованы для проверки правильности решения).

2 Сначала записывают уравнения равновесия системы в целом, а затем уравнения равновесия отдельных тел системы (в этом случае нет необходимости в составлении уравнений равновесия по крайней мере одного из тел системы, но они могут быть применены для проверки).

Замечания:

1 При составлении уравнений равновесия всей системы в целом она рассматривается как абсолютно твердое тело, поэтому в эти уравнения не войдут силы взаимодействия между отдельными телами системы.

2 Силы, которыми тела системы действуют друг на друга, в соответствии с аксиомой о действии и противодействии (третий закон Ньютона), равны по модулю и направлены по одной прямой в противоположные стороны.

3 Если внешняя сила приложена к точке контакта исследуемых тел, ее следует относить только к одному из тел системы.

3.2 Пример решения задачи

О равновесии системы тел

Составная рамная конструкция, части которой соединены шарниром в точке С, находится в равновесии под действием указанных на рисунке 3.1 силовых факторов. Определить реакции внешних связей и значение силы взаимодействия между частями конструкции.

Дано:

Определить: реакции связей.

Решение.

1 Рассматриваем равновесие правой части рамы (рисунок 3.2). На нее действует пара сил с моментом М. Распределенную нагрузку, изменяющуюся по линейному закону, заменяем равнодействующей силой 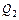, которую прикладываем на расстоянии CD /3 от точки C. Ее численное значение

.

2 Расставляем векторы сил реакций механических связей. Реакцию гладкой поверхности направляем перпендикулярно этой поверхности. Для цилиндрического шарнира указываем две составляющие реакции – горизонтальную 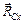и вертикальную .

3 Изображаем систему отсчета: ось Ox направляем горизонтально, ось Oy – вертикально.

4 Силы, действующие на правую часть конструкции, не сходятся в одной точке, поэтому составляем три уравнения равновесия.

(3.1)

(3.2)

. (3.3)

Замечание. Момент силы найден с использованием теоремы Вариньона. Для этого сила была разложена на две составляющие: , .

5 Рассмотрим равновесие левой части конструкции. На нее действуют активная сила и равномерно распределенная нагрузка с интенсивностью q, которую заменяем сосредоточенной силой , приложенной в центре прямоугольника, изображающего эту нагрузку (рисунок 3.3).

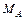6 Связи на левую часть рамы наложены в точках А и С. Для заделки в точке А указываем две составляющие реакции – горизонтальную и вертикальную и момент заделки . Реакция шарнира С включает две составляющие и . В соответствии с аксиомой о действии и противодействии они равны по значениям и противоположны по направлениям силам 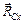и (см. рисунок 3.2).

7 На левую часть составной конструкции действует произвольная плоская система сил, поэтому составляем три уравнения равновесия:

(3.4)

(3.5)

(3.6)

Замечание. Здесь сразу учтено, что ; .

8 Решая полученную систему уравнений (3.1)–(3.6), находим неизвестные реакции связей.

Из уравнений (3.3), (3.1), (3.2) последовательно получаем:

.

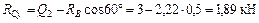Из уравнения (3.4) имеем

Уравнение (3.5) дает

Из уравнения (3.6) находим

9 Для проверки правильности решения рассмотрим равновесие всей системы в целом. На расчетной схеме (рисунок 3.4) помимо активных сил показываем силы реакций внешних связей: заделки в точке А и опоры в точке В. Внутренние силы в точке С компенсируют друг друга и поэтому на схеме не показаны. Реакцию разложим на две составляющие (см. рисунок 3.2).

Подставляя в них численные значения, имеем:

(верно);

(верно);

(верно).

Поскольку получены верные равенства, то расчет выполнен правильно.

10 Находим равнодействующие сил реакций заделки и цилиндрического шарнира:

 

Условие задания С-3

Определение реакций связей рамной конструкции

Рассчитать реакции внешних и внутренних связей конструкций, изображенных на рисунке 3.5. Исходные данные взять из таблицы 3.1.

 

Таблица 3.1 – Исходные данные к заданию С–3

номер варианта	F 1, кН	F 2, кН	q 1, кН/м	q 2max, кН/м	M, кН·м		номер варианта	F 1, кН	F 2, кН	q 1, кН/м	q 2max, кН/м	M, кН·м
										1,1	1,1
			1,6							1,8
			1,8	1,5						0,8
			1,2	1,8
			1,6							1,6	1,4
				0,8							1,1
				1,4							2,4
			1,6							1,8
			3,2
			1,2							0,8
			1,1	3,2						1,6
			1,4	2,2						1,1	2,4
			2,2	1,8						1,8	2,5
			1,5							1,2	2,4
			1,6							1,7	1,2