Из хорошо известной Вам области знаний подберите содержательный пример простого категорического (атрибутивного) суждения вида А (по логическому квадрату). Укажите составляющие его элементы: кванторное слово, субъект, предикат, субъектно-предикатную связку. Сформулируйте другие простые категорические суждения, которые с А находятся в отношении: подчинения (I), контрадикторности (О), контрарности (Е). Укажите истинностные значения I, О, Е для двух истинностных значений А. Дайте анализ распределённости терминов в рассмотренных суждениях А, I, О, Е. Осуществите в отношении выбранного Вами суждения А логические операции превращения, обращения, противопоставления предикату. Проведите анализ распределённости терминов в образовавшихся в результате этих операций суждениях.
Все врачи должны уметь писать рецепты.
Кванторное слово «все».
Термин-субъект, выраженный словосочетанием «врачи».
Термин-предикат, выраженный словосочетанием «должны уметь писать рецепты».
Утвердительная предицирующая связка, не имеющая в данном предложении словесного выражения.
Субъект распределён, предикат не распределён.
Условия совместимости и несовместимости суждений устанавливаются в так называемом логическом квадрате.
1. Все врачи должны уметь писать рецепты
2. Ни один врач не умеет писать рецепты
3. Некоторые врачи должны уметь писать рецепты
4. Некоторые врачи не должны уметь писать рецепты
Превращение
Ни один врач не умеет писать рецепты.
Врач – распределен, умеет писать рецепты – не распределен.
Обращение
Если все врачи – должны уметь писать рецепты, лишь некоторые должны уметь писать рецепты существа - врачи.
Врачи – распределен, должны уметь писать рецепты существа – не распределен.
Противопоставление предикату
Все неврачи не умеют писать рецепты.
Неврачи – распределен, умеют писать рецепты – не распределен.
Противность (контрарность): А<=>Е. Контрарность есть отношение наибольшей противоположности. Суждение ни один врач не умеет писать рецепты является полным отрицанием суждения все врачи должны уметь писать рецепты, поскольку оба эти суждения подразумевают все предметы, включенные в класс, то есть всех людей. Но несовместимость их не является максимальной: общеутвердительное и общеотрицательное суждения могут быть одновременно ложными. Если истинно суждение некоторые врачи должны уметь писать рецепты (которого достаточно для опровержения суждения ни один врач не умеет писать рецепты) или суждение некоторые врачи не должны уметь писать рецепты (опровергающее суждение все врачи должны уметь писать рецепты), то соответствующие общеутвердительное и общеотрицательное суждения окажутся ложными.
Противными являются противоположные общеутвердительное и обще-отрицательное суждения. Из истинности каждого из них следует ложность другого, но из ложности одного не следует ложность другого; противные суждения не могут быть одновременно истинными, но могут быть одновременно ложными.
Подчинение (субординация): A<=>І, E<=>O. Если истинно суждение все врачи должны уметь писать рецепты, то явно истинно суждение некоторые врачи должны уметь писать рецепты; если истинно суждение ни один врач не умеет писать рецепты, то истинно суждение некоторые врачи не должны уметь писать рецепты. Но если истинно суждение некоторые врачи должны уметь писать рецепты, то суждение все врачи должны уметь писать рецепты может быть как истинным, так и ложным; если истинно суждение некоторые врачи не должны уметь писать рецепты, то суждение ни один врач не умеет писать рецепты может также быть истинным и ложным. Если суждение все врачи должны уметь писать рецепты ложно, то суждение некоторые врачи должны уметь писать рецепты может быть как истинным, так и ложным; если ложно суждение ни один врач не умеет писать рецепты, то суждение некоторые врачи не должны уметь писать рецепты может быть как истинным, так и ложным.
Подчиненными являются частные суждения по отношению к соответствующим общим. Ложность частного суждения влечет за собой ложность общего, истинность общего суждения влечет за собой истинность частного, но не наоборот. Подчиняющее и подчиненное суждения могут быть вместе истинными и вместе ложными.
Противоречивость (контрадикторность): А<=>О, Е<=>І. Чтобы опровергнуть суждение все врачи должны уметь писать рецепты, достаточно показать, что некоторые врачи не должны уметь писать рецепты; равным образом истинность суждения некоторые врачи должны уметь писать рецепты опровергает суждение ни один врач не умеет писать рецепты. Если истинны суждение некоторые врачи должны уметь писать рецепты и суждение все врачи должны уметь писать рецепты, то суждение ни один врач не умеет писать рецепты ложно. Если истинны суждения некоторые врачи должны уметь писать рецепты и некоторые врачи не должны уметь писать рецепты, то суждения ни один врач не умеет писать рецепты и все врачи должны уметь писать рецепты также будут ложными. Если суждение некоторые врачи должны уметь писать рецепты ложно, то ложным будет суждение все врачи должны уметь писать рецепты, а, следовательно, суждение ни один врач не умеет писать рецепты будет истинным, как и суждение некоторые врачи не должны уметь писать рецепты.
Противоречащими являются общие и противоположные им частные суждения. Истинность одного противоречащего суждения влечет за собой ложность другого и наоборот. Противоречащие суждения не могут быть вместе ни истинными, ни ложными.
Подпротивность (субконтрарность): І<=>O. Если некоторые врачи умеют писать рецепты, то должны уметь писать рецепты будут некоторые врачи при условии, что ложны суждения все врачи должны уметь писать рецепты и ни один врач не умеет писать рецепты. Если некоторые врачи не должны уметь писать рецепты, то должны уметь писать рецепты будут некоторые врачи при условии, что ложны суждения все врачи должны уметь писать рецепты и никто из врачей не умеет писать рецепты. Если же ложно суждение некоторые врачи умеют писать рецепты, то суждение некоторые врачи не умеют писать рецепты ложным быть не может, потому что в таком случае оказалось бы ложным и суждение ни один врач не умеет писать рецепты. Ибо если ложно, что ни один врач не умеет писать рецепты и ложно, что все врачи должны уметь писать рецепты, то по крайней мере некоторые врачи обязательно должны уметь писать рецепты.
Приведите содержательные примеры основных видов сложных суждений (по одному для каждого вида - отрицания, конъюнкции, дизъюнкции, строгой дизъюнкции, импликации, эквиваленции). Укажите составляющие их суждения. Дайте анализ истинностных значений указанных сложных суждений в функции от истинностных значений их составляющих.
Отрицанием высказывания A называется высказывание, которое истинно, когда A ложно, и ложно, если A истинно. Обозначение: 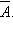 Читается: «неверно, что A».
Читается: «неверно, что A».
Данное определение записывают с помощью таблицы истинности, в которой буква «И» означает истинное высказывание, а буква «Л» – ложное.
| A | И | Л |
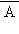
| 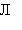
| 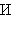
|
Например: отрицанием высказывания {через две точки можно провести две прямые} является высказывание {через две точки нельзя провести две прямые}. Отрицанием высказывания {число 37 не делится на 2} будет высказывание {число 37 делится на 2}.
Конъюнкцией двух высказываний A и B называется высказывание, которое истинно в том и только в том случае, если истинны оба высказывания. Таблица истинности имеет вид:
| A | И | И | Л | Л |
| B | И | Л | И | Л |
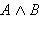
| 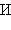
| 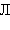
| 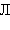
| 
|
Например: конъюнкцией высказываний {3 < 8} и {8 < 11} является высказывание {3 < 8 < 11}. Или, конъюнкцией высказываний {точка A лежит на прямой a} и {точка A лежит на прямой b} является высказывание {точка A лежит на прямой a и на прямой b}.
Дизъюнкцией двух высказываний A и B называется высказывание, которое ложно тогда и только тогда, когда ложны оба высказывания. Обозначение: 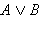 , читается: «A или B». Таблица истинности имеет вид:
, читается: «A или B». Таблица истинности имеет вид:
| A | И | И | Л | Л |
| B | И | Л | И | Л |
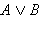
| 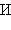
| 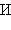
| 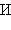
| 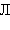
|
Примеры: дизъюнкцией высказываний
{3 < 8} и {3 = 8} является высказывание {3 < 8 < 11};
{точка A лежит на прямой a} и {точка A лежит на прямой b} является высказывание {точка A лежит на прямой a или на прямой b}, где связка "или" не имеет разделительного смысла. То есть точка A может лежать либо только на прямой a, либо только на прямой b, либо же на прямой a и прямой b одновременно.
Свойство 16.9.
Операции дизъюнкции и конъюнкции коммутативны.
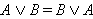 и и 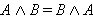 . .
|
Операции дизъюнкции и конъюнкции ассоциативны.
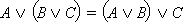 и и 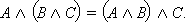
|
Высказывание 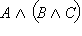 истинно только если одновременно истинны A, B и C, а во всех других случаях – ложно. Высказывание истинно только если одновременно истинны A, B и C, а во всех других случаях – ложно. Высказывание 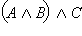 также истинно, только если A, B и C одновременно истинны. Совпадение истинности двух высказываний доказывает их эквивалентность. Аналогично высказывание также истинно, только если A, B и C одновременно истинны. Совпадение истинности двух высказываний доказывает их эквивалентность. Аналогично высказывание 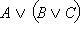 ложно, только если ложны одновременно все три высказывания A, B и C, но в этом случае ложно и ложно, только если ложны одновременно все три высказывания A, B и C, но в этом случае ложно и 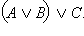 Во всех остальных случаях оба высказывания Во всех остальных случаях оба высказывания 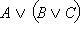 и и 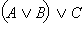 – истинны. Следовательно, – истинны. Следовательно, 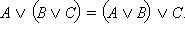
|
Пусть 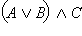 – истинно. Это возможно, только если истинны C и – истинно. Это возможно, только если истинны C и 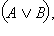 а это значит, что C – истинно, а A и B не являютя одновременно ложными. Отсюда следует, что истинным является одно из двух высказываний а это значит, что C – истинно, а A и B не являютя одновременно ложными. Отсюда следует, что истинным является одно из двух высказываний 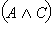 или или 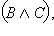 то есть то есть 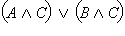 – истинно. Далее, если – истинно. Далее, если 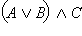 – ложно, то C и – ложно, то C и 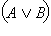 не являются одновременно истинными, то есть либо C ложно, либо ложно не являются одновременно истинными, то есть либо C ложно, либо ложно 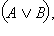 или либо ложно C, либо ложны одновременно A и B. Отсюда одновременно ложны или либо ложно C, либо ложны одновременно A и B. Отсюда одновременно ложны 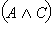 и и 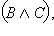 то есть ложно то есть ложно 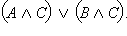 Следовательно, высказывания по определению равносильны и справедливо равенство Следовательно, высказывания по определению равносильны и справедливо равенство 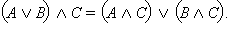 Пусть
Пусть 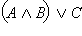 – истинно. Тогда истинно либо C, либо – истинно. Тогда истинно либо C, либо 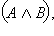 то есть либо истинно C, либо одновременно истинны A и B. В любом случае тогда истинны то есть либо истинно C, либо одновременно истинны A и B. В любом случае тогда истинны 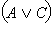 и и 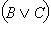 одновременно, а значит, истинно одновременно, а значит, истинно 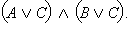 Если же Если же 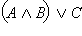 – ложно, то одновременно ложны и C, и – ложно, то одновременно ложны и C, и 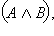 то есть C – ложно, а A и Bне являются одновременно истинными (либо A ложно, либо B ложно). Тогда ложно либо то есть C – ложно, а A и Bне являются одновременно истинными (либо A ложно, либо B ложно). Тогда ложно либо 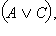 либо либо 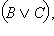 то есть то есть 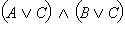 – ложно. Отсюда – ложно. Отсюда 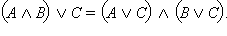
|
Свойство 16.12.
Дизъюнкция любого высказывания A и его отрицания 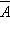 – тождественно истинна. Обозначение:
– тождественно истинна. Обозначение: 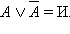
Высказывание «если A, то B» называют импликацией высказываний A и B, если оно ложно лишь в случае, когда A – истинно, а B – ложно. Обозначение: 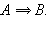 Таблица истинности имеет вид:
Таблица истинности имеет вид:
| A | И | И | Л | Л |
| B | И | Л | И | Л |
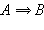
| 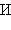
| 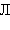
| 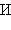
| 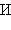
|
Высказывание A называют условием, а B – заключением импликации.
Для любых двух высказываний A и B справедливо
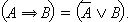
|
Импликацией, обратной данной импликации 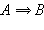 , называется импликация
, называется импликация 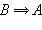 .
.
Импликацией, противоположной данной импликации 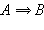 , называется импликация
, называется импликация 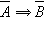 .
.
Например: импликацией высказываний {100 делится на 4} и {100 – четное число} является высказывание {если 100 делится на 4, то 100 – четное число}. Импликация обратная данной будет тогда такой: {если 100 – четное число, то 100 делится на 4}. Как мы видим, если импликация истинна, то обратная к ней не всегда будет истинна. Противоположной к исходной будет импликация {если 100 не делится на 4, то 100 не является четным числом}.
Эквиваленцией высказываний A и B называется высказывание, которое истинно, когда оба высказывания A и B истинны или оба ложны. Обозначение: 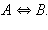 Таблица истинности имеет вид:
Таблица истинности имеет вид:
| A | И | И | Л | Л |
| B | И | Л | И | Л |
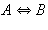
| 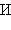
| 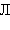
| 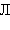
| 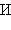
|
Например: эквиваленцией двух высказываний {точки A и B лежат в разных полуплоскостях от прямой a} и {отрезок AB пересекает прямую a} является высказывание {точки A и B лежат в разных полуплоскостях от прямой a тогда и только тогда, когда отрезок AB пересекает прямую a}.
Приведите четыре содержательных примера простого категорического силлогизма (по одному примеру для каждой фигуры; модусы любые). Для каждого примера дайте его логический анализ: укажите модус, термины, распределённость терминов, большую и меньшую посылки (их вид), обоснуйте правильность вывода, используя ссылки на известные правила простого категорического силлогизма.
Ни один ленивый человек не сдаёт экзамены (большая посылка)
Некоторые студенты сдают экзамены (меньшая посылка)
Некоторые студенты не ленивы (заключение)
Модус - Ни один ленивый человек не сдаёт экзамены.
Термины – ленивый человек, экзамены, студенты.
Термин ленивый человек распределён.
Термин студенты не распределен.
Все информативные вещи полезны (большая посылка)
Некоторые сайты не полезны (меньшая посылка)
Некоторые сайты не информативны (заключение)
Модус - Все информативные вещи полезны
Термины – информативные вещи, сайты, информативны
Термин информативные вещи распределён.
Термин сайты не распределен.
Все фрукты питательны (большая посылка)
Все фрукты вкусны (меньшая посылка)
Некоторые вкусные продукты питательны (заключение)
Модус - Все фрукты питательны
Термины – вкусные продукты, фрукты
Термин фрукты распределён.
Термин вкусные продукты не распределен.
Некоторые кружки красивы (большая посылка)
Все кружки полезны (меньшая посылка)
Некоторые полезные вещи красивы (заключение)
Модус - Некоторые кружки красивы
Термины – кружки, полезные вещи.
Термин кружки распределён.
Термин полезные вещи не распределен.
Посылки силлогизма разделяются на большую (которая содержит предикат заключения) и меньшую (которая содержит субъект заключения). По положению среднего термина силлогизмы делятся на фигуры, а последние по логической форме посылок и заключения — на модусы. Данные силлогизмы соответствуют правилам построения.
Приведите содержательный пример энтимемы. Произведите восстановление энтимемы и дайте её логический анализ (аналогично п. 4).
Этот физический процесс не является испарением, так как не происходит перехода вещества из жидкости в пар.
Суждение, стоящее после слов «так как», является посылкой. В энтимеме пропущена большая посылка:
Испарение есть процесс перехода вещества из жидкости в пар.
Этот физический процесс не есть процесс перехода вещества из жидкости в пар.
Этот физический процесс не есть испарение.
Модус - испарение есть процесс перехода вещества из жидкости в пар.
Термины – испарение, физический процесс.
Термины не распределёны.
Большая посылка - Испарение есть процесс перехода вещества из жидкости в пар
Меньшая посылка - физический процесс не есть испарение.
Данный категорический силлогизм построен по II фигуре; особые правила ее соблюдены, так как одна из посылок и заключение отрицательные, большая посылка общая, представляющая собой определение понятия «испарение».






