Математичне забезпечення операцій на грошовому ринку
Основні умовні позначення
i (%) – проста річна ставка відсотка;
i – відносна проста річна ставка відсотка;
iс – відносна величина річної ставки складних відсотків;
j – номінальна ставка складних відсотків;
Ir – сума відсоткових грошей, виплачених на рік за відсотками;
I – загальна сума відсоткових грошей, сплачена за ставкою відсотка за весь період нарахування;
D (%) – проста річна облікова ставка;
d – відносна величина простої облікової ставки;
dс (%) – складна річна облікова ставка;
dс – відносна величина складної річної облікової ставки;
f – номінальна річна облікова ставка;
Dr – сума відсоткових грошей, сплачених на рік за обліковою ставкою;
D – загальна сума відсоткових грошей, сплачених за обліковою ставкою за весь період нарахування;
Р – величина початкової вкладеної грошової суми;
S – нарощена сума;
kн – коефіцієнт нарощення у випадку простих відсотків;
kн.с – коефіцієнт нарощення у випадку складних відсотків;
kн.у – коефіцієнт нарощення у випадку облікових ставок;
k¶ – коефіцієнт дисконтування;
n – період нарахування в роках;
¶ – період нарахування в днях;
К – тривалість року в днях;
ar – річний темп інфляції;
a – темп інфляції;
ia – ставка відсотків, яка враховує інфляцію;
Sa – сума, покупна спроможність якої з урахуванням інфляції дорівнює покупній спроможності суми S при відсутності інфляції;
IH – індекс інфляції;
R – величина кожного платежу ануїтету (фінансова рента);
A – сучасна величина ануїтету;
kH.а – коефіцієнт нарощення ануїтету;
a – коефіцієнт приведення ануїтету;
N – номінальна вартість акції або облігації;
Po – вартість покупки облігації;
Pk – курс облігації;
I0 – дохід за облігацією;
Pa – вартість покупки акції;
Q – ціна продажу акцій;
Ia – дохід за акціями.
Декурсивний та антисипативний способи нарахування відсотків
Існує дві концепції і, відповідно, два способи визначення і нарахування процентів.
Антисипативний (попередній) спосіб. Відсотки нараховуються на початку кожного інтервалу нарахування. Сума процентних грошей визначається виходячи із нарощеної суми:
S = P/(1 – i)n.
Відсотковою ставкою буде виражене у відсотках відношення суми прибутку, що сплачується за певний інтервал, до величини нарощеної суми, яка отримується в кінці цього інтервалу. Ставка, що визначається таким способом, називається (в широкому розумінні) обліковою ставкою або антисипативним відсотком.
Декурсивний спосіб. Відсотки нараховуються в кінці кожного інтервалу нарахування. Декурсивна відсоткова ставка або позичковий відсоток – це відношення суми нарахованого за певний інтервал доходу до суми, що є на початку даного інтервалу.
У світовій практиці декурсивний спосіб найбільш розповсюджений. У нас – антисипативний, особливо в періоди високої інфляції. При рівності позичкового відсотку та облікової ставки, нарощення початкової суми в другому випадку (антисипативний спосіб) йде швидше, тому в літературі часто можна зустріти твердження, що декурсивний спосіб більш вигідний для позичальника, а антисипативний – для кредитора. Але це справедливо лише для невеликих відсоткових ставок.
Приклад. Початкова сума боргу складає 3800 грн. Визначити величину нарощеної суми через 4 роки при застосуванні декурсивного і антисипативного способів нарахування відсотків. Річна ставка – 70 %.
Декурсивний спосіб:
S = 3800 (1 + 0,7)4 = 31738.
Антисипативний спосіб:
S = 3800 / (1 – 0,7)4 = 475 000.
Даний приклад демонструє різницю у результатах при різних способах нарахування відсотків на фоні великих сум і високих відсоткових ставок.
Прості ставки позичкових відсотків (декурсивних) застосовуються у короткотермінових фінансових операціях, коли інтервал нарахування співпадає з періодом нарахування (і складає, як правило, термін менше одного року). Звичайно, прості ставки позичкових відсотків можуть застосовуватись і в будь-яких інших випадках за домовленістю сторін, що беруть участь в угоді.
Залежно від способу визначення тривалості фінансової операції розраховується точний або звичайний (комерційний) відсоток. Точний відсоток отримують, коли за часову базу приймають фактичну кількість днів на рік (365 або 366) і точну кількість днів позички. Дата видачі та дата погашення позички завжди рахуються як один день.
У практиці банків різних країн термін у днях і розрахункова кількість днів на рік при нарахуванні відсотків визначається по-різному. Н імецька практика підрахунку кількості днів засновується на тривалості року в 360 днів і місяців у 30 днів. При французькій практиці тривалість року приймається рівною 360 дням, а кількість днів на місяць береться рівною їх фактичній календарній тривалості (28, 29, 30 і 31 день відповідно). В англійській практиці рік береться тривалістю у 365 днів і відповідна точна тривалість місяців. При використанні простих відсотків сума процентних грошей протягом всього терміну боргу визначається виходячи із початкової суми боргу, незалежно від кількості періодів нарахування та їх тривалості.
Основні формули:
відносна величина ставки позичкового відсотка:
i(%) =  100 %; (1.1)
100 %; (1.1)
коефіцієнт нарощення:
kн =  ; (1.2)
; (1.2)
нарощена сума S (операція компаудингу):
S = P (1 + ni); (1.3)
S = P (1 +  i); (1.4)
i); (1.4)
сучасна величина Р (операція дисконтування):
P = 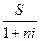 ;
;
період нарахування:
n =  ; (1.5)
; (1.5)
відсоткова ставка:
i =  . (1.6)
. (1.6)
Для випадків простих облікових ставок. При антисипативному способі нарахування відсотків сума отримуваного доходу розраховується виходячи із суми, що отримується після закінчення певного інтервалу нарахування (тобто із нарощеної суми). Ця сума і вважається величиною отримуваного кредиту (або позички). Так як у даному випадку відсотки нараховуються на початку кожного інтервалу нарахування, позичальник, звичайно, отримує цю суму за вирахуванням процентних грошей (S - P). Така операція називається дисконтуванням за обліковою ставкою, а також комерційним або банківськім обліком.
Дисконтом називається дохід, отриманий за обліковою ставкою, тобто різниця між розміром кредиту і сумою, що видається.
На практиці облікові ставки застосовуються, в основному, при обліку (купівлі) векселів та інших грошових зобов’язань.
Відносна величина простої облікової ставки:
d =  ; (1.7)
; (1.7)
нарощена сума S:
S =  =
= 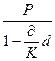 ; (1.8)
; (1.8)
сучасна величина Р нарощеної суми:
P = S (1 - nd) (1.9)
період нарахування:
n =  ; (1.10)
; (1.10)
значення облікової ставки:
d =  . (1.11)
. (1.11)
Складні ставки позичкових відсотків. Якщо після чергового інтервалу нарахування дохід (нараховані за даний інтервал відсотки) не виплачується, а додається до грошової суми, що є на початку цього інтервалу, то для визначення нарощеної суми застосовують формули складних відсотків, які є досить розповсюдженим сьогодні видом відсоткових ставок, що застосовуються у різних фінансових операціях.
Коли виникає можливість вибору між низькою складною відсотковою ставкою і більш високою простою, слід віддавати перевагу першому варіанту.
S = P (1 + ic)n ; (1.12)
S = P (1 + j/m)mn(1 + Ij/m) (нарахування відсотків m раз на рік); (1.13)
S = Pcjn (безперервне нарахування відсотків); (1.14)
коефіцієнт нарощення:
kн,с = (1 + ic)n (1.15)
коефіцієнт нарощення для строку позики, яка не є цілим числом:
kн,с = (1 + ic)na(1 + nbic); (1.16)
сучасна величина Р нарощеної суми:
P =  = Sk
= Sk  ; (1.17)
; (1.17)
відсоткова ставка:
і =  - 1; (1.18)
- 1; (1.18)
номінальна відсоткова ставка:
j = m ( ; (1.19)
; (1.19)
період нарахування:
n =  ; (1.20)
; (1.20)
n =  ; (1.21)
; (1.21)
У нашій країні на даний момент найбільш розповсюдженим є нарахування відсотків за півріччями, поквартальне і щомісячне. Такі відсотки, що нараховуються з певною періодичністю, називаються дискретними.
У світовій практиці часто застосовується також неперервне нарахування складних відсотків (тривалість інтервалу нарахування прагне до нуля, а m – до нескінченності): e = 2/71828…… S = P ejn
Для випадку складних облікових ставок
Нарощена сума S:
S =  ; (1.22)
; (1.22)
S =  (для нарахування відсотків m раз на рік);
(для нарахування відсотків m раз на рік);
коефіцієнт нарощення:
kн,у =  ; (1.23)
; (1.23)
коефіцієнт нарощення для періоду нарахування, що не є цілим числом:
kн,у =  ; (1.24)
; (1.24)
початкова грошова сума Р:
P = S (1-dc)n; (1.25)
період нарахування:
n =  (1.26)
(1.26)
n =  ; (1.27)
; (1.27)
складна облікова ставка:
dc = 1 -  ; (1.28)
; (1.28)
номінальна облікова ставка:
f = m (1 –  ). (1.29)
). (1.29)
Формули еквівалентності облікових ставок. Оскільки умови нарахування відсотків є одним з основних факторів при виборі банку або фінансової компанії для розміщення засобів, необхідно їх порівнювати за деяким загальним показником. У якості такого показника використовується еквівалентна (ефективна) річна ставка простих або складних відсотків.
Еквівалентні відсоткові ставки – це такі ставки різного виду, застосування яких при різних початкових умовах дає однакові фінансові результати.
 i =
i =  ; (1.30)
; (1.30)
d =  ; (1.31)
; (1.31)
i = [(1 + ic)n – 1]/n; (1.32)
ic =  ; (1.33)
; (1.33)
i = 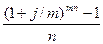 ; (1.34)
; (1.34)
J = m ( ). (1.35)
). (1.35)
Отримана за формулою (1.36) річна ставка складних відсотків, еквівалентна номінальній відсотковій ставці, називається ефективною ставкою складних відсотків.
ic = (1 + j/m)m – 1; (1.36)
j = m ( ); (1.37)
); (1.37)
ic =  . (1.38)
. (1.38)
Визначення індексу інфляції. Відношення ^s/s, що виражене у відсотках, називається рівнем інфляції. При розрахунках використовують відносну величину рівня інфляції – темп інфляції – a.
Величину (1 + а), що показує, у скільки разів sа більше за s (тобто у скільки разів у середньому виросли ціни), називають індексом інфляції іі.
ii= (1 + dr)na×(1 + nbdr)(якщо відомо річний темп інфляції);(1.39)
ii = (1 + am)m (якщо відомо темп інфляції за короткий інтервал). (1.40)
Ін = (1 + dr)na (1 + nadr) (якщо відомий річний темп інфляції); (1.41)
Ін = (1 + am)m (якщо відомий темп інфляції за короткий інтервал). (1.42)
Формула Н. Фішера:
 . (1.43)
. (1.43)
Для визначення відсоткових ставок, враховуючи інфляцію, використовують формули:
i  =
=  ; (1.44)
; (1.44)
 ; (1.45)
; (1.45)
ica =  ; (1.46)
; (1.46)
 ; (1.47)
; (1.47)
dca = 1 –  ; (1.48)
; (1.48)
 . (1.49)
. (1.49)
Для нарощеної суми ануїтету. При погашенні кредиту частинами поточне значення суми боргу буде після чергової сплати зменшуватись, і відповідно, буде зменшуватись сума відсотків, що нараховується на черговому інтервалі.
Розмір сплати в кінці першого року:
S1 = D/n + Dg; (1.50)
D – сума кредиту;
g – річна ставка відсотків за кредитом у відносних одиницях.
Залишок боргу в кінці другого року становитиме:
D2 = D – D/n = D (1 – 1/n). (1.51)
Розмір сплати в кінці другого року становитиме:
S2 = D/n + Dg = D/n + Dg (1 – 1/n). (1.52)
Залишок боргу на початок третього року становитиме:
D3 = D – D/n = D (1 – 2/n) і т. д. (1.53)
Сума виплачених відсотків буде дорівнювати:
I = Dg + D2g + ….. + Dng = Dg (1+ 1 – 1/n + 1 – 2/n +….+ 1 – {(n –1)/n}. (1.54)
Застосувавши до виразу в дужках формулу для суми членів геометричної прогресії, отримуємо:
I = Dg  [(n + 1)/2]. (1.55)
[(n + 1)/2]. (1.55)
Загальна сума погашення кредиту буде дорівнювати:
S = D + I = D (1 + g (n +1)/2]. (1.56)
Якщо внески на погашення кредиту будуть здійснюватись p раз на рік, сума сплачуваних відсотків, визначена аналогічно, буде дорівнювати:
I = [(D/p)g]  [(np +1) / 2]. (1.57)
[(np +1) / 2]. (1.57)
Якщо умовами кредитної угоди передбачено, що кредит і відсотки за ним погашаються протягом його терміну рядом платежів за вказаною в угоді схемою, суму відсотків і загальну суму, що повинна бути погашена, можна визначити, послідовно використовуючи наведені вище формули.
Кредити можуть погашатись однаковими терміновими сплатами, що включають погашення основної суми боргу і виплату відповідної суми відсотків. Якщо відсотки за кредит нараховуються за простою ставкою, загальна їх сума I буде визначатись наведеною вище формулою (1.57).
Загальна сума витрат з погашення кредиту в розмірі D буде дорівнювати:
S = D + I, (1.58)
і, відповідно, розмір однакових термінових сплат буде дорівнювати:
R = (D + I)/np; (1.59)
де n – термін кредиту в роках;
p – кількість сплат на рік.
При погашенні рівними терміновими сплатами довгострокових кредитів з нарахуванням відсотків за складною ставкою відсотків розміри термінових сплат можуть бути визначені, якщо перерахувати (перевести) суми сплат до моменту видачі кредиту, або, інакше кажучи, здійснювати їх дисконтування з використанням формули
P = S/(1 + i)n = Skd; (1.60)
де kd – коефіцієнт дисконтування (приведення);
kd = 1/(1 + i)n. (1.61)
Якщо платежі розміром R будуть здійснюватись щорічно в кінці кожного року, то їх значення, дисконтовані за складною ставкою відсотків i на початок першого року виплат, будуть дорівнювати:
A1 = R / (1 + i),
A2 = R / (1 + i)2,
до цих формул ….
An = R/(1+i)n. (1.62)
Застосувавши до суми цих величин формулу для суми членів геометричної прогресії, отримуємо для сучасної (наведеної) величини суми всіх платежів наступне вираження:
t = 1,
A = å At = R [1 – (1 + i) –n] / i, (1.63)
t = n.
Із цієї формули можна визначити розмір платежу:
R = Ai / [1 – (1 + i)-n]. (1.64)
Оскільки сума всіх платежів з погашення кредиту і нарахованих відсотків повинна бути рівною сумі кредиту D, розмір сплат, що вносяться в кінці кожного року при ставці складних відсотків i за формулою (1.64) буде дорівнювати:
R = D i/[1 – (1 + i)-n]. (1.65)
Загальна сума погашення кредиту складе:
S = nR = nD i/[1 – (1 + i)-n]. (1.66)
А сума сплачених відсотків буде дорівнювати:
I = S – D. (1.67)
Якщо рівнозначні виплати за кредитом у розмірі R будуть вноситись p раз на рік, їх розмір, що визначається аналогічно, складе:
R = D [(1 + i)1/p – 1] / [1 – (1 + i)-n]. (1.68)
S = R 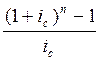 . (1.69)
. (1.69)
Для сучасної величини ануїтету:
A = R  . (1.70)
. (1.70)
Для коефіцієнта нарощення ануїтету:
kн,а =  . (1.71)
. (1.71)
Для коефіцієнта приведення ануїтету:
 . (1.72)
. (1.72)
Для визначення розміру чергового платежу:
R =  ; (1.73)
; (1.73)
R =  . (1.74)
. (1.74)
Для визначення терміну ануїтету:
n = 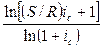 ; (1.75)
; (1.75)
n =  . (1.76)
. (1.76)
Для визначення доходу за акціями:
 . (1.77)
. (1.77)
Для визначення дохідності покупки акцій у вигляді складної ставки позичкового відсотка:
ic 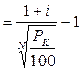 . (1.78)
. (1.78)
Для визначення дохідності покупки облігацій у вигляді складної ставки позичкового відсотка:
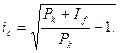 (1.79)
(1.79)






