Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
(1).
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c - сжатым. В случае, когда a=b=c, эллипсоид представляет собой сферу.
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
, (2)
. (3)
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), - двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
, (4)
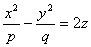, (5)
где p и q - положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), - гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q, параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).
Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).
Выберем какую-нибудь плоскость; обозначим ее буквой 
. Зададим, кроме того, некоторое положительное число q. Пусть М - произвольная точка пространства, не лежащая на плоскости , 
- основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой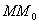 
в новое положение 
так, чтобы имело место равенство
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.
Пусть дана некоторая поверхность F; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F’. Будем говорить, что поверхность F’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).
ПРИМЕР. Доказать, что произвольный трехосный эллипсоид
может быть получен из сферы
в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия 
и к плоскости Oxz с коэффициентом сжатия 
.
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть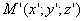 
- точка, в которую переходит при этом точка 
. Выразим координаты x’, y’, z’ точки М’ через координаты x, y, z точки М. Так как прямая MM’ перпендикулярна к плоскости Oxy, то x’=x, y’=y. С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то 
.
Таким образом, мы получаем искомые выражения:
, 
, (6)
или
, 
, 
(7)
Предположим, что M(x; y; z) - произвольная точка сферы
.
Заменим здесь x, y, z их выражениями (7); получим
,
откуда
.
Следовательно, точка M’(x’; y’; z’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам
, 
, 
;
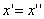тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.
Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.
Однополостный гиперболоид
имеет две системы прямолинейных образующих, которые определяются уравнениями:
, 
;
, 
,
где и 
- некоторые числа, не равные одновременно нулю. Гиперболический параболоид
также имеет две системы прямолинейных образующих, которые определяются уравнениями
, 
;
, 
.
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L. Точка S называется вершиной конуса; линия L - направляющей.
Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).
