Для студентов ИНЭК (заочное отделение)
Курс, II семестр
КРИТЕРИИ ОЦЕНКИ
Билет к зачету состоит из 4 заданий:
1. Вопрос по теории
2. Задача по теории вероятностей
3. Задача по теории вероятностей
4. Задача по математической статистике
Оценка «Зачтено» ставится в случае правильного выполнения двух заданий билета.
В случае Зачета с оценкой:
«Удовлетворительно» - правильное выполнение двух заданий билета.
«Хорошо» - правильное выполнение трех заданий билета и собеседование по написанной работе.
«Отлично» - правильное выполнение четырех заданий билета и собеседование по написанной работе.
.
Вопросы для подготовки к ЗАЧЕТУ
ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
1. Предмет Теории вероятностей (ТВ), объект изучения ТВ. Понятия события, опыта, элементарных исходов опыта. Элементы комбинаторики: размещения, перестановки, сочетания.
2. Совместные, несовместные, противоположные события. Полная группа событий. Алгебраические операции над событиями: сумма, произведение, разность.
3. Классическое определение вероятности. Свойства вероятности. Статистическая и геометрическая вероятности.
4. Основные теоремы ТВ: теоремы сложения и умножения вероятностей.
5. Гипергеометрическое распределение.
6. Формула полной вероятности. Формула Байеса.
7. Повторение испытаний, схема Бернулли. Формула Бернулли. Возможные постановки задач с применением схемы Бернулли.
8. Локальная и интегральная теоремы Муавра-Лапласа.
9. Случайная величина (СВ). Дискретные СВ (ДСВ). Операции над СВ.
10. Числовые характеристики ДСВ: математическое ожидание М(х) и его основные свойства; дисперсия D(x) и ее свойства; среднеквадратическое отклонение 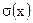 .
.
11. Основные понятия и определения математической статистики.
12. Эмпирическая функция распределения F*(Х) и её свойства. Полигон частот, гистограмма.
13. Точечные оценки параметров распределения: несмещенные и смещенные оценки для генеральной средней и генеральной дисперсии (формулы).
Рекомендуемая литература
1. Сборник задач по высшей математике для экономистов. Под редакцией Ермакова В.И. М., 2002.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистики. М., 2001.
ПРИМЕРЫ ЗАДАЧ
Элементы теории вероятностей.
Найти вероятности указанных событий, пользуясь правилами сложения и умножения вероятностей:
| вариант | |
| 1. | Для сигнализации об аварии установлены три независимо работающих датчика. Вероятность исправной работы 1-го датчика равна 0,9, второго 0,95, третьего 0,8. Найти вероятность того, что: а) сработает только один датчик; б) сработает только два датчика; в) сработает хотя бы один датчик. |
| 2. | Три стрелка производят по одному выстрелу в цель независимо друг от друга. Вероятности попадания в цель для каждого из них равны соответственно 0,7; 0,8; 0,9. Найти вероятность того, что: а) в цель попадает только один стрелок; б) в цель попадает только два стрелка; в) в цель попадает хотя бы один стрелок. |
| 3. | Вероятность выполнения плана бригадами соответственно равна 0,8 и 0,9. Найти вероятность того, что выполнят план: а) обе бригады; б) хотя бы одна бригада; в) только одна бригада. |
| 4. | Всхожесть семян первого, второго и третьего сортов некоторой культуры составляет соответственно 90%; 80% и 70%. Вычислить вероятность того, что из трех посеянных разносортных семян этой культуры: а) взойдут все три; б) взойдет только одно; в) взойдет хотя бы одно. |
| 5. | Рабочий обслуживает три станка. Вероятность бесперебойной работы в течение месяца для первого станка равна 0,8, для второго -0,9, для тртьего-0,8. Найти вероятность того, что в течение месяца без остановки будут работать: а) все станки; б) только два станка; в) хотя бы один станок. |
| 6. | Вероятность установления в данной местности устойчивого снежного покрова с октября равна 0,1. Определить вероятность того, что в ближайшие три года в этой местности устойчивый снежный покров с октября: а) не установится ни разу; б) установится хотя бы один раз; в) установится два раза. |
| 7. | Исследователь разыскивает нужные ему сведения в трех справочниках. Вероятности того, что эти сведения находятся в первом, во втором и третьем справочниках равны соответственно 0,7; 0,6 и 0,9. Найти вероятность того, что требуемые сведения содержатся: а) только в одном справочнике; б) хотя бы в одном справочнике; в) во всех справочниках. |
| 8. | Всхожесть фасоли 80%, гороха 90%, бобов 70%. Определить вероятность того, что из трех посеянных семян различных культур: а) взойдут два; б) не взойдет ни одного; в) взойдет хотя бы одно. |
| 9. | Вероятность выхода из строя станка в течение одного рабочего дня равна 01. Какова вероятность того, что за три рабочих дня станок: а) ни разу не выйдет из строя; б) выйдет только один раз; в) выйдет хотя бы один раз |
| 10. | Отдел технического контроля поверяет изделия на стандартность. Вероятность того, что наугад взятое изделие окажется бракованным, равна 0,15. Проверено три изделия. Какова вероятность того, что среди них бракованных: а) все три; б) только два; в) хотя бы одно. |
Найти вероятности указанных событий, пользуясь формулами полной вероятности и Байеса:
| вариант | |
| 1. | На фабрике на машинах А, В, С производят соответственно 25; 35 и 40% всех изделий. В их продукции брак составляет соответственно 15; 10 и 5%. 1) Найти вероятность того, что случайно выбранное изделие окажется дефектным. 2) Выбранное изделие оказалось дефектным. Найти вероятность того, что оно изготовлено на машине А. |
| 2. | Всхожесть семян свеклы первой партии 90%, второй партии -80%. Перед посевом смешали 2 ц семян 1-ой партии и 3 ц семян 2-ой партии. 1) Какова будет вероятность всхода, если наугад посадили одно семя? 2) Семя взошло. Какова вероятность того, что оно из 1-ой партии? |
| 3. | На спартакиаду прибыло 20 лыжников, 15 гимнастов и 5 шахматистов. Вероятность выполнить квалификационную норму такова: для лыжника -0,8; для гимнаста -0,6; для шахматиста -0,9. Случайно вызывается один спортсмен. 1) какова вероятность того, что он выполнит норму? 2) Спортсмен выполнил норму. Какова вероятность того, что это был шахматист? |
| 4. | На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 3% брака, второй -2%, а третий -4%. 1) Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000, со второго -2000 и с третьего -2500 деталей. 2) Деталь оказалась бракованной. Найти вероятность того, что она изготовлена на третьем автомате. |
| 5. | На одном заводе на каждые 100 лампочек приходится в среднем 10 нестандартных, на втором -15, а на третьем -20. Продукция этих заводов составляет соответственно 50; 30 и 20% всех электролампочек, приобретаемых жителями района. 1) Найти вероятность того, что приобретенная лампочка будет стандартной. 2) Приобретенная лампочка оказалась стандартной. Какова вероятность того, что эта лампочка изготовлена на первом заводе? |
| 6. | Три оператора радиолокационной установки производят соответственно 25; 30 и 40 % всех измерений, допуская 5,4 и 3 % ошибок. 1) Найти вероятность того, что случайно проверенное измерение окажется ошибочным. 2) Измерение оказалось ошибочным. Найти вероятность того, что оно произведено первым оператором. |
| 7. | На ферме содержатся 40% коров костромской породы и 60% башкирской. В районе эпидемия ящура. Вероятность заболеть ящуром у коров костромской породы 0,6; у коров башкирской породы -0.7. Для обследования случайным образом взята одна корова. 1) Найти вероятность того, что она больна ящуром. 2) Корова оказалась больна. Какова вероятность того, что она башкирской породы. |
| 8. | В засуху растение погибает с вероятностью 0,9. Без засухи выживаемость растения составляет 95%. Вероятность засухи в году данной местности 0,2. 1) Найти вероятность выживания растения в данном году. 2) Растение выжило. Найти вероятность того, что засухи не было. |
| 9. | Имеется два мешка семян одной культуры первой партии, всхожестью 90% и один мешок той же культуры второй партии, всхожестью 85%. Наугад взяли мешок и посадили одно зерно. 1) Какова вероятность того, что оно взойдет? 2) Зерно взошло. Какова вероятность того, что оно из первой партии? |
| 10. | Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго -0,03, для третьего -0,04. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего в два раза меньше, чем второго. Из ящика наудачу взята одна деталь. 1) Какова вероятность того, что деталь будет бракованной? 2) деталь оказалась бракованной. Какова вероятность того, что она произведена на первом станке? |






