Задание 2. Решение уравнений методом дихотомии и методом Ньютона.
Определить корень двумя указанными методами с точностью поиска ε=0.01
Таблица 3.
| Вар | Метод дихотомии[1] (после уравнения задан начальный интервал); | Метод Ньютона (после уравнения задана начальная точка приближения). |
 X∈ [1;2] X∈ [1;2]
| 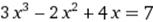 X0=3 X0=3
| |
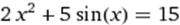 X∈ [2;3] X∈ [2;3]
|  X0=3 X0=3
| |
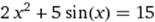 X∈ [2; 3] X∈ [2; 3]
| 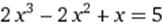 X0=3 X0=3
| |
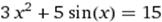 X∈ [1;2] X∈ [1;2]
|  X0=3 X0=3
| |
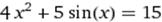 X∈ [1;2] X∈ [1;2]
| 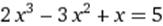 X0=3 X0=3
| |
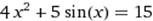 X∈ [1;2] X∈ [1;2]
|  X0=3 X0=3
| |
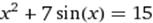 X∈ [4;5] X∈ [4;5]
| 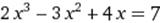 X0=3 X0=3
| |
 X∈ [4;5] X∈ [4;5]
|  X0=3 X0=3
| |
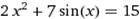 X∈ [2;3] X∈ [2;3]
|  X0=3 X0=3
| |
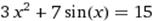 X∈ [1; 2] X∈ [1; 2]
| 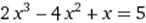 X0=4 X0=4
| |
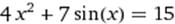 [1; 2] [1; 2]
| 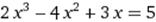 X0=3 X0=3
| |
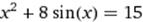 X∈ [4; 5] X∈ [4; 5]
| 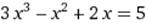 X0=3 X0=3
| |
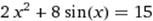 X∈ [1; 2] X∈ [1; 2]
| 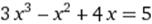 X0=2 X0=2
| |
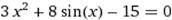 X∈ [1; 2] X∈ [1; 2]
| 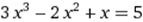 X0=3 X0=3
| |
 X∈ [1; 2] X∈ [1; 2]
| 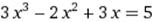 X0=3 X0=3
| |
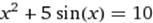 X∈[3; 4] X∈[3; 4]
|  X0=4 X0=4
| |
 X∈[1;2] X∈[1;2]
| 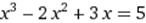 X0=3 X0=3
| |
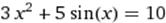 X∈[1; 2] X∈[1; 2]
| 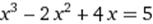 X0=3 X0=3
| |
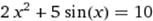 X∈[1;2] X∈[1;2]
| 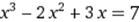 X0=4 X0=4
| |
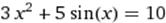 X∈[1; 2] X∈[1; 2]
| 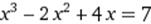 X0=3 X0=3
| |
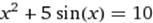 X∈[3; 4] X∈[3; 4]
| 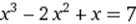 X0=4 X0=4
| |
 X∈ [1; 2] X∈ [1; 2]
| 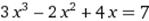 X0=3 X0=3
| |
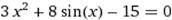 X∈ [1; 2] X∈ [1; 2]
| 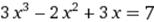 X0=3 X0=3
| |
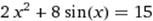 X∈ [1; 2] X∈ [1; 2]
| 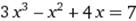 X0=2 X0=2
| |
 X∈ [4; 5] X∈ [4; 5]
|  X0=3 X0=3
| |
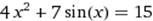 [1; 2] [1; 2]
| 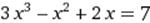 X0=3 X0=3
| |
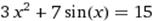 X∈ [1; 2] X∈ [1; 2]
| 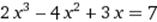 X0=3 X0=3
| |
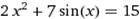 X∈ [2;3] X∈ [2;3]
| 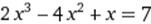 X0=4 X0=4
| |
 X∈ [4;5] X∈ [4;5]
| 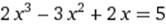 X0=3 X0=3
| |
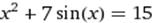 X∈ [4;5] X∈ [4;5]
|  X0=3 X0=3
| |
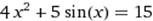 X∈ [1;2] X∈ [1;2]
|  X0=3 X0=3
| |
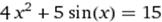 X∈ [1;2] X∈ [1;2]
| 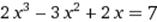 X0=3 X0=3
| |
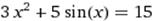 X∈ [1;2] X∈ [1;2]
| 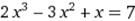 X0=3 X0=3
| |
 X∈ [2; 3] X∈ [2; 3]
|  X0=3 X0=3
| |
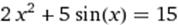 X∈ [2;3] X∈ [2;3]
| 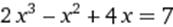 X0=3 X0=3
| |
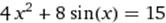 X∈ [1;2] X∈ [1;2]
|  X0=3 X0=3
|
Задание 3. Модели систем массового обслуживания. Метод Монте-Карло.
В трехканальную систему массового обслуживания с отказами поступает пуассоновский поток заявок. Время между поступлениями двух последовательных заявок распределено по показательному закону 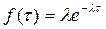 , λ – постоянная. которая задана для конкретного варианта в таблице 6. Длительность обслуживания каждой заявки равна 1 мин. Найти методом Монте-Карло математическое ожидание а числа обслуженных заявок за время T = Т мин (задается в таблице 6).
, λ – постоянная. которая задана для конкретного варианта в таблице 6. Длительность обслуживания каждой заявки равна 1 мин. Найти методом Монте-Карло математическое ожидание а числа обслуженных заявок за время T = Т мин (задается в таблице 6).
Случайные числа выбираются ПО СТРОКАМ из варианта в таблице 2 (из задания 1) таким образом: НАЧИНАТЬ С МЕСТА ПЕРЕСЕЧЕНИЯ строки с номером предпоследней цифры зачетной книжки студента и столбца с номером последней цифры. (В таблице выделено первое случайное число для 36-го варианта).
Заполнить таблицу:
Таблица 5.
| Но-мер заявки i | Слу-чай-ное число ri | -ln (ri) | Время между двумя последовательными заявками
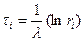
| Момент поступления заявки
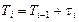
| Момент
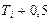 окончания обслуживания заявки каналом
окончания обслуживания заявки каналом
| Счетчик | |||
| Обслуженных заявок | Отказов | ||||||||
Варианты для интенсивностей λ и времен:
Таблица 6.
| В1 | В2 | В3 | В4 | В5 | В6 | В7 | В8 | В9 | В10 | В11 | |
| λ | |||||||||||
| T, мин | |||||||||||
| В12 | В13 | В14 | В15 | В16 | В17 | В18 | В19 | В20 | В21 | В22 | |
| λ | |||||||||||
| T, мин | |||||||||||
| В23 | В24 | В25 | В26 | В27 | В28 | В29 | В30 | В31 | В32 | В33 | |
| λ | |||||||||||
| T, мин | |||||||||||
| В34 | В35 | В36 | |||||||||
| λ | |||||||||||
| T, мин |
Задание 4. Задача линейного программирования
Выбор оптимального парка самолетов с учетом тактико-технических характеристик, воздушного сообщения, количества пассажиров описывается задачей линейного программирования. Оптимизировать количество рейсов в месяц и затраченных расходов на маршруте в месяц. Решить графически задачу. Вариант в соответствии с последними цифрами зачетки.
Таблица 7.
Вар 1
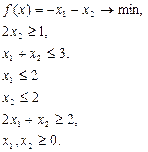
| Вар 2
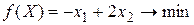 , ,
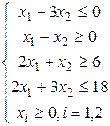
|
Вар 3
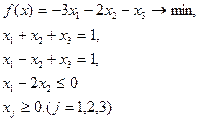
| Вар 4
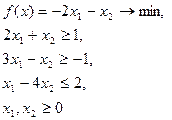
|
Вар 5
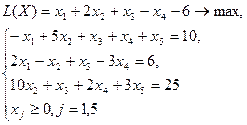
| Вар 6
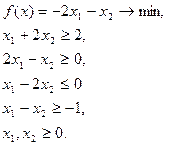
|
Вар 7
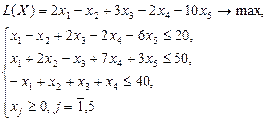
| Вар 8
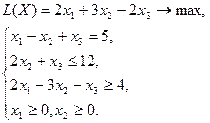
|
Вар 9

| Вар 10
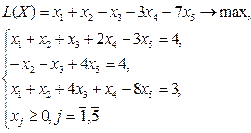
|
Вар 11

| Вар 12

|
Вар 13

| Вар 14

|
Вар 15
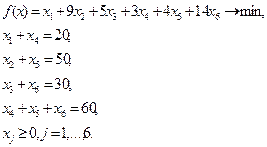
| Вар 16

|
Вар 17
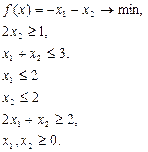
| Вар 18
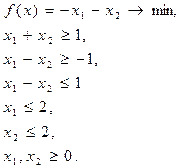
|
Вар 19
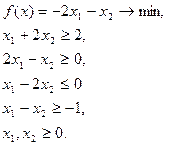
| Вар 20
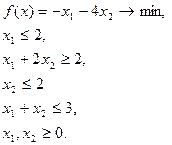
|
Вар 21

| Вар 22
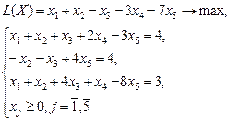
|
Вар 23
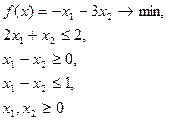
| Вар 24
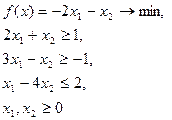
|
Вар 25

| Вар 26
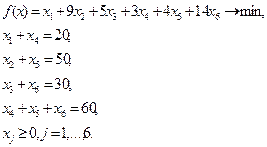
|
Вар 27
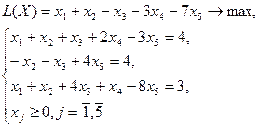
| Вар 28

|
Вар 29

| Вар 30
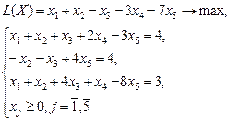
|
| Вар 31 | Вар 32 |
Вар 33

| Вар 34
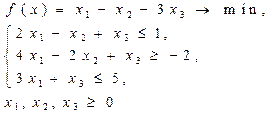
|
Вар 35
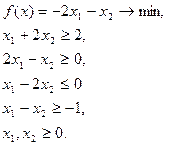
| Вар 36
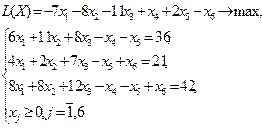
|
Литература
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.:Учеб. Пособие для студентов вузов. – М.: Высш.шк.,2000. (Часть 4. Моделирование случайных величин методом Монте – Карло, параграф 6, параграф 7).– задания 1 и 3.
2. Турчак Л. И., Плотников П. В. Основы численных методов: Учебное пособие. —
2-е изд., перераб. и доп. —М.: ФИЗМАТЛИТ, 2003. —304 с. —ISBN 5-9221-0153-6. (Задание 2)
3. Вентцель Е.С. Исследование операций: задачи, принципы, методология. – М.,Наука,1988. (Глава 3.Линейное программирование, Глава 6. Теория массового обслуживания; Статистическое моделирование случайных процессов(Метод Монте-Карло))
Все перечисленные книги можно найти в интернете.
Номер варианта по последним цифрам зачетки.




