Дәрістің мазмұны:
1 Өлшеудің қателіктерін метрологиялық түрде топтау үлгісі.
2 Қателіктердің түрлеріне берілген анықтамалар.
3 Статистикалық қателіктерді Гаусс заңын табуда қолдану.
Дәрістің мақсаты: өлшеудің қателіктерін бір-бірінен айыра білу және оларды табудың жолдарын игеру.
Өлшеу еш уақытта дәл болмайды. өлшеудің дәлдігінің ықтималдығы нолге тең. Метрология өлшеу қателіктерінің келесі топтау үлгісін береді.
2.1 Сурет – Өлшеу қателіктерін топтау үлгісі
Жалпы айтқанда өлшеудің қателігі – алған өлшемнің нәтижесінің дұрыс болмауы. Өлшеу қателігі физикалық шаманы өлшегенде болатын қателіктердің барлық құрамын қамтиды, сонан кейін алынған нәтиженің шын не нақты мәндерден аутқуын көрсетеді. Мысалы, физикалық шаманың өлшенген мәні Х десек, ал оның шындық мәнін Хш деп белгілесек, сонда ауытқу (отклонение) мынаған тең.
. (2.1)
Физикалық шаманың шындық мәні дегеніміз, өлшеу қателігі жоқ деген сөз. Бұл сөз идеалдық түрде айтылған сөз. Тәжірибе жүзінде ФШ шындық мәнін алуға болмайды. Сондықтан практикада ФШ шын мәнінің Хш орнына оның нақты Хн мәнін қолданады. ФШ-ның нақты мәнін табу үшін ерекше әдістерді және үлгілі өлшеуіш құралдарды қолданады.Сонда былай жазуға болады.
. (2.2)
Бұл алгебралық айырмашылық таңбасын өзгерту мүмкіндігінен мұны өлшеудің абсолюттік қателігі деп атайды. Сондықтан өлшеудің дұрыс нәтижесі.
. (2.3)
Кей кезде түзелу коэффициентін қолданады.
. (2.4)
Сонда өлшеудің дұрыс мәні былайша жазылады.
. (2.5)
Белгілі ғылыми деректерге негізделе отырып өлшеу қателіктерін үш топқа бөлуге болады: тұрпайы, жүйелілік және кездейсоқтық қателіктер. Тұрпайы қателіктерге электрөлшеуіш аспаптың көрсеткішін дұрыс бағаламау жатады. Оған аспаптың шкаласының бөліктерін қате бағалау, немесе көпшкалалы аспаптың еселеу коэффициенттерін дұрыс қолданбау жатады. Немесе, көрсеткішті қарағанда тіл мен шкаланың арасында болатын параллаксты елемеу. Сыртқы ортаның өлшеуіш аспапқа күшті әсері, оның бұзылуымен және кездейсоқ кедергілер өлшеудің тұрпайы қателіктеріне әкеліп соғады.
Абсолюттік мәні және таңбасы белгілі қателіктерді жүйелі қателіктер деп атайды. Егер өлшеу процесі тұрақты жағдайда өткізілсе, оларда тұрақты мәнде болады. Егер өлшеу жағдайы заңды түрде өзгерсе, жиелі қателіктер не өзгермейді, не өзгерсе заңды түрде өзгереді.
Жүйелі қателіктерге қандай өлшеу қателіктері жатады? Олар: электрөлшеуіш аспаптың қателігі, қолданылған өлшеу әдістемесінің қателігі, өлшеуіш құралдың қателігі, аз мәнді елемегендіктің қатесі және сыртқы ортаның әсерінен қателік. Осы қателіктерді жеке-жеке қарастырайық.
Электрөлшеуіш аспаптың жүйелі қателігіне үш топ қателіктер жатады: аддитивті, пропорционалды және шкаланы бөлу қателіктері. Егер өлшеуіш аспаптың тілі бастапқы кезде шкаланың нолінде тұрмаса аддитивтік қателік пайда болады. Бұл қателікті, егер аспаптың шкаласы бірқалыпты болса, алгебралық қосумен түзетуге болады. Пропорционалдық қателіктер көрсетуші аспаптарда қолданатын қосымша кедергілер мен шунттардың өз мәнінен ауытқуына байланысты.Егер бұл ауытқулардың мәндері белгілі болса, алынған өлшеудің нәтижесін түзеу коэффициентіне көбейтіп, пропорционалдық қателіктерді түзеуге болады. Шкаланы бөлу қателіктерін әр өлшеуіш аспапқа қосымша түзету таблицасын жасап жоюға болады. Ол таблицаларды жасағанда өлшеуіш аспаптарға қарағанда өлшеу дәлдігі жоғары өлшеуіш құралдар қолданылуы қерек. Қолданылған өлшеу әдістемесі мен өлшеуіш құралдың қателіктері кернеу көзінің электр қозғалыс күшін (э.қ.к.-эдс) өлшейтін вольтметрдің ішкі кедергісінің әсерінен пайда болады. Аз мәнді елемегендіктің қатесі өлшеу әдістемесі мен өлшеуіш құралдың қателіктеріне жақын. Ол қатені өлшеу кезінде де, өлшегеннен кейінде табуға болмайды. Себебі, оның неден пайда болатын факторларды да табу не білу қиын.
Егер сыртқы ортаның әсеріне келсек, ол температураның, атмосфералық қысымдықтың және ауаның ылғалдылығына байланысты. Осы жағдайлар өлшеуіш аспаптың көрсетуінің туралығына әсерін тигізеді. Және сыртқы электр не магнит өрістерінің өзгеруі де өлшеу нәтижесіне қосымша қателік кіргізеді.
Практикалық өлшеулерде жүйелі қателіктерді құрал-сайманмен және әдістемелік қателіктердің алгебралық қосындысы деп санайды
. (2.6)
Әр уақытта жүйелік қателікпен бірге кездейсоқтық қателіктер болады. Сондықтан өлшеудің абсолюттік қателігі мынаған тең
. (2.7)
Мұнда Δқ.с. – кездейсоқтық қателік. Осы қателіктің екі құраушылардың әсерімен бір физикалық шама көп рет қайталап өлшегенде, мысалы nрет, статистикалық қатар пайда болады
. (2.8)
Мұндай қатарға орташа арифметикалық мән (значение) аламыз
. (2.9)
Әр өлшемнің орташа арифметикалық мәннен ауытқуы орташа квадраттық ауытқумен (ОКА) табылады
. (2.10)
Орташа арифметикалық мән мен орташа квадраттық ауытқу келесі көрсетілетін үлестірімнің қалыпты (нормальное) заңының (Гаусс заңы) сипаттамалары болып есептеледі
. (2.11)
Мұнда Р(х)-әр физикалық шаманың болу ықтималдығының тығыздығы. Бұл аналитикалық мағынаны ықтималдық тығыздықтың қисығымен көрсетуге болады:
2.2 Сурет – Ықтималдық тығыздықтың қисығы
Бұл суретте көрсетілгендей ықтималдық тығыздықтың қисығында ең үлкен ординат болып өлшемдердің орташа мәні саналады, яғни өлшеу нәтижелерінің орталық топтасуы болады. Егер Х жүйелік қатеге жатса, ОКА осы нәтижелердің орталық топтасудан ауытқуларын көрсетеді. Ықтималдық теорияда және математикалық статистикада үш сигманың (3 
x)ережесі бекітілген. Сонда кез келген өлшемнің нәтижесі Рс=0.9973 сенімділік ықтималмен 
3 x екі арада жатады, демек
(2.12)
мұнда Рс=0.997.
Электроэнергетикада сенімділік ықтимал Рс=0.95 мәнінде алынған, сонда 
екі ара кішірееді
. (2.13)
Pc=0.95.
Бұл мағынаны жалпы түрде былайша жазуға болады
(2.14)
мұнда t = 1,2,3…
Практикалық кезде өлшеу процесін көп уақытқа созуға болмайды. Ең көп болғанда өлшеуді 5 не 8 реттен қайталауға болады. Бұл жағдайда орташа арифметикалық мәннің растылығы артады.
Сондықтан аз рет өлшегенде орташа арифметикалық мәннің орташа квадраттық ауытқымасы былайша табылады
. (2.15)
Сонда орташа арифметикалық мәннің сенімділік арасы мынаған тең
(2.16)
мұнда Pc=0.95, tp,n – Стьюденттің коэффициенті, оны әдетте келесі кестеден табады:
2.1 Кесте
| n | |||||||||
| t0,95,n | 4,3 | 3,2 | 2,8 | 2,6 | 2,4 | 2,3 | 2,1 | 1,96 |
Кейбір кезде физикалық шаманы тура табуға болмайды, ол басқа шамалармен математикалық тәуелділік формулалармен байланысты болады. Мысалы бұл функционалдық байланысты жалпы түрде былай жазуға болады
A=f(x) (2.17)
егер х өлшегенде dx орташа абсолюттік қате жіберсек, онда
A+dA=f(х+dх). (2.18)
Дифференциалдың қасиетіне сәйкес
. (2.19)
Сонда салыстырмалы қателік
. (2.20)
Мұны натурал логарифмнің дифференциалы ретінде жазуға болады
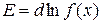. (2.21)
