Опр.
Матрицей системы линейных уравнений (1) называется матрица, состоящая из коэффициентов при неизвестных.
Опр. Расширенной матрицей системы линейных уравнений (1) называется матрица, состоящая из коэффициентов системы и столбца свободных членов.
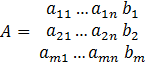
Обозначим за r = rang (A) ранг системы.
= rang (
ранг расширенной матрицы.
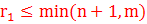
Непонятно что в лекции после этого. Если надо допиши плз)
Я конечно хз надо это или нет, но мне кажется это лишнее, потому что это уже не определение.
Теорема Кронекера - Капелли.
Система линейных уравнений (1) совместна тогда и только тогда, когда ранг матрицы равен рангу расширенной матрицы, т.е. 
= 
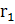
Доказательство:
Необходимость:
Пусть система (1) совместна.
и 
является решением.
b - линейно выражено через 
, следовательно если 
- первая (I) система векторов,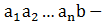 
вторая (II), то отн. эквивал (I)часть (II) и вектор b линейно выражается через .
Значит у этих систем равные ранги 
Достаточность:
Векторы 
являются базисом в (II), значит они линейно независимы, и так как , они являются базисом в системе (II), следовательно вектор b линейно выражается через 
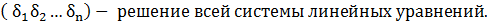
Теорема (Правило решения систем линейных уравнений)
Для того, чтобы решить систему линейных уравнений ранга r необходимо:
1) Выбрать базисный минор и соответствующую ему базисную подсистему.
2) Объявляем свободными переменными неизвестные, не входящие в базисный минор и перенести элементы со свободными переменными в правую сторону.
3) Объявляем свободную переменную параметром и решить систему r-уравнений с r-неизвестными любым методом (Методом Крамера)
Однородные системы линейных уравнений.
Опр. система линейных уравнений вида
называется системой линейных однородных уравнений.
Следствие.
решение системы линейных однородных уравнений
Система линейных однородных уравнений всегда совместна.
Опр. Решение (0...0) нулевое или тривиальное.
Теорема. Критерий наличия нетривиальных решений для системы линейных однородных уравнений.
Однородная система линейных уравнений имеет нетривиальное решение <=> ранг системы < n
Теорема. Сумма двух рангов решений системы.
Очень непонятно в тетради, если можешь напиши.
А у меня там другая теорема: свойство решений систем однородных уравнений о_О
Опр. Фундаментальной системой решений системы линейных однородных уравнений называется базис множества решений L системы однородных линейных уравнений
Опр. Фундаментальной системой решений называется такая линейно независимая система решений, через которую линейно выражаются все решения этой системы.
Опр. Фундаментальной системой решений называется максимальный ЛНЗ набор решений данной системы.
Теорема. Если r- ранг системы линейных однородных уравнений < n неизвестных, то эта система имеет фундаментальную систему решений, состоящую из n-r векторов.
Доказательство:
Пусть базисный минор состоит из первых r-строк и r-столбцов.
....................................................
строим n-r решений
Матрица имеет ранг n-r
пусть b 
- произвольное решение
Решение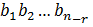 
1.линейно независимое 2.любое решение линейно выражается через них => получили фундаментальную систему решений
Замечание:
Нахождение нормальной фундаментальной системы решений:
1) Найти общее решение системы линейных уравнений.
2) Придать свободным неизвестным значения
(1,0,0),..., (0,0,...,1)
3) По формулам общего решения найти зависимые переменные
4) Объединить зависимые и независимые решения в решение.
