мультиколлениарности между факториальными признаками уравнения регрессии?
3. значение коэффициента парной корреляции равное 0,8
5.Как можно устранить мультиколлениарность между факториальными признаками уравнения регрессии?
1) исключить факториальный признак вызывающий мультиколлениарность;
6.Гетероскедастичность – это ….
1) явление, когда с изменением факториального признака (Х) демперсия случайной компоненты будет увеличиваться или уменьшаться, или изменяться по какому – либо другому закону;
7.Что понимается под дисперсией случайного члена уравнения регрессии ?
3) характеризует тесноту связи функции Y с аргументами Xi, при условии, что прочие не включенные в уравнение регрессии аргументы этой функцией действуют корриляционно независимо от аргумента Xi;
8.Какой вид распределений случайнойго члена уравнения регрессии характерен для гомоскедастичного случая?
1) нормальное распределение кривой;
9. Гетероскедастичность случайного члена уравнения регрессии приводит:
1) с изменением факториального признака (Х) дисперсия случайной компоненты будет увеличиваться или уменьшаться, или измениться по какому – либо закону;
10. Возможный способ снижения влияния гетероскедастичность случайного члена уравнения регрессии на оценки параметров уравнения регрессии:
1) придать наблюдению с малой дисперсией больший вес, а наблюдениям с большой дисперсией меньший вес;
11. При выполнении теста ранговой корреляции Спирмена предполагается:
1) дисперсия случайной составляющей будет либо увеличиваться, либо уменьшаться по мере увеличения Х;
12. Для расчета коэффициента ранговой корреляции Спирмена необходимо упорядочить:
1) данные по Х и абсолютную величину e упорядочивают по возрастанию;
13. Расчет коэффициента ранговой корреляции Спирмена производится по формуле:
 |
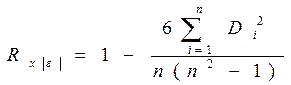1.
14. Тестовая статистика в тесте ранговой корреляции Спирмена определяется по формуле:
2. 
 |
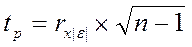
15. Согласно тесту ранговой корреляции Спирмена нулевая гипотеза об отсутствии гетероскедастичности случайного члена уравнения регрессии будет отклонена при уровне значимости в 5 % если тестовая статистика…
2. tр > 1,96;
16. При проведении теста Голдфелда—Квандта предполагается…
2. Что стандартное отклонение σεi распределения вероятности εi пропорционально значению x в этом наблюдении;
17. Для выполнения теста Голдфелда-Квандта имеющиеся наблюдения:
1) упорядочиваются по возрастанию Х
18. В тесте Голдфелда-Квандта Нулевая гипотеза об отсутствии гетероскедостичности будет отклонена, если:
1) Fp>Fт
19. В тесте Голдфелда-Квандта рекомендуемое деление исходной выборки из 30 наблюдений на подвыборки составляет:
1) 3 части
20. При проведении теста Глейзера предполагается:
1) что стандартное отклонение di связано с изменением факториального признака соотношением di=a’+b’*Xig
21. Для нахождения регрессионной зависимости, характеризующей изменение гетероскедастичности случайного члена уравнения регрессии в тесте Глейзера, используется регрессионное уравнение вида:
1. 
.
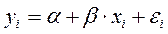22. В тесте Глейзера нулевая гипотеза об отсутствии гетероскедастичности случайного члена уравнения регрессии будет отклонена, если в уравнении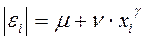 
…
1. величина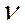 
будет значимо отличаться от 0;
23. Для снижения влияния на оценки уравнения регрессии гетероскедастичности необходимо:
1. разделить коэффициенты уравнения регрессии на параметр, вызывающий гетероскедастичность.
24. Если наличие существенно гетероскедастичности и случайного члена уравнения регрессии ранговой корреляции Спирмена или тестом Голфелда Квандта, то для снижения влияния гетероскедастичнсти на эффективность оценок уравнения регрессии можно каждое наблюдение:
- использовать вместо переменной
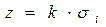, пропорциональной 
;
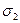25. Если наличие существенной гетероскедастичности случайного члена уравнения регрессии подтверждено тестом Глейзера то для снижения влияния гетероскедастичности на эффективность оценок уравнения регрессии необходимо:
3)в качестве Zi взять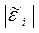 
27. Автокорреляция случайного члена уравнения регрессии – это…
1)зависимость одного члена уравнения от другого.
28. Автокорреляция случайного члена уравнения регрессии приводит к тому, что оценки уравнения регрессии становятся:
2)не эффективными, стандартные ошибки коэффициентов регрессии занижаются.
29. Причиной положительной автокорреляции случайного члена уравнения регрессии обычно является:
3)постоянная направленность воздействия не включенного в уравнение регрессии какого-либо фактора
30. Уравнение,отражающее авторегрессионную схему первого порядка для автокорреляции случайного члена, имеет вид:
1) 
;
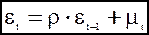31. Оценку коэффициента автокорреляции случайного члена уравнения регрессии из авторегрессионной схемы первого порядка можно осуществить по формуле:
2) 
;
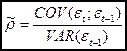32. Расчетное значение d – критерия статистики Дарбина - Уотсона определяется по формуле:
2) 
;
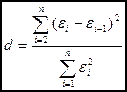33. Значение d – критерия статистики Дарбина – Уотсона в больших выборках связано с коэффициентом автокорреляции случайного члена уравнения регрессии следующим соотношением:
3) 
.
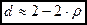№ 34
Почему нельзя составить таблицу с указаниями точных критериев значений D критерия статистики Дарбина – Уотсона?
1) Критическое значение DW зависит от количества объясняющих переменных в уравнении регрессии и от количества наблюдений,зависит еще и от конкретных значений, принимаемых объясняющими переменными.
№ 35
В каком случае нельзя отключить нулевую гипотезу об отсутствии автокорреляции случайного члена уравнения регрессии?
2) если d≥dкрит то нельзя отклонить и ошибки будут некоррелированы
№ 36 По какой формуле пересчитывается значение D критерия статистики Дарбина – Уотсона при отрицательной автокорреляции случайного члена уравнения регрессии?
1) в больших выборках при отрицательной автокорреляции ρ=-1 и dρ≈2-2ρ
№ 37
Как устранить автокорреляцию случайного члена уравнения регрессии, если она описывается авторегрессионной схемой 1 ого порядка?
1) привести её к виду y’t= α*c + β*x’t + μt
38. Для чего используется поправка Прайса-Уинстена?
3) для преобразования модели таким образом, чтобы остатки были некоррелированы.
39. Поправка Прайса-Уинстена равна:
2) 
;
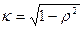40. Для одновременной оценки коэффициента корреляции случайного члена уравнения регрессии и коэффициентов самого уравнения регрессии применяются методы:
3) метод Кохрейна-Оркатта, метод Хилдрета-Лу, метод Дарбина.
41. Метод Кохрейна-Оркатта, используемый для оценки коэффициентов автокорреляции и коэффициентов уравнения регрессии включает следующие этапы:
1) 1. оцениваем исходное регрессионное уравнение, т.е. находим оценки;
2. вычисляем остатки
3. находим оценку коэффициента автокорреляции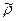 
4. используя данную оценку 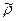находим уравнение, где автокорреляция устранена
5. проводим определение параметров полученного уравнения и находим новые значения оценок
6. повторно вычисляем остатки и фактически возвращаемся к этапу 3
42. Метод Хилдрета-Лу, используемый для оценки коэффициента автокорреляции случайного члена уравнения регрессии и коэффициентов самого уравнения регрессии, заключается в следующем:
1) В данном методе исследователь задает интервал изменения величины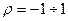 
и шаг. Для каждого значения 
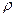производится оценка фактических параметров из уравнения, в котором автокорреляция полностью устранена. Затем выбирается из полученных результатов такой, который дает min стандартную ошибку для преобразования уравнения. Используемые в этом уравнении значения 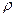и факториальные переменные принимаются за искомые.
43. Какие системы алгебраических уравнений называются системами одновременных уравнений?
1) Уравнения, в которых одни и те же переменные в различных уравнениях используются как объясняющие переменные, так и результирующие переменные.
44. Почему нельзя определить параметры уравнения функции потребления простой кейнсианской модели формирования доходов?
1) Т.к. результирующий признак коррелирует со случайной составляющей. Это приводит к смещению оценок уравнения регрессии.
45 Какие переменные считаются эндогенными переменными?
1) Переменные, которые определяются внутри модели.
46. Какие переменные считаются экзогенными переменными?
1. переменные, заданные вне модели
47. Какие переменные считаются эндогенными переменными?
2. переменные, определяемые внутри модели
48. Какие уравнения называются структурными?
1. уравнения, где описываются сами взаимосвязи между переменными
49. Какие уравнения называются уравнениями в приведенной форме?
1. уравнения, где слева эндогенные переменные, а справа только экзогенные
50. Косвенный метод наименьших квадратов предполагает выполнение следующих процедур:
1) Исходящая структура систем уравнений преобразуются к системе приведенных уравнений и, используя МНК, находим несмещенные оценки коэффициентов приведенной системы уравнений. Используем соотношение между коэффициентами, приведенными в систему уравнений, и структурную систему находим коэффициенты структурной системы уравнений. 51. Идентифицируемая система одновременных уравнений имеет число коэффициентов:
1) число коэффициентов приведенной системы уравнений равно числу коэффициентов исходной структурной системы уравнений
52. Неидентифицируемая система одновременных уравнений имеет число коэффициентов:
1 ) число коэффициентов приведенной системы уравнений меньше числа коэффициентов структурной системы уравнений 53.Сверхидентифицируемая система одновременных уравнений имеет число коэффициентов:
1) число коэффициентов приведенной системы уравнений больше числа коэффициентов структурной системы уравнений
