Направленность химических процессов. Энтропия. Изобарно-изотермический потенциал.
В механических системах самопроизвольно протекают процессы, в которых уменьшается потенциальная энергия, т.е. критерием самопроизвольности служит неравенство Δ E п<0. Для химических процессов имеются аналогичные критерии. В XIX веке таким критерием считали выполнимость условия Δ H <0 (принцип Бертло). Это казалось правдоподобным, т.к. при Δ H <0 (в экзотермической реакции) система переходит в состояние с меньшей энергией. Однако впоследствии было обнаружено много нарушений принципа Бертло(невозможность протекания некоторых экзотермических реакций и возможность – некоторых эндотермических). Поэтому принцип Бертлов настоящее время не применяется. Его нарушение связано с влиянием энтропии.
Состояние вещества можно охарактеризовать двояко: 1) Указать значения измеряемых свойств, например, температуру и давление. Это характеристики макросостояния. 2) Указать мгновенные характеристики каждой частицы вещества – ее положение в пространстве, скорость и направление перемещения. Это характеристики микросостояния.
Поскольку тела состоят из огромного количества частиц, то данному макросостоянию соответствует колоссальное число различных микросостояний. Это число называется термодинамической вероятностью W. С ней связано одно из фундаментальных свойств вещества – энтропия:
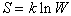 ,
,
где k – постоянная Больцмана.
Энтропию измеряют в Дж/К, а для одного моля – в Дж/(моль·К). Это мера вероятности протекания самопроизвольного процесса в изолированной термодинамической системе. Процесс же наиболее вероятен тогда, когда все молекулы вещества, или элементы системы занимают или займут в результате процесса (одинаковое) энергетическое состояние, при этом станет невозможен никакой дальнейший процесс то есть система станет термодинамически устойчива. Такое состояние не всегда совпадает с наибольшим беспорядком и напротив сам по себе не является устойчивым состоянием он так сказать несёт потенцию - либо достижения ещё большего беспорядка либо увеличения энтальпии то есть порядка в системе. В не изолированных (закрытых), а тем более открытых системах всё ещё сложнее и понятие энтропии там несколько условно. Энтропия - мера экстенсивности термодинамической системы при данном интенсивном факторе которым выступает температура, произведение энтропии на ИЗМЕНЕНИЕ температуры и есть изменение энергии системы. Энтропия может и не меняться тогда как энергия системы изменяться будет. При изотермических процессах составляющая энергии системы в которую входит энтропия равна нолю. Да здесь я только пытаюсь изложить физическое понимание энтропии, применительно к информационным системам смысл энтропии как экстенсивного фактора видимо сохраняется.
Изобарно-изотермический потенциал
Энергия Гиббса - это величина, показывающая изменение энергии в ходе химической реакции и дающая таким образом ответ на вопрос о принципиальной возможности протекания химической реакции; это термодинамический потенциал следующего вида:
G = U+PV-TS
Энергию Гиббса можно понимать как полную химическую энергию системы (кристалла, жидкости и т.д.)
Понятие энергии Гиббса широко используется в термодинамике и химии [1].
Самопроизвольное протекание изобарно-изотермического процесса определяется двумя факторами: энтальпийным, связанным с уменьшением энтальпиисистемы (ΔH), и энтропийным T ΔS, обусловленным увеличением беспорядка в системе вследствие роста её энтропии. Разность этих термодинамических факторов является функцией состояния системы, называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса (G, кДж)






