Інтерлінація функцій двох змінних (мішана інтерполяція).
Інтерлінацією функції 
на системі ліній 
називається відновлення її за допомогою слідів 
, 
.
Приклади інженерних задач, які приводять до інтерлінації.
Картографія дна моря за даними гідролокації. Задача відтворення поверхні дна моря за даними гідролокації, що одержані на різних лініях -- курсах корабля з гідролокатором – є типовою задачею інтерлінації функції двох змінних за даними її слідами на декількох лініях.
Треба побудувати рівняння 
рельєфу дна моря. Тут 
– координати змінної точки на поверхні моря (біжучі координати) в деякій системі координат, вибраній дослідником;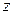 
– віддаль від поверхні моря в точці з координатами 
до дна. Для побудови використовуються сліди 
функції (дані гідролокації) на 
лініях 
– курсах корабля. За вказаними лініями і функціями 
будується функція на оcнові одної із формул кусково-поліноміальної інтерлінації. Ці формули зручні для програмування. Тому побудову функції та її ліній рівня можна доручити бортовій ЕОМ. Вибір курсів корабля визначаєтьcя дослідником.
Наближене відновлення поверхні космічного тіла за даними радіолокації
Задача відновлення поверхні космічного тіла за даними радіолокації виникає не тільки в астрономії. Її ефективне розв'язання може вплинути також на розвиток оборонних технологій тощо. Хай промінь радіолокатора рухається вздовж деякої наперед вибраної дослідником системи ліній на космічному об'єкті, що вивчається (або просто на достатньо віддаленому об'єкті). Промінь відбивається від об'єкта, що дозволяє одержувати віддаль до точки відбиття, тобто значення функції у системі координат 
, вибраній відповідним чином. Тут 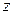– віддаль від точки з координатами на об'єкті до радіолокатора (на вказаних лініях-курсах променя локатора). Обробка такої інформації часто повинна проходити досить швидко і потребує математичного апарату, що найбільш природньо використовує одержувані дані, тобто інтерлінації. Такий підхід можна використати, зокрема, для наближеного опису поверхні Венери, яку не видно через її хмари в оптичний телескоп.
Планування експерименту для відновлення.
На практиці, при плануванні і проведенні експериментів, широко використовується такий підхід. Хай нам треба знайти формулу , що описує деяку характеристику процесу, яка залежить від двох змінних (параметрів)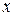 
та 
. Для цього фіксуються значення 
параметра 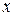і для них знаходяться функції 
(функції 
можуть бути зображені у вигляді графіків, накреслених самописом або наближено, їх значеннями в декількох точках 
). Змінні 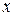та можна поміняти місцями: фіксуємо значення 
параметра і для цих значень 
знаходимо функції 
. Одержана інформація використовується для побудови шуканої функції у вигляді полінома Лагранжа від змінних 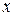та , або у вигляді деякої кусково-поліноміальної функції (сплайна), яка інтерполює дані на вибраній множині вузлів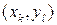 
, або у вигляді згладжуючого сплайна, коефіцієнти якого знаходяться методом найменших квадратів тощо. Важливе те, що на практиці часто використовуються тільки функції або тільки функції 
. Використання інтерлінації дозволяє врахувати функції і функції одночасно, що, природно, дає більш точні наближення до функції .
Бажано проводити експеримент так, щоб знаходити значення функції (або її сліди) не на серії прямих, паралельних осям координат, а на серії прямих (або кривих) більш загального положення. Для обробки такої інформації треба мати математичний апарат наближення з допомогою цієї інформації. Таким апаратом є інтерлінація функцій.
Проектування корпусів літаків, суден, автомобілів
У книжках А. Фокса, М. Пратта [16], М. О. Корнишина, В. Н. Наймушина і В. Ф. Снігирьова [8], Е. А. Стародетко [14] та ін. методи обчислювальної геометрії розробляються для потреб автоматизації проектування машин і механічних систем. До них належить задача проектування корпусів літаків, ракет, суден, автомобілів. У їхню основу, в багатьох випадках, можуть бути покладені інтерлінація та інтерфлетація функцій. У сучасній техніці, особливо в авіа- і суднобудуванні, в космічній техніці, широко використовуються конструкції складної форми, які розраховуються і проектуються як оболонки. При апроксимації і заданні серединних поверхонь цих оболонок зручно використовувати математичний апарат сплайн-інтерлінації та сплайн-інтерфлетації функцій і сплайнів.
