Рассматривая здесь только задачи вытеснения нефти водой из чисто нефтяного пласта, мы с единых позиций подходим к двум основным одномерным моделям вытеснения: модели слоистого пласта (МСП) и модели Баклея-Леверетта (МБЛ). Частично сравнение этих моделей рассматривалось многими авторами, однако ясности в этом вопросе нет до сих пор. Ниже мы покажем, что в случае дебитного описания (говорим «как q-модель») МСП являете более общей, чем МБЛ, тогда как с учетом давления («как р-модель») МБЛ более реально может описывать вытеснение.
------------------------------------------------
1. Основанная на идее использования законов Дарси при поршневом вытеснении в каждом слое пласта с функцией распределения F(K) слоев по проницаемости, К = k / kmax, (k - абсолютная проницаемость, kmax - её максимальное значение), МСП приводит в конечном итоге к определению динамики добычи нефти в терминах безразмерной зависимости
Qн(t)/Qo= T(Q(t)/Qo) (1)
(мы назовем ее T-зависимостью). Здесь Qн(t), Q(t) - количества добытых нефти и жидкости, Q0 — извлекаемые запасы, а функция y = Т(x) = x при x ≤ δ
и параметрически задаётся соотношениями:
у = Гн(ϰ), x = Г(ϰ), ϰ 
[0,1],
при х ≥ δ, где
(ϰ) 
δ=Γн(1)
(ϰ) = (ϰ)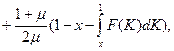 
Отметим, что при известном перепаде давления Δp (t) динамика добычи нефти и жидкости описывается формулами:
Qн (t) = Qo ·Гн (ϰ (t), Q(t) = Q oГ(ϰ(t)),
ϰ(t)= 
, Qo(t) 
, (2)
где µb— вязкость воды, A- площадь поперечного сечения пласта, L - его длина, kВ/k = const.
2. Как легко видеть, функция у = Т(x) однозначно определяется по заданным µ и F(K) и не зависит от режима вытеснения. Более того, сама функция F(K) может быть найдена по известным Т(x) и µ, причем одной и той же Т(x) могут соответствовать различные пары (µ,F(K)). Выбор F(K) в том или ином одно- или многопараметрическом семействе функций, что обычно и практикуется при использовании МСП, эквивалентен выбору Т(x) в соответствующем семействе функций, также в одно- или многопараметрическом.
Особо выделим случай µ= 1, когда Т(x) записывается в явном виде через функцию
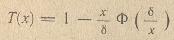
Кроме того, положение x(t,K) фронта ВНК в слое с проницаемостью К определяется в этом случае по формуле:
(3)
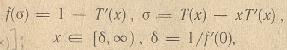3. Хорошо известно, что выходные характеристики МБЛ выражаются также в терминах зависимости (1), и теперь функция Т(x) связана с основным параметром q-модели, функцией Баклея-Леверетта, либо параметрически по формулам:
f(σ)= 1 - Т'(х), σ = Т(х) - хТ'(х),
x Î[δ,∞), δ= 1/f’(0)
либо явно:
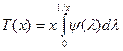
где σ =ψ(λ) — функция, обратная к λ = f'(σ). При этом T(x) ≡ х, если x ≤ δ.
Если расслоить теперь однородный пласт МБЛ в соответствии с функцией распределенияF(K,определяемой равенством
F(K)= 1 – ψ(К/δ), КÎ [0, 1], (4)
то получим совпадение функций Т(х) для МБЛ и МСП с такой функцией распределения и µ = 1. Более того, в силу соответствия
σ = 1 - F(K),f’(σ)=K/δ,
будут совпадать, согласно (3), и распределения водонасыщенности σ для этих двух моделей, что позволяет говорить о полной их эквивалентности. Последнее сравнение и было положено нами в основу обобщения схемы Баклея-Леверетта на многомерные q-модели вытеснения [2]. Вместе с тем отметим, что при µ≠1 даже при совпадении Т(х) для МСП и МБЛ распределения насыщенностей в них не совпадают.
4. В силу сказанного выше ясно, что МСП и МБЛ совершенно аналогично (в терминах Т-зависимости Т(х)) описывают процесс вытеснения при задании дебитов отбора. Однако необходимо отметить, что МСП, в отличие от МБЛ, допускает и случаи невыпуклых вверх функций Т(х), что и делает ее, как q-модель, более общей, чем МБЛ.
Отметим еще, что распределения давления в пласте в этих моделях (в МСП — осредненного по сечению) описываются по-разному: если в МСП оно, как и Т(х), полностью определяется функциейF(K), то в МБЛ необходимо привлекать, помимо f(σ), еще и одну из относительных фазовых проницаемостей. Именно наличие дополнительной функции-параметра и делает МБЛ, как р-модель, более универсальной.
Характеристики вытеснения
Описание технологических показателей разработки для отдельной скважины или участка месторождения проводится часто в терминах Т-зависимостей того или иного семейства, обычно в рамках МСП или МБЛ. Различие методик состоит лишь в способах выбора параметров этих семейств. Используются также и другие зависимости, например, содержащие среди характеристик вытеснения обводненность продукции. Некоторые из простейших подходов такого типа описаны ниже.
1. Определяя обводненность продукции по функциям Qн(t) и Q(t) формулой
(5)
при известной зависимости 
сразу же получаем зависимость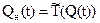 
,
где 
Если f(t) — монотонно возрастающая функция, то вместо формулы (5) легко получаем её интегральный вариант:
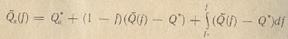
Здесь Qн*, Q*, f *— значения технологических показателей в некоторый момент
времени t= t*, QH(t) =Q~H(f(t)), Q(t) = Q~(f(t)).
Так как обычно стремлению f к единице соответствует неограниченный рост количества добытой жидкости, то в данном описании функция Q(f) в точке f = 1 должна иметь так называемую интегрируемую особенность, т. е. 
должен существовать как несобственный интеграл и равняться извлекаемым запасам Q0. Рассматривая функцию с простейшей особенностью такого вида
,0< а <1
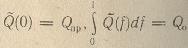и определяя A и α из условий нормировки
, 
,
приходим в итоге к T-зависимости:
 |
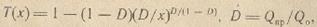Т(х) = 1 - (1 - D)•(D/x)D/(1 – D), D= Qпр/Q0,
широко используемой в методике [4] и полученной в рамках МБЛ по функции f(σ) = 1 - (1 - σ)1/D. Отметим, что в таком случае
.
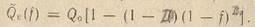
Простейшими обобщениями, отвечающими Q(f) вида
 |
0 < α < 1,
являются двупараметрические зависимости
, (6)
D1 = 1 - α, a = D1/α). Они предложены в [3], где получены из других предположений, и могут быть записаны в более общем виде:
,
,
.
Подчеркнем, что соответствующая (6) функция Баклея-Леверетта не может быть записана явно, но легко указать вид обратной к ней функции.
2. Рассмотрим еще один подход к описанию Т-зависимостей, используя для этого набор стандартных функций Т(x) любого вида, в том числе и вышеприведенных.
Пусть даны возрастающие функции Ti(x) (
) такие, что
Ti(x) ≡ х на [0,Di] и T'i(Di)=1, limTi(x)= 1.
Составляя «выпуклую» комбинацию (ниже суммирование всюду по 1 от 1 до n)
, 
, (7)
при условии 
получаем T-зависимость, удовлетворяющую соотношениям
Т(х) ≡ х, x Î[0,D], T'(D) = 1, T(x) ® 1 при х ® ¥.
Если Тi(х) выпуклые вверх, а ψi (λ.), λ Î[0,1/ Di ] и Fi(K), К Î [0,1] - соответствующие им функции МБЛ и МСП с μ = 1, то Т(x) также выпукла вверх, и отвечающие ей функции ψ(λ) и F(K) определяются формулами
 |
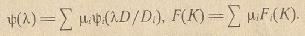, F(K)= 
.
3. Предыдущий подход в рамках МБЛ по физическому смыслу эквивалентен условному разбиению однородного пласта на n пропластков с долей мощности mi,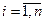 
, в каждом из которых вытеснение происходит по своему закону с функцией Баклея-Леверетта, определяемой по Т(x).
Действительно, формальное суммирование технологических показателей для любых n несообщающихся пропластков, в которых
вытеснение описывается T-зависимостями Тi(х), доля закачки в i-ый пропласток есть величина vi = const, а доля запасов равна μi, и приводит в терминах T-зависимости T(x) для пласта в целом к соотношению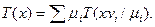 
Сравнение с (7) показывает, что этой формуле соответствует доля закачки в i-ый пропласток, равная μi•Di/D).
4. Запишем теперь размерный аналог (7):
, Mi=μiQ0.
При заданных Т(x) и Qпр задача аппроксимации реальной зависимости (Q(t), Qн(t)) такой линейной комбинацией известных функций по методу наименьших квадратов сводится, как легко видеть, к задаче квадратичного программирования с неизвестными Мi ≥ 0,..., Мn ≥0 и связью. При этом извлекаемые запасы будут определяться по формуле
Динамический вариант этой задачи, когда на различные моменты истории разработки производится пересчет коэффициентов μi = Mi / Qо, можно интерпретировать как изменение во времени долей извлекаемых запасов («перетоки» из пропластка в пропласток) и самих извлекаемых запасов (маложелательный, но «объяснимый» эффект).
Отметим, что число неизвестных параметров при таком подходе к задаче идентификации может ограничиваться только возможностями методов квадратичного программирования.
