РАЗДЕЛ МИКРОЭКОНОМИКА
Лабораторная работа № 1
Спрос и предложение на индивидуальных рынках. Построение паутинообразной модели
I. Цель работы
1. Исследование динамики равновесия сил спроса и предложения.
2. Построение графиков спроса, предложения, паутинообразной модели.
II. Общие сведения
Состояние рыночной экономики, уровень и механизм ее развития описывается с помощью таких понятий, как спрос (D), предложение (S) и способы их координации и приспособления друг к другу.
Обратная зависимость объема спроса от уровня цен фиксируется законом спроса и объясняется следующим:
- снижение цен увеличивает число покупателей;
- насыщение рынка приводит к снижению полезности дополнительных единиц продукта, поэтому покупатели готовы покупать его только по более низким ценам (рис.1.1. а)
Рис. 1.1, а Рис. 1.1, б
Действие ценового фактора приводит к изменению величины спроса (QD), передвигая его вдоль кривой спроса (от т.А к т.В) (рис.1.1,а). Действие неценовых факторов (потребительские вкусы, доход и т.д.) влияет на изменение спроса (D) и приводит к перемещению кривой спроса (от D1 к D2) (рис 1.1,а)
Закон предложения отражает прямую зависимость объема предложения (QS) от цены (Р). Прямая связь между ценой и объемом предложения объясняется действием закона убывающей производительности факторов производства. Изменение цены приводит к изменению величины предложения QS (от т.А к т.В на рис. 1.1,б). Действие неценовых факторов (цены на производственные ресурсы, изменения в технологии производства, налогообложении и т. д.) приводит к изменению в предложении (от S1 к S2 на рис.1.1, б).
Взаимодействие спроса и предложения приводит к формированию равновесной цены (Pe), при которой величины спроса и предложения сбалансированы. Это взаимодействие может происходить по-разному.
На рис. 1.2 представлены кривые спроса (D) и предложения (S). Кривая спроса описывается функцией QD = a – dPt, а кривая предложения –
QS = -c +sP(t – 1),
где Pt – цена в определенный период времени;
Р(t–1) – цена предыдущего периода, на которую ориентировались производители, предполагая, что цены периода t – 1 сохранятся и в период t;
d и s – углы наклона прямых D и S;
a, c – константы.
Рис. 1.2
Производители, ориентируясь на спрос в данный момент времени t и на уровень цен Po этого же времени, определяют на будущее (следующий период) объем предложения Q1, предполагая, что цены останутся прежними (рис.1.3,а). Но между спросом и предложением существует временной лаг, в период которого нет гарантии стабильности цен. Поэтому дефицит, возникающий при Po, ведет к повышению цены до P1 в период времени t1, а цена Po теперь становится ценой периода t – 1(предыдущего периода). Далее, производитель, по-прежнему ожидая, что такой высокий спрос Q1 и уровень цен P1 сохранится и в следующий период t2, предлагает объем Q2, но избыток предложения ведет к падению цены до P2 и т. д.(рис. 1.3,а и 1.3,б)
Рис. 1.3, а
| 
Рис. 1.3, б
|
Таким образом, если предложение (S) эластично, а спрос (D) менее эластичен (
), то рыночная цена будет удаляться от равновесного уровня (рис. 1.3.а). И наоборот, если спрос более эластичен 
> 
, колебания будут затухающими и приведут к равновесию спроса и предложения (рис.1.4, а).
Рис. 1.4, а
| 
Рис. 1.3, б
|
Отклонение рыночной цены от равновесного уровня будет постоянно воспроизводиться, если наклоны прямых спроса и предложения будут равны = , хотя запаздывание в реакции предложения на изменение цен также может привести к нестабильности равновесия.
III. Лабораторное задание
1. С помощью компьютера выполнить тестовый опрос. Директория MICRO\LABWORK\var x. bat.
2. Определить, на каком графике изображен спрос на один и тот же товар в долгосрочном и на каком в краткосрочном периоде?
| 
|
3.Используя данные полученного варианта, решить задачу по следующему плану:
1) Построить прямые спроса и предложения.
2) Определить аналитически и графически равновесный объем (QE) и равновесную цену (Pe).
3) Рассчитать уровень рыночной цены в любой момент времени t (0 
t 6) по формуле
и построить паутинообразную модель.
4) Начертить график динамики равновесия.
Правильное выполнение задачи оценивается в 1 балл.
Для демонстрации процесса построения использовать программу из директории C:\MICRO\LABWORK\PAUTINE, в которой функции спрос и предложение представлены с помощью следующих обозначений:
где, а и b – константы функций;
А, В – углы наклона прямых D и S;
Pt – цена в определенный период времени;
P(t-1) – цена предыдущего периода.
IV. Содержание отчета
Отчет по лабораторной работе составляется каждым студентом.
Отчет должен соответствовать следующим требованиям:
1 Тему и вариант работы.
2. Цель работы.
3. Расчет и результаты выполнения лабораторной работы.
4. Графическое решение задачи.
5. Вывод по работе.
6. Количество баллов, набранных при тестовом опросе.
V. Варианты к лабораторной работе
1. D = 400 - 1.4 P, S = -20 + 1.2 P, P0 = 40.
2. D = 410 - 1.4 P, S = -30 + 1.2P, P0 = 60.
3. D = 420 - 1.4 P, S = - 10 + 1.2 P, P0 = 70.
4. D = 430 - 1.4 P, S = - 40 + 1.1 P, P0 = 80.
5. D = 380 - 1.3 P, S = -20 + 1.2 P, P0 = 100.
6. D = 390 - 1.3 P, S = -40 + 1.1P, P0 =100.
7. D = 400 - 1.3 P, S = -30 + 1.1 P, P0 =120.
8. D = 410 - 1.3 P, S = -20 + 1.2 P, P0 = 50.
9. D = 420 - 1.3 P, S = -40 + 1.1 P, P0 = 130.
10. D = 400 -1.4 P, S = -20 + 1.2 P, P0 = 120.
11. D = 410 -1.4 P, S = -20 + 1.2 P, P0 = 50.
12. D = 400 -1.4 P, S = -30 + 1.2 P, P0 = 60.
13. D = 400 - 1.4 P, S = -20 + 1.2 P, P0=80.
14. D = 410 - 1.3 P, S = -30 + 1.1 P, P0 = 60.
15. D = 400 - 1.4 P, S = -20 + 1.2 P, P0 = 70.
Лабораторная работа №2
Теория потребительского поведения. Анализ кривых безразличия
I. Цель работы
1. Исследование основных положений теории потребительского поведения.
2. Построение графиков экономического поведения потребителей.
II. Общие сведения
Потребительское поведение рассматривается с позиций предельной полезности (MU) и кривых безразличия.
Предельная полезность (MU) означает прирост общей полезности (TU) на каждую потребленную единицу товара (Q)
.
С каждой дополнительной единицей потребляемого товара прирост общей полезности (TU) уменьшается – в этом заключается закон убывающей предельной полезности, лежащий в основе закона спроса (рис. 2.1).
Рис. 2.1
Потребитель, в соответствии с собственными предпочтениями и ограниченным доходом, стремится приобрести такой набор товара, который позволил бы ему максимально удовлетворить потребности. Это возможно лишь при соблюдении правила максимизации полезности: предельные полезности потребляемых товаров (MU1 и MU2) в расчете на одну денежную единицу (Р) одинаковы и равны
.
Каждая кривая безразличия графически отображает множество наборов товаров, обладающих одинаковой полезностью для потребителя (рис. 2.2).
Кривая безразличия демонстрирует уменьшающуюся предельную норму замещения (MRS). MRS означает, что одно благо (Y) может быть заменено другим (X) без изменения общей величины полезности для потребителя.
Уменьшается MRS в результате приобретения единицы товара Х за счет отказа от приобретения товара Y (движение вниз по кривой безразличия) (рис. 2.2).
Множество кривых безразличия составляет карту безразличия, на которой каждая кривая представляет различный уровень полезности (рис. 2.2).
Для определения потребительского оптимума необходимо рассмотреть линию бюджетного ограничения (С). Линия бюджетного ограничения, как и кривая безразличия, отражает множество комбинаций двух продуктов, но уже в пределах потребительского бюджета (рис. 2.2).
Рис. 2.2
Таким образом, кривые безразличия (U) характеризуют предпочтения потребителя («что хочу»), а бюджетная линия (С) определяет его возможности («что могу»).
Потребитель достигает максимального удовлетворения своих потребностей (потребительский оптимум) в точке касания линии бюджетного ограничения и кривой безразличия (точки 
), где 
товаров 
и 
равна обратному соотношению их цен (рис. 2.3).
Рис. 2.3
Через все точки потребительского равновесия при различных уровнях дохода проходит линия «доход - потребление» (G), имеющая положительный наклон для нормальных товаров (рис. 2.3.).
Нормальные товары это – 1) необходимые блага, спрос на которые растет медленнее чем доход; 2) предметы роскоши, спрос на которые растет быстрее дохода.
Функция полезности означает соотношение объемов потребляемых товаров и уровня полезности потребителя.
В практике наиболее часто используется следующие четыре типа функций полезности:
1. Функция с полным взаимозамещением благ
,
где Y1, Y2 – потребляемые блага,
b1, b2 – константа.
2. Неоклассическая функция полезности
где 
.
3. Функция с полным взаимодополнением благ
,
4. Функция смешанного замещающе – дополняющего типа
,
где u1, u2 – функции; b1, b2, c1, c2 – константа.
III. Лабораторное задание
1. С помощью компьютера выполнить тестовый опрос. Директория MICRO\LABWORK2\var x.bat.
2. Используя данные полученного варианта, выполнить задание по следующему плану:
2.1. Определить тип функции.
2.2. Построить график функции.
2.3. Используя программу из директории MICRO\POTREB\program.exe, построить карту кривых безразличия (три линии).
3. Перечислить свойства кривых безразличия.
IV. Содержание отчета
Отчет по лабораторной работе составляется каждым студентом.
Отчет должен содержать следующие результаты и выводы:
1. Тему и вариант работы.
2. Цель работы.
3. Аналитическое и графическое решение задачи.
4. Количество баллов, набранных при тестовом опросе.
V. Варианты к лабораторной работе
1. U = 4 . Y1 + 2 . Y2.
2. U = min (Y1/5, Y2/3).
3. U = 3 . Y1 + 4 . Y2.
4. U = min (Y1/5, Y2/4).
5. U = 2 . Y1 + 2 . Y2.
6. U = min (Y1/5, Y2/2).
7. U = 4 . Y1 + 4 . Y2.
8. U = min (Y1/4, Y2/3).
9. U = 4 . Y1 + 3 . Y2.
10. U = min (Y1/4, Y2/2).
11. U = 4 . Y1 + 2 . Y2.
12. U = min (Y1/3, Y2/4).
13. U = 3 . Y1 + 2 . Y2.
14. U = min (Y1/4, Y2/5).
15. U = 3 . Y1 + 3 . Y2.
Лабораторная работа №3
Производство и издержки. Иллюстрация процесса производства с помощью функции Кобба– Дугласа
I. Цель работы
1. Исследование издержек производства.
2. Построение графиков изоквант и изокост.
II. Общие сведения
Производственная деятельность – это процесс получения единицы продукции при определенной комбинации ресурсов (L, K) и данном уровне технологии.Это можно записать с помощью производственной функции
Y=F (x1, x2),
где x1,x2 – ресурсы. Размерность 2 выбрана для удобства построения графиков.
Производственная функция характеризует зависимость между максимально возможным объемом выпуска (Q) и количеством применяемых ресурсов, например труда (L) и капитала (K). Так же как и для функции полезности и кривых безразличия, можно выделить, по крайней мере, 4 типа производственных функций:
1. Функция с полным взаимозамещением ресурсов
, a1>0,a2>0.
2. Неоклассическая функция: 
,
где 
, 
>0, 
.
3. Функция с полным взаимодополнением ресурсов:
.
4. Функция смешанного замещающе-дополняющего типа:
.
В теории производства традиционно используется двухфакторная производственная функция Кобба-Дугласа:
где П – объем продукции,
L – количество труда,
K – объем капитала,
A – коэффициент пропорциональности,
- коэффициенты эластичности факторов производства.
Графически производственная функция - это линия равного выпуска-изокванта, подобная кривой безразличия. Если кривая безразличия характеризует один и тот же уровень полезности различных комбинаций потребительских благ, то изокванта – альтернативный вариант комбинаций факторов производства (например L и К) при определенном выпуске продукции. Таким образом, на карте выпуска каждая изокванта представляет множество комбинаций производственных ресурсов или технически эффективных способов производства определенного объема продукции. В отличие от кривых безразличия каждая изокванта характеризует определенный объем выпуска.
Функция издержек – изокоста – показывает те затраты на покупку факторов производства, которые может позволить себе фирма. Если цены факторов производства будут меняться, то изокоста меняет свой наклон.
Определение оптимального объема производства при минимальных издержках предполагает точку касания производственной функции и функции издержек. Используя краткосрочную производственную функцию неоклассического типа, можно изобразить изокванты и изокосты, а также графики средних и предельных затрат, проиллюстрировать таким образом основы теории производства.
III. Лабораторное задание
1. С помощью компьютера выполнить тестовый опрос. Директория MICRO\LABWORK3\var x.bat.
2. Решить задачу, используя данные полученного варианта, по нижеследующему плану:
1. Используя производственную функцию Кобба-Дугласа: 
, построить карту изоквант для заданного выпуска продукции y=… по варианту (оси координат х1 и х2).
2. Используя функцию издержек 
, по формуле 
построить изокосты: прямые линии с углом наклона 
, где 
и 
- цены факторов производства 
и 
.
3. Определить точки касания изокост и изоквант
;
;
;
;
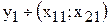в которых минимизируются издержки для каждого выпуска.
4. Используя функцию издержек 
(по варианту), заполнить таблицу общих издержек
| Y | x1 | x2 | C |
и построить график 
.
Для демонстрации процесса построения можно использовать программу из директории C:\MICRO\WORK, запуск осуществляется lab1.exe.
IV. Содержание отчета
Отчет по лабораторной работе составляется каждым студентом.
Отчет должен содержать следующие результаты и выводы:
1. Тему и вариант работы.
2. Цель работы.
3. Результаты выполнения лабораторной работы.
4. Раскрытое содержание всех видов издержек и запись формул.
5. Графическое решение задачи.
6. Выводы по работе.
V. Варианты к лабораторной работе
1. Y=1; 3; 5; 7; С=6 . X1+4 . X2+2.
2. Y=1; 2; 3; 4; С=6 . X1+4 . X2+4.
3. Y=2; 4; 6; 8; С=6 . X1+4 . X2+6.
4. Y=3; 5; 7; 9; С=3 . X1+2 . X2+2.
5. Y=2; 3; 4; 5; С=3 . X1+2 . X2+4.
6. Y=1; 3; 5; 7; С=4 . X1+3 . X2+6.
7. Y=1; 2; 3; 4; С=4 . X1+3 . X2+2.
8. Y=2; 4; 6; 8; С=4 . X1+3 . X2+4.
9. Y=3; 5; 7; 9; С=4 . X1+3 . X2+6.
10. Y=2; 3; 4; 5; С=8 . X1+6 . X2+2.
11. Y=1; 3; 5; 7; С=8 . X1+6 . X2+4.
12. Y=1; 2; 3; 4; С=8 . X1+6 . X2+6.
13. Y=2; 4; 6; 8; С=2 . X1+3 . X2+2.
14. Y=3; 5; 7; 9; С=2 . X1+3 . X2+4.
15. Y=2; 3; 4; 5; С=2 . X1+3 . X2+6.
Лабораторная работа №4
