Примерные решения практических заданий
1. На плоскости относительно прямоугольной системы координат дано каноническое уравнение эллипса с параметрами a, b. Перевести аффинным преобразованием данный эллипсв единичную окружность с центром в начале координат.
Решение.
Каноническое уравнение эллипса 
.
Перепишем его в виде 
.
Рассмотрим аффинное преобразование 
.
Оно переводит эллипс в единичную окружность с уравнением 
.
Штрихи над координатами x и y показывают, что единичная окружность является образом. После того как уравнение образа получено, то штрихи можно не писать.
2. На плоскости относительно прямоугольной системы координат даны две единичные окружности: с центром в начале координат и с центром в точке 
.Перевести одну окружность в другую аффинным преобразованием.
Решение.
Рассмотрим две единичные окружности
и 
.
Рассмотрим движение 
. Оно является параллельным переносом на вектор с координатами 
и переводит первую окружность во вторую.
3. Можно ли перевести любой эллипс в любой эллипс движением плоскости и почему?
Решение.
Из задач 1, 2 вытекает, что аффинным преобразованием можно перевести любой эллипс в любой эллипс. Для этого надо перевести оба эллипса в единичные окружности с теми же центрами, а затем перевести окружности друг в друга. Однако в случае произвольных канонических параметров эллипсов этого нельзя добиться движением, так как параметры отвечают за размеры эллипсов.
4. Можно ли перевести эллипс в гиперболу (или любую другую кривую 2 порядка) аффинным преобразованием и почему?
Решение.
Невозможно перевести аффинным преобразованием эллипс в гиперболу, так как эти фигуры имеют различные инвариантные свойства. В частности, эллипс является ограниченной фигурой, а гипербола – неограниченной. Эллипс не имеет асимптот, а гипербола имеет.
Аналогичные задачи надо уметь решать для всех кривых 2 порядка на плоскости.
Сделать следующие выводы.
Любой эллипс можно перевести в любой эллипс аффинным преобразованием.
Два эллипса можно перевести друг в друга движением плоскости только если они имеют одинаковые канонические параметры.
Сделать аналогичные выводы для других кривых 2 порядка на плоскости.
Составить список инвариантных (относительно аффинных преобразований) свойств и показать, что кривые из разных канонических классов имеют разные инвариантные свойства. Следовательно, не могут быть переведены друг в друга аффинным преобразованием.
Записать аффинное уравнение кривой 2 порядка в проективных однородных координатах и, наоборот, записать однородное уравнение кривой 2 порядка в аффинных координатах.
Решение для гиперболы.
Рассмотрим каноническое уравнение гиперболы на аффинной плоскости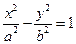 
, где 
- координаты точек плоскости относительно аффинной системы координат O e 1 e 2.
Пополним плоскость несобственными точками и на пополненной плоскости рассмотрим проективную однородную систему координат R={E1,E2,E3,E}, где O = E3, а точки E1, E2 порождаются векторами e 1, e 2.
Формулы связи между аффинными и проективными однородными координатами 
. Подставим 
в уравнение гиперболы:
.
Умножив уравнение на 
, получим
Это уравнение гиперболы на пополненной плоскости в однородных координатах.
Аналогично можно получить уравнения других девяти кривых в однородных координатах на пополненной плоскости
