Тема 1. Кинематика поступательного и вращательного механического движения
Цель занятия: Обобщить и закрепить имеющиеся у студентов знания по теме «Кинематика поступательного и вращательного механического движения»
Задачи занятия:
- проконтролировать уровень усвоения студентамиосновных понятийи закономерностей по рассматриваемой теме;
- сформировать умения применять полученные теоретические знания для решения задач на расчет кинематических параметров поступательного и вращательного движения;
-сформировать умения составлять таблицы при систематизации и обобщении знаний на примере основных уравнений кинематики поступательного и вращательного движения;
-формировать умения выделять признаки сходства в описании изучаемых движений.
Требования к исходному уровню знаний:
Знать определения следующих физических понятий:
· Физика как наука;
· Основные и дополнительные единицы СИ
· Механика, как раздел физики;
· Кинематика, как раздел механики;
· Механическое движение;
· Разложение вектора на составляющие;
· Материальная точка;
· Абсолютно твердое тело
· Система отсчета;
· Радиус – вектор;
· Степень свободы: определение, количество степеней свободы при различных видах движения
· Кинематические уравнения движения точки;
· Траектория;
· Длина пути;
· Перемещение;
· Поступательное движение;
· Вращательное движение.
Знать определение, уметь записать формулы, которыми они определяются, указать единицы измерения и направление (для векторных) следующих физических величин:
· Скорость;
· Средняя скорость;
· Мгновенная скорость;
· Средняя путевая скорость;
· Ускорение;
· Среднее ускорение;
· Ускорение;
· Мгновенное ускорение;
· Тангенциальное ускорение;
· Нормальное ускорение;
· Средняя угловая скорость;
· Мгновенная угловая скорость;
· Угловое ускорение;
· Период вращения;
· Частота вращения.
Уметь записать основные уравнения кинематики для равноускоренного поступательного и вращательного движения.
Уметь записать формулы, связывающие кинематические величины, характеризующие поступательное и вращательное
Сведения из теории
Положение материальной точки в пространстве задается радиус-вектором 
:
,
где 
, – единичные векторы направлений (орты); x, y, z – координаты точки.
Кинематические уравнения движения (в координатной форме)
x= f 1 (t); y = f 2 (t); z = f 3 (t),
где t – время.
Средняя скорость движения
,
где 
– перемещение материальной точки в интервале времени 
.
Средняя путевая скорость
,
где D s – путь, пройденный точкой за интервал времени D t.
Мгновенная скорость
,
где 
– проекции скорости 
на оси координат.
Абсолютная величина скорости
.
Ускорение
,
где 
– проекции ускорения 
на оси координат.
Абсолютная величина ускорения
.
При произвольном (криволинейном движении ускорение можно представить как сумму нормального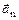 
и тангенциального 
ускорений
.
Абсолютная величина этих ускорений
,
где R – радиус кривизны в данной точке траектории.
Классификация движения, в соответствии с параметрами aτ и an:
1) aτ = 0, an = 0 — прямолинейное равномерное движение;
2) aτ = а = const, ап = 0 — прямолинейное равнопеременное движение.
При таком виде движения
.
Если начальный момент времени t1 = 0, а начальная скорость v1 = v0, то, приняв t2 = t и v2 = v, получим 
, откуда v = v0 + at.
Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, найдем, что длина пути, пройденного точкой, в случае равнопеременного движения
3) aτ = f(t), ап = 0 — прямолинейное движение с переменным ускорением;
4) aτ = 0, ап = const. При aτ = 0 скорость изменяется только по направлению. Из формулы 
следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным;
5) aτ = 0, ап ≠ 0 — равномерное криволинейное движение;
6) aτ = const, ап ≠ 0 — криволинейное равнопеременное движение;
7) aτ = f(t), ап ≠ 0 — криволинейное движение с переменным ускорением.
Кинематические уравнения движения материальной точки вдоль оси х:
а) при равномерном движении –
х = х 0 + vt, v = const, a x = 0;
б) при равнопеременном движении –
.
При вращательном движении положение твердого тела определяется углом поворота (угловым перемещением) j. Кинематическое уравнение вращательного движения в общем виде
j = f (t).
Средняя угловая скорость
где Dj – изменение угла поворота за интервал времени D t.
Мгновенная угловая скорость
Угловое ускорение
.
Кинематическое уравнение вращения тела:
а) при равномерном вращении (w = const, e = 0) –
,
где jо – начальное угловое перемещение; t – время.
б) при равнопеременном вращении (e = const) –
где w0 – начальная угловая скорость; t – время.
в) частота вращения
n = N / t или n = 1 / T
где N – число оборотов, совершаемых телом за время t; Т – период вращения (время одного полного оборота).
Связь между линейными и угловыми величинами, характеризующими движение материальной точки, принадлежащей вращающемуся телу:
а) длина пути, пройденного точкой по дуге окружности радиусом R при повороте тела на угол j,
;
б) линейная скорость точки
;
в) тангенциальное ускорение точки
;
г) нормальное ускорение точки
.
Задания для практической части занятия.
1. Тело брошено со скоростью v0=15 м/c под углом α=300 к горизонту. Пренебрегая сопротивлением воздуха, определите: 1) высоту подъема тела; 2) дальность полета (по горизонтали) тела; 3) время его движения.
Ответ: 1) 2,87 м; 2) 19,9м; 3) 1,53с.
2. Тело брошено под углом α к горизонту. Пренебрегая сопротивлением воздуха, определите этот угол, если максимальная высота подъема меньше дальности полета в 4,5 раза.
Ответ: α=41,60
3. Тело брошено со скоростью v0=20 м/c под углом α=300 к горизонту. Пренебрегая сопротивлением воздуха, определите для момента времени t=1,5 с после начала движения: 1) нормальное ускорение; 2)тангенциальное ускорение.
Ответ: 1) аτ=2,58 м/с2; 2) аn=9,47 м/с2.
4. Тело брошено горизонтально со скоростью v0=15 м/c. Пренебрегая сопротивлением воздуха, определить радиус кривизны траектории тела через t=2 с после начала движения.
Ответ: R=102м
5. Зависимость пройденного пути от времени задается уравнением
s=A-Bt+Ct2+Dt3 (А= 6м; В= 3м/с; С= 2 м/с2 ;D= 1м/с3). Определите для тела в интервале времени от t1 =1 до t2 =4 с: 1) среднюю скорость; 2) среднее ускорение.
Ответ:1) vср=28 м/с; 2) аср=19 м/с2.
6. Зависимость пройденного пути от времени задается уравнением
s=A-Bt+Ct2+Dt3 (А= 6м; В= 3м/с; С= 0,2 м/с2 ;D= 1м/с3). Определите, через сколько времени после начала движения ускорение а тела станет равным
2,8 м/с2.
Ответ:t=4с.
7. Нормальное ускорение точки, движущейся по окружности радиусом R= 4м, задается уравнением аn= A+Bt+Ct 2 (А= 1 м/с2 ;В= 6 м/с3; С= 9 м/с4). Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время t1=5с после начала движения; 3) полное ускорение для момента времени t2=1с
Ответ: 1) аτ=6 м/с2; 2) S1=85м; 3) а2=6 м/с2.
8. Материальная точка движется вдоль прямой так, что её ускорение линейно растет и за первые 10 с достигает значения 5 м/с2. Определите в конце десятой секунды: 1) скорость точки; 2) пройденный точкой путь.
Ответ: 1) v1=25 м/с; 2) S1=83,3м.
9. Якорь электродвигателя, имеющий частоту вращения n=50 с-1, после выключения тока, сделав N= 628 оборотов, остановился. Определить угловое ускорение e якоря.
Ответ:e = 12,5 рад/с2;
10. Колесо автомашины вращается равнозамедленно. За время t=2 мин оно изменило частоту вращения от 240 до 60 мин -1. Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
Ответ:e = 12,5 рад/с2; 2) N =300
11. Точка движется по окружности радиусом R=15м с постоянным тангенциальным ускорением аτ.. К концу четвертого оборота после начала движения линейная скорость точки v1=15 см/с. Определите нормальное ускорение точки через t2 =16 с после начала движения.
Ответ: аn=1,5 см/с2.
12. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 
(А=0,5 рад/с2). Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2)угловое ускорение диска;3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное, нормальное и полное ускорение.
Ответ: 
=2 рад/с; 2) e = 12,5 рад/с2;
3) аτ=0,8 м/с2; 2) аn=3,2 м/с2; а=3,3 м/с2
