МеТОДИЧЕСКИЕ УКАЗАНИЯ
К лабораторным и практическим работам
по дисциплине ОП.08 «Теория алгоритмов»
специальность 09.02.03 Программирование в компьютерных системах
2 курс
2016г.
Указания к лабораторным и практическим работам разработаны на основе Федерального государственного образовательного стандарта среднего профессионального образования по специальности 09.02.03 Программирование в компьютерных системах и рабочей программы по дисциплине
Организация-разработчик: Государственное бюджетное профессиональное образовательное учреждение Республики Крым «Феодосийский политехнический техникум»
Разработчик:
Монастырная Е.А., преподаватель специальных дисциплин
Методические указания рассмотрены и одобрены на заседании цикловой комиссии компьютерных дисциплин.
Протокол № _ от «_» 09 2016 года
Председатель цикловой комиссии ________________________ Дворянова Т.Н.
© Монастырная Е.А.
СОДЕРЖАНИЕ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.. 4
Инстркуция по охране труда и технике безопасности. 6
Лабораторная работа № 1. 8
лабораторная работа №2. 14
лабораторная работа № 3. 20
Лабораторная работа №4. 24
Лабораторная работа №5. 28
Практическая работа №1. 35
Практическая работа №2. 42
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
В соответствии с учебным планом подготовки специалистов предполагается выполнение обучающимися лабораторных и практических работ с целью
- обобщения, систематизации, углубления, закрепления полученных теоретических знаний по дисциплине
- формирования умений применять полученные знания на практике, реализации единства интеллектуальной и практической деятельности;
- развития интеллектуальных умений у будущих специалистов: аналитических, проектировочных, конструктивных и других;
- выработки при решении поставленных задач таких профессионально значимых качеств, как самостоятельность, ответственность, точность, творческая инициатива.
По каждой работе оформляется отчет. Все отчеты собираются в одну папку-журнал. Каждая работа должна быть выполнена и защищена.
Студенты, не выполнившие и не защитившие работы, к сдаче экзамена не допускаются.
Согласно учебного плана специальности 09.02.03 Программирование в компьютерных системах по дисциплине ОП.08 Теория алгоритмов объем лабораторных/практических работ предусматривается в количестве 26 часов.
В результате выполнения лабораторных и практических обучающийся приобретает умения:
У.1 разрабатывать алгоритмы для конкретных задач;
У.2 определять сложность работы алгоритмов.
Что позволяет сформировать у обучающегося профессиональные и общие компетенции:
ПК 1.1 Выполнять разработку спецификаций отдельных компонент.
ПК 1.2 Осуществлять разработку кода программного продукта на основе готовых спецификаций на уровне модуля.
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.
ОК 4. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии для совершенствования профессиональной деятельности.
ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями.
ОК 7. Ставить цели, мотивировать деятельность подчиненных, организовывать и контролировать их работу с принятием на себя ответственности за результат выполнения заданий.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9. Быть готовым к смене технологий в профессиональной деятельности.
Таблица 1.
| № п/п | Название работы | Формируемые компетенции | Количество часов |
| Пз 1 Способы записи алгоритмов | ПК 1.1, ПК 1.2 | ||
| Лр 1 Составление простого алгоритма | ПК 1.1, ПК 1.2 | ||
| Лр.2 Составление разветвленного алгоритма | ПК 1.1, ПК 1.2 | ||
| Лр.3. Решение системы уравнений | ПК 1.1, ПК 1.2 | ||
| Лр.4. Составление циклического алгоритма | ПК 1.1, ПК 1.2 | ||
| Лр.5. Табуляция функции | ПК 1.1, ПК 1.2 | ||
| Пз. 2. Использование одномерных массивов | ПК 1.1, ПК 1.2 |
Инстркуция по охране труда и технике безопасности
при проведении лабораторных и практических работ за компьютером
в лаборатории Технологии разработки БД
Иот-057 2014
Общие положения
Студенты должны выполнять требования по технике безопасности, охране труда, пожарной безопасности, установленные для лаборатории.
Перед началом работы
Студент может быть допущен к выполнению работы только после инструктажа по технике безопасности.
Студенты могут включать или выключать компьютер только с разрешения преподавателя.
Перед началом работы, студент должен осмотреть компьютер и при обнаружении неисправности или подозрительных явлений, сообщить об этом преподавателю.
На рабочем столе студента не должно быть посторонних предметов.
Во время работы
Студент должен соблюдать требования к организации работы за компьютером.
Правильно сидеть за компьютером (таблицы 1 и 2);
Таблица 1-Как сидеть за компьютером
| № п/п | Часть тела | Расположение |
| Ступни ног | На полу или на подставке для ног | |
| Бёдра | Горизонтально | |
| Плечо | Вертикально | |
| Локти | Под углом 70-90о к вертикали | |
| Запястья | Под углом не более 15-20о к горизонтали | |
| Голова | Наклон 15-20о от вертикали |
Рабочее место с компьютером желательно оснащать пюпитром (держателем) для документов, который должен быть подвижным и устанавливаться вертикально (или с наклоном) на том же уровне и расстоянии от глаз, что и монитор (см. Таблицу 2).
Таблица 2–Расстояние от монитора до глаз
| № п/п | Размер монитора (диагональ) | Расстояние, см |
| 14-15" (35-38 см) | 60-70 | |
| 17" (43 см) | 70-80 | |
| 19" (48 см) | 80-90 | |
| 21" (53 см) | 90-100 |
Соблюдать режим работы за компьютером
Позволяется вариант организации занятий, при котором предусматривается часть академических часов – в виде теоретических занятий, другая часть часов – в виде практических занятий.
Для того, чтобы во время практических занятий работа за компьютером не ухудшала здоровье, нужно соблюдать правильный режим труда и отдыха, рекомендации относительно которого приведены ниже (см. Таблицу 3).
Таблица 3–Режим труда и отдыха
| Категор работы | Характер работы | Режим труда и отдыха |
| Разработка программ | Выполняют работу преимущественно с монитором и документацией при необходимости интенсивного обмена информацией с компьютером и высокой частотой принятия решений. Работа характеризуется интенсивным умственным творческим трудом с повышенным напряжением зрения, концентрацией внимания на фоне нервно-эмоционального напряжения, вынужденной рабочей позой, общей гиподинамией, периодической нагрузкой на кисти верхних конечностей. Работа выполняется в режиме диалога с компьютером в свободном темпе с периодическим поиском ошибок в условиях дефицита времени. | Следует назначать регламентированный перерыв для отдыха продолжительностью 15 минут через каждый час работы за монитором. |
| В качестве оператора | Выполняют работу, связанную с учётом информации, полученной с монитора по предварительному запросу, или поступающей с него. Работа сопровождается перерывами разной продолжительности, связана с выполнением другой работы и характеризуется как работа с напряжением зрения, небольшими физическими усилиями, нервным напряжением средней степени и выполняется в свободном темпе. | Следует назначать регламентированные перерывы для отдыха продолжительностью 15 минут через каждые два часа работы. |
| Компьютерный набор | Выполняет однообразные по характеру работы с документацией и клавиатурой и нечастыми непродолжительными переключениями взгляда на экран дисплея, с вводом данных с высокой скоростью. Работа характеризуется как физический труд с повышенной нагрузкой на кисти верхних конечностей на фоне общей гиподинамии с напряжением зрения (фиксация зрения преимущественно на документах), нервно-эмоциональным напряжением. | Следует назначать регламентированные перерывы для отдыха продолжительностью 10 минут после каждого часа работы за монитором. |
Занятия прекращаются немедленно в случае возникновения пожара в лаборатории или учебном корпусе, получении предупреждения о возможности стихийного бедствия, понижении температуры в лаборатории ниже 18 градусов.
Если произошел несчастный случай с преподавателем или студентом, по–возможности, оказать помощь и сообщить директору о происшедшем.
По окончании работы
Студенты должны убрать свои рабочие места.
Зав. лабораторией Дворянова Т.Н.
"Согласовано"
Зам.директора по УР Сердюкова О.Г.
Инженер по ОТ Гаспарян Н.В.
Председатель профкома Берладин Ю.Е.
Лабораторная работа № 1
Тема: Построение линейного алгоритма.
Цель: Научится составлять блок-схемы линейного алгоритма.
Оборудование: ПК.
Ход работы.
- Повторить теоретическую часть.
- Выполнить практическое задание.
- Ответить на контрольные вопросы.
Теоретический материал
Алгоритмом называется точное предписание, определяющее последовательность действий исполнителя, направленных на решение поставленной задачи. В роли исполнителей алгоритмов могут выступать люди, роботы, компьютеры.
Понятие алгоритма в программировании является фундаментальным. Для алгоритма важен не только набор определенных действий, но и то, как они организованы, т.е. в каком порядке они выполняются.
Свойства алгоритма:
- понятность – все действия должны входить в систему команд исполнителя, т.е. быть понятны ему;
- дискретность - алгоритм делится на отдельные элементарные шаги;
- определенность - каждая команда однозначно определяет действие исполнителя;
- конечность(результативность) - алгоритм должен завершаться за конечное число шагов.
- массовость – алгоритм позволяет решать целый класс похожих задач.
Графический способ (в виде б лок-схемы)
Блок схема – это графическое представление алгоритма при помощи стандартных обозначений. Блок схемы составляются в соответствии с ГОСТами. ГОСТы алгоритмов: ГОСТ 19.002-80, ГОСТ 19.003-80. На схемах алгоритмов выполняемые действия изображаются в виде отдельных блоков, которые соединяются между собой линиями связи в порядке выполнения действий. На линиях связи могут ставиться стрелки, причем, если направление связи слева направо или сверху вниз, то стрелки не ставятся. Блоки нумеруются. Внутри блока дается информация о выполняемых действиях.
Таблица 1 – Основные блоки, используемые при составлении алгоритмов
| Название | Обозначение | Назначение |
| Пуск, Останов | 
| Начало-конец алгоритма |
| Процесс | 
| Любое вычислительное действие |
| Решение | 
| Проверка условия |
| Ввод-вывод | 
| Ввод-вывод данных |
| Соединитель | 
| Используется на линиях разрыва |
| Комментарий | 
| Комментарий |
Линейные алгоритмы
Линейный алгоритм – алгоритм, в котором все команды выполняются последовательно друг за другом.
Приведем пример решения:
Постановка задачи
Цель. Вычислить периметр и площадь прямоугольного треугольника, если заданы длины двух его катетов
Входные данные
а – длина одного катета.
b– длина другого катета
Выходные данные.
P – периметр треугольника, S – площадь треугольника.
Т.к. для вычисления периметра нужна длина третьей стороны, то к выходным данным следует отнести и ее.
с– третья сторона.
Математическая модель.
Вычислим длину третьей стороны: с= 
определим периметр: Р= а+ b+ с
Вычислим площадь: S= а* b/2
Алгоритм решения
 |
|
Практическое задание
1 Ответить на контрольные вопросы
2. Выполнить описание решения задания.
3. Составить блок-схему алгоритма, согласно варианту задания.
Варианты заданий:
1. Вычислите длину окружности, площадь круга и объём шара одного и того же заданного радиуса r.
2. Вычислите площадь кольца, если заданы радиусы окружностей.
3. Вычислить значение выражения y =.Sin  , где a =
, где a =  , b= (2+
, b= (2+  )5 .
)5 .
4. Вычислите площадь и периметр треугольника по трем его сторонам a, b, c..
5. Идет k секунд суток. Определите, сколько полных часов (h), минут (m) прошло к этому моменту.
6. Жидкость в объеме v1 и температурой t1 смешали с жидкостью v2 и температурой t2. Найти объем смеси и температуру.
Контрольные вопросы.
1. Дайте определение алгоритма.
2. Назовите способы задания алгоритмов.
3. Назовите этапы построения линейного алгоритма.
4. Назовите основные свойства алгоритма.
Содержание отчета
1Тема. Цель
2 Ответы на контрольные вопросы
3 выполненное практическое задание
Лабораторная работа №2
Тема: Составление разветвленного алгоритма
Цель работы: Научиться составлять алгоритмы разветвляющейся структуры, учитывая условия различной сложности.
Оборудование: ПК
Ход работы.
1. Повторить теоретическую часть.
2. Выполнить практическое задание.
3. Ответить на контрольные вопросы.
Теоретическая часть
При составлении схем алгоритмов часто возникает необходимость проведения анализа исходных данных или промежуточных результатов вычислений и определения дальнейшего порядка выполнения вычислительного процесса в зависимости от результатов этого анализа. Алгоритмы, в которых в зависимости от выполнения некоторого логического условия происходит разветвление вычислений по одному из нескольких возможных направлений, называют разветвляющимися. Подобные алгоритмы предусматривают выбор одного из альтернативных путей продолжения вычислений. Каждое возможное направление вычислений называется ветвью. Логическое условие называют простым, если разветвляющийся процесс имеет две ветви, и сложным, если процесс разветвляется на три и более ветви.
Любое сложное логическое условие может быть представлено в виде простых.
Рассмотрим пример разветвляющегося алгоритма с простым логическим условием.
 Пример 1.2. Даны два числа а и b.
Пример 1.2. Даны два числа а и b.
Найти
Очевидно, что для определениия ветви, по которому необходимо производить процесс вычисления значения х, достаточно проверить выполнение одного из условий, например а>b. Если условие а>b не выполняется, то очевидно и без дополнительной проверки, что будет выполнено условие а < b. Следовательно, вариант схемы алгоритма будет выглядеть следующим образом (рис 1.3).

Рис 1.3. Схема простого разветвляющегося алгоритма
Рассмотрим примеры алгоритмов разветвляющейся структуры в случаях необходимости анализа более сложных логических условий.
a / b, если а > 0
Пример 1.3. Даны два числа а и b. Найти х = - а - b, если а = 0.
а + b, если а < 0
Из условия очевидно, что предполагаемый вычислительный процесс должен предусматривать выбор одного из альтернативных путей вычислений в зависимости от значения переменной а.
При этом алгоритм может быть представлен в одном из двух вариантов: с разветвлением по сложному логическому условию (рис 1.4 а) и с разветвлением при разложении сложного логического условия на простые (рис. 1.46).
Пример 1.4. Вычислить значение Y при заданных значениях а, х.


Рис 1.4, Схемы алгоритмов разветвляющейся структуры: а) - со сложным логическим условием; б) - при разложении сложного логического условия на простые
Разветвляющимся называется алгоритм, в основе которого лежит одна из структур "ветвления"
Условие, от которого зависит выбор пути решения, представляет собой логическое выражение. Самое простое – переменная логического типа. Наиболее часто встречающееся – два арифметических выражения, соединенные знаком отношения.
Отличия явных и неявных условий
Явные условия задаются непосредственно в условии задачи. Неявные появляются в процессе анализа задачи и служат для обработки исключительных ситуаций.
Правила записи составных условий
условия могут быть сложными, те содержать несколько логических выражений. Каждая часть условия заключается в скобки.
Варианты заданий:
1. Вычислить значение функции, где a, b, x – любое
 
| 2. Вычислить значение функции, где x, b - любое
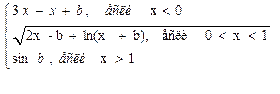
|
3. Вычислить значение функции, где a, x - любое

| 4. Вычислить значение функции, где x, b - любое

|
5. Вычислить значение функции, где x,a - любое

| 6. Вычислить значение функции, где a, t - любое

|
Примеры алгоритмов с многозначным ветвлением.
Обычно, если необходимо проверить достаточно много условий, использующих отношение типа "=" и в зависимости от них выполнять те или иные действия используют алгоритм с многозначным ветвлением.
Правила составления разветвляющихся алгоритмов с использованием выбора
Правила составления рассмотрим на примере.
Задача. Вывести название дня недели по его порядковому номеру.
1 Формализация.
1.1 Постановка задачи.
Цель. Вывести на экран название дня недели в зависимости от его порядкового номера.
Входные данные.
n – номер дня недели. Т.к. номер дня недели может принимать значения от 1 до 7, то можно для описания этой переменной создать интервальный тип, а можно воспользоваться стандартным типом byte.
Выходные данные.
Т.к. при решении этой задачи не требуется выполнение ни каких вычислений, то выходной величиной будет строковая константа, значение которой– название дня недели.
1.2 Модель
ввод значения n
n=1;"понедельник"
n=2;"вторник"
n=3;"среда"
n=4;"четверг"
n=5;"пятница"
n=6;"суббота"
n=7;"воскресенье"
иначе "неделя кончилась"
Алгоритм решения
 |
 1
1




 2 +
2 +
 |



 3 +
3 +


 +
+

 4
4




 +
+
 5
5



 +
+


 6
6

 7 +
7 +


 +
+


 8
8
 |
 9
9
 |
Алгоритм выполняется следующим образом.
Шаг 1. Вводится номер дня недели, это и будет значением селектора.
Шаг 2.- 8. Значение селектора сравнивается по очереди с каждым из номеров дней недели и как только значение совпадет, будет выведено сообщение с названием дня недели.
Шаг 9. Этот шаг выполняется в случае ввода несуществующего дня недели, выдается соответствующее сообщение.
3. Задания
По номеру в журнале выберите индивидуальное задание из нижеприведенного списка. В качестве f(x) использовать по выбору: sin(x), х2; е  . Отредактируйте вид формы и текст программы, в соответствии с полученным заданием.
. Отредактируйте вид формы и текст программы, в соответствии с полученным заданием.
1. a= 
2. 
3. 
4. 
5. 
6.  7
7
7. 
8. 
9. 
10. 
11.  .
.
12.  .
.
13.  .
.
1. По номеру n (n>0) некоторого года определить с - номер его столетия (учесть, что, к примеру, началом XX столетия был 1901, а не 1900 год).
2. Для целого числа  от 1 до 99 вывести фразу “мне
от 1 до 99 вывести фразу “мне  лет”, учитывая при этом, что при некоторых значениях
лет”, учитывая при этом, что при некоторых значениях  слово “лет” надо заменить на слово “год” или “года”.
слово “лет” надо заменить на слово “год” или “года”.
3. Для натурального числа  вывести фразу “мы выпили
вывести фразу “мы выпили  бутылок пива”, согласовав слово “бутылка” с числом
бутылок пива”, согласовав слово “бутылка” с числом  .1 Вводится число от 1 до 4, определяющее пору года. Дать название этой поры года (1 — зима, 2 — весна, 3 — лето, 4 — осень).
.1 Вводится число от 1 до 4, определяющее пору года. Дать название этой поры года (1 — зима, 2 — весна, 3 — лето, 4 — осень).
4. Вводится число от 1 до 7, определяющее день недели. Дать название этого дня (1 — понедельник, 2 — вторник,..., 7 — воскресенье).
5. Вводятся числа 12, 1, 2, определяющие зимний месяц года. Дать название этого месяца года (1 — январь, 2 — февраль, 12 — декабрь).
6 Вводится значение года в укороченной форме (от 0 по 10). Вывести значение года текущего столетия в полном формате (0 – 2000, 1 – 2001 и т.д.).
7 Вводится номер месяца (1, 2, …, 12). Вывести количество дней в указанном месяце.
8 Написать программу, которая запрашивает у пользователя номер дня недели и выводит одно из сообщений: «Рабочий день», «Суббота», «Воскресенье».
9 Вводится число от – 10 до 10. Вывести сообщение: введенное число больше 0, меньше 0 или равно 0.
10 Вводится число от 2 до 10. Вывести сообщение: четное или нечетное введенное число.
11 Вводится число от 1 до 10. Дать название этого числа (1 — один, 2 — два,..., 10 — десять).
12 Вводятся числа 3, 4, 5, определяющие весенний месяц года. Дать название этого месяца года (3 — март, 4 — апрель, 5 — май).
13 Определить число дней в месяце. Считать год не високосным
Контрольные вопросы:
1. Какой алгоритм называют алгоритмом с ветвлением?
2. Что такое полный и сокращенный вид алгоритма ветвления?
3. Что используется в качестве условий в ветвлении?
4. Какие знаки отношений можно использовать при составлении условий?
5. Что такое составное условие?
6. Каковы правила записи составных условий?
7. Что такое "селектор" и зачем он нужен?
8. Какого типа должна быть переменная-селектор?
Содержание отчета
1Тема. Цель
2 Ответы на контрольные вопросы
3 выполненное практическое задание
Лабораторная работа №4
Тема: Составление циклического алгоритма.
Цель: Освоить составление алгоритмов для решения задач использующих циклы с параметром.
Ход работы.
1. Изучить теоретический материал.
2. Выполнить практическое задание.
3. Ответить на контрольные вопросы.
4. Составить отчет.
Теоретический материал
Циклом с параметром (со счетчиком) называется алгоритм, в основе которого лежит структура "для"
Такая структура используется для организации циклов с фиксированным, заранее известным числом повторений.
Понятие параметра цикла
Переменная, от которой зависит число повторений тела цикла носит название параметра цикла.
Параметр меняет свое значение от начального к конечному с шагом 1, поэтому его еще называют счетчиком.Тело цикла выполняется до тех пор, пока не будут перебраны все значения параметра цикла.
Переменная-счетчик должна быть порядкового типа- чаще — byte, word, integer, реже — char или одного из пользовательских типов. Использование вещественного типа недопустимо
Начальное и конечное значения параметра цикла могут быть константами, переменными или выражениями и должны принадлежать к одному и том уже типу данных. Начальное и конечное значение нельзя изменять во время выполнения цикла;
Правила организации циклов с параметром рассмотрим на примере.
Дано К чисел. Найти сумму всех чисел до первого отрицательного.
1 Формализация
1.1 Постановка задачи
Цель. Подсчитать сумму чисел среди заданных К чисел. Вычисления закончить, если встретится отрицательное число.
Входные данные.
К – количество чисел. Тк количество чисел – величина целая, то
К: integer.
Х – текущее число. Тк по условию задачи не задано явно какие числа будут суммироваться, то Х: real.
Выходные данные
С – сумма чисел. Тк суммируются числа типа real, то С: real.
1.2 Математическая модель
К ввод количества чисел
С:=0 начальное значение суммы
I:= 1 начальное значение параметра цикла
X ввод текущего числа
X>=0; C:=C+X; I:=K если число положительное, то добавить его к сумме,
иначе присвоить параметру цикла конечное
значение
I:=I+1 новое значение параметра цикла
I>K;C если все числа рассмотрены, печатаем сумму
2 Алгоритм (блок-схема)
 |
- +
 |
3 Псевдокод
Программа ЦиклПарам;
Var
I,K: integer;
X: real;
начало
вывод('количество чисел?'); ввод (К);
С:=0;
Для I:=1 к К делать
начало
вывод ('текущее число?'); ввод (Х);
если Х>= 0 то С:=С+Х иначе I:=К;
конец;
вывод ('сумма чисел до первого отрицательного равна –', С);
конец.
4 Тестирование
Количество чисел 5
С=0
I:=1
текущее число 1
1>= 0 С:=0+1=1
I:= I+1=2
текущее число 5
5>= 0 С:=1+5=6
I:= I+1=3
текущее число -5
-5>= 0 I:= К=5
I:= I+1=6
сумма чисел до первого отрицательного равна– 6
Алгоритм работает правильно
Практическое задание.
Выполнить постановку задачи и математическую модель, составит алгоритм, записав его в виде блок–схемы и псевдокода для решения следующих задач.
1. Найти произведение натуральных чисел на диапазоне [17, 41].
2. Дано К натуральных чисел. Найти сумму чисел, меньших 100.
3. Дано К натуральных чисел. Найти сумму чисел кратных 3.
4. Дано К чисел. Найти произведение четных натуральных чисел.
5. Дано К чисел. Напечатать квадраты всех отрицательных чисел.
6. Дано К чисел. Вывести на экран все числа до первого нуля.
7. Дано К натуральных чисел. Вывести на экран все нечетные числа.
8. Дано К чисел. Вычислить квадратные корни из кратных 4 чисел.
9. Дано К чисел. Вывести на экран все числа до первого отрицательного.
10. Найти сумму квадратов натуральных чисел на диапазоне [1, 21].
11. Дано К чисел. Вывести на экран разность между текущим и предыдущим.
12. Дано К чисел. Найти количество чисел, меньших 10.
13. Дано К чисел. Найти количество нулей.
Контрольные вопросы.
1. Какой циклический процесс называют "циклом с параметром"? Его характерные особенности?
2. Что такое параметр цикла и зачем он нужен?
3. Проанализируйте, чем могут быть выражены значения параметра цикла?
Содержание отчета.
2. Тема, цель.
3. Выполненное практическое задание.
4. Ответы на контрольные вопросы.
Лабораторная работа №5
Тема. Табуляция функции.
Цель. Освоить составление алгоритмов с использованием итерационных циклов для табуляции функции
Ход работы.
- Повторить теоретическую часть.
- Выполнить практическое задание.
- Ответить на контрольные вопросы.
Теоретический материал
Цикл представляет собой последовательность операторов, которая выполняется неоднократно.
Имеется три разновидности цикла — цикл с постусловием ("До"), цикл с предусловием ("Пока") и цикл с параметром ("Для").
Следует знать:
-подавляющее большинство задач с циклами можно решить разными способами, используя при этом любой из трех типов алгоритмов;
-в некоторых случаях все же предпочтительнее использовать какой-то один;
-самым универсальным из всех типов циклов считается цикл с постусловием, поэтому в случае затруднений с выбором можно отдать предпочтение ему;
Цикл с постусловием
повторять
{ тело цикла }
до Условие выхода из цикла;
Вначале выполняется тело цикла — инструкции, которые находятся между повторять и до, затем проверяется значение Условия выхода из цикла. В том случае, если оно равно false (ложь), т. е. не выполняется — инструкции цикла повторяются еще раз. Так продолжается до тех пор, пока условие не станет true (истина).
При выполнении цикла:
– число повторений действий цикла определяется в ходе выполнения алгоритма и во многих случаях заранее неизвестно;
- тело цикла будут выполняться, пока условие выхода из цикла будет оставаться ложным;
- условие — это выражение логического типа: простое выражение отношения или сложное логическое выражение;
- для успешного завершения цикла в его теле обязательно должны быть инструкции, выполнение которых влияет на условие завершения цикла, иначе цикл будет выполняться бесконечно. Другими словами, переменная, которая участвует в условии выхода из цикла, обязательно должна изменяться в теле цикла.
- цикл с постусловием (условие проверяется после выполнения тела цикла), т. е. инструкции тела цикла будут выполнены хотя бы один раз.
-поэтому цикл с постусловием удобно использовать в тех случаях, когда тело цикла гарантированно должно выполниться хотя бы один раз;
Цикл с предусловием состоит из заголовка и тела цикла.
Пока Условие выполнения цикла делать
начало
{ тело цикла }
конец;
Цикл с предусловием аналогичен циклу с постусловием, но проверка Условие выполнения цикла производится в самом начале алгоритма — если значение условия равно true (истина), то выполняются действия тела цикла, находящиеся между начало и конец и снова вычисляется выражение Условие выполнения цикла. Так продолжается до тех пор, пока значение Условие выполнения цикла не станет равно false (ложь).
При выполнении цикла:
* число повторений тела цикла, как правило, заранее неизвестно;
* после слова пока записывается условие продолжения выполнения инструкций цикла;
* условие — это выражение логического типа: простое выражение отношения или сложное выражение отношения (логическое выражение), которое может принимать одно из двух значений: true или false;
* для успешного завершения цикла в его теле обязательно должны присутствовать инструкции, оказывающие влияние на условие выполнения инструкций цикла.
Одна из задач, в которой могут быть использованы цикл постусловием или с предусловием, есть задача табуляции. Под табуляцией следует понимать получение результата для каждого значения аргумента.
Пусть необходимо решить задачу:



|

где х – любое, а принадлежит [-1,3], шаг а = 0,25
Это и есть задача табуляции, когда каждому значению аргумента ставится в соответствие значение функции.
Решение начинается с формализации задачи, которая состоит из двух этапов: постановки задачи и построения модели процесса. Постановка задачи включает выяснение цели задачи, определения и описания(указания типов) входных и выходных данных. По результатам формализации строится алгоритм в виде блок–схемы, затем алгоритм кодируется. Заключительным этапом является проверка правильности работы алгоритма.
Формализация
Постановка задачи
Цель. Вычислить значение функции F по приведенным в условии формулам
Входные данные
а – аргумент.
х– переменная
Так как обе величины могут быть как целыми, так и дробными, то переменные а, х:real.
Выходные данные.
F – Значение функции.
F: real.
Математическая модель.
Отметим решения на числовой прямой
 |

0 1 2
0) Х
1) а=-1
2) После определения вида функции в зависимости от того в какой интервал попадает аргумент, следует выяснить всегда ли функция непрерывна на этом интервале
а < 0; возникают неявные условия, т.к. х может быть любым числом, а возвести в дробную степень можно только неотрицательное число, то должно выполняться условие х≥0;  ; иначе значение F не определено
; иначе значение F не определено
3) 0 < a < 1; возникают неявные условия, тангенс можно вычислить только, если Сos(a2)<>0;F=Cos2(x)+(Sin(a2)/Cos(a2))3 ; иначе значение функции F не определено
1= < a < =2; Функция не задана
4) a > 2; возникают неявные условия, т.к. х может быть любым числом, а извлечь корень можно только из неотрицательного числа и логарифм можно вычислить только для положительных аргументов, то должно выполняться условие х>0; F=  ; иначе значение F не определено.
; иначе значение F не определено.
5) а=а+0,25
6) а>3 – выход из цикла, иначе к п2
Алгоритм решения
Алгоритм выполняется следующим образом.
Шаг 0. Вводится недостающая для вычисления значение переменной х.
Шаг 1 Задается начальное значение аргумента
Дальше н шагах 2, 6, 10, 12 выясняется в какой из интервалов попало значение аргумента
Шаг 2. Если а < 0, то переход к шагу 3 – проверке неявных условий, х≥0. Если условие выполняется, то вычисляется значение функции по формуле  (шаг 4) и выводится результат(шаг 5), иначе выдается сообщение о том, что значение F не определено.
(шаг 4) и выводится результат(шаг 5), иначе выдается сообщение о том, что значение F не определено.
Шаг 6. 0 < a < 1, то переход к шагу 7 – проверке неявных условий Сos(a2)<>0; Если условие выполняется, то вычисляется значение функции по формуле F=Cos2(x)+(Sin(a2)/Cos(a2))3 (шаг 8) и выводится результат(шаг 9), иначе выдается сообщение о том, что значение F не определено.
Шаг 10. Если 1= < a < =2, то выдается сообщение о том. что на этом интервале функция не задана(шаг 11)
Шаг 12. Если a > 2, то переход к шагу 13 – проверке неявных условий х>0. Если условие выполняется, то вычисляется значение функции по формуле; F=  (шаг14); и выводится результат(шаг 15), иначе выдается сообщение о том, что значение F не определено
(шаг14); и выводится результат(шаг 15), иначе выдается сообщение о том, что значение F не определено
Шаг 16. Изменение аргумента на величину шага
Шаг 17. Проверка условия выхода из цикла. Если его значение "ложь", то цикл выполняется еще раз
 |
 0
0
|
 1
1






 2 + -
2 + -
 + -
+ -


|


 3
3

 4
4

 5
5
 |



 6 + -
6 + -
 7 +
7 +


|



 8
8
 |


 9
9
 |
 10 + -
10 + -




 11
11
 |




 12 + -
12 + -




 13 + -
13 + -

|
 |

 15
15
 |

|
 17
17


 - +
- +
 |
Кодирование алгоритма
программа Табуляция;
Var a,х,F: real;
Начало
вывод ('Введите значение переменной х ');
ввод (х);
а:=-1;
повторять
Если а < 0 то
если х≥0 тоначало
 ;
;
вывод ('F=',F,'a=',a);
конец
иначевывод ('значение F не определено');
если (0 < a) и (а < 1) то
если Сos(a2)<>0 то начало
F=Cos2(x)+(Sin(a2)/Cos(a2))3 ;
вывод ('F=',F,'a=',a);
конец
иначевывод ('значение F не определено');
если (1= < a) и (а < =2) товывод (' Функция не задана при а=',а);
если a > 2 то то
если х>0 тоначало
F=  ;
;
вывод ('F=',F,'a=',a);
конец
иначевывод ('значение F не определено');
а:=а+0,25;
до а>3
конец.
Тестирование алгоритма
Тестирование алгоритма
Шаг 0. Вводится значение переменной: х=1
Шаг 1. а=-1
Шаг 2. а < 0, переход к шагу 3 – проверке неявных условий, х≥0, условие выполняется, вычисляется значение функции по формуле  =-1-1=-2(шаг 4) и выводится результат: F=-2
=-1-1=-2(шаг 4) и выводится результат: F=-2
Шаг 3. (0 < a) и (а < 1); «ложь»
Шаг 4. (1= < a) и (а < =2); «ложь»
Шаг 5. (1= < a) и (а < =2); «ложь»
Шаг 6. a > 2; «ложь»
Шаг 7. а:=а+0,25;
Шаг 8. а>3; «ложь»; переход к шагу 2
Для того, чтобы проверить весь алгоритм, тестирование следует повторить при различных а, чтобы проверить разные интервалы.
Только после этого, можно сделать вывод, что алгоритм работает правильно
Практическое задание.
Выполнить постановку задачи и математическую модель, составит алгоритм, записав его в виде блок–схемы и псевдокода для вычисления значение выражения из таблицы
1. Протабулировать функцию

| 2. Протабулировать функцию

Где a,в – любые; х принадлежит [-3,3], шаг х=0.2 | ||||
3. Протабулировать функцию
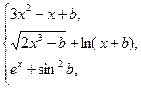
где b-любое; х принадлежит [-2,2], шаг х = 0,4 | 4. Протабулировать функцию
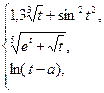
где t принадлежит [-3,3], шаг t = 0,1; а – любое. | ||||
5. Протабулировать функцию:

где х – любое; а принадлежит [-0,8; 1], шаг а=0,1. | 6. Протабулировать функцию

где х – любое, а принадлежит [-1,3], шаг а = 0,25 |
Контрольные вопросы.
- Что означает протабулировать функцию?
- Какой тип имеет циклический алгоритм в Вашем решении и почему?
- В чем отличие циклов "До" и "Пока"
Содержание отчета.
- Тема
- Цель
- Ответы на контрольные вопросы
- Выполненное практическое задание








