Решение.Этот определитель вычислим по правилу диагоналей. Приписываем справа к определителю первый и второй столбцы. Перемножаем элементы, стоящие на главной диагонали и складываем это произведение с аналогичными произведениями элементов, стоящих на диагоналях, параллельных главной. Затем к произведению элементов, стоящих на побочной диагонали, прибавляем аналогичные произведения элементов, стоящих на диагоналях, параллельных побочной. Затем от первой суммы вычитаем вторую. Это и будет искомый определитель.
1     2 3 1 2
4 5 6 4 5
7 8 9 7 8
| 
|
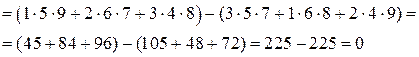
Ответ: 
б)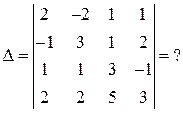 
Решение. Решение найдем разложением по первому столбцу, но сначала с помощью свойств определителя сделаем нули в этом столбце везде кроме элемента, равного минус единице.
Для этого элементы второй строки умножим на два и прибавим к соответствующим элементам первой строки; элементы второй строки прибавим к соответствующим элементам третьей строки; элементы второй строки умножим на два и прибавим к соответствующим элементам четвертой строки. Эти действия записываем так:
.
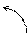
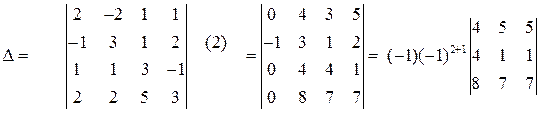Разложив определитель 4-го порядка по 1-му столбцу, свели его вычисление к нахождению одного определителя 3-го порядка, который можно вычислить по правилу диагоналей, разобранному выше. Можно дальше применить свойства определителя и свести этот определитель к одному определителю 2-го порядка. Продолжаем делать нули теперь уже во второй строке, умножая элементы третьего столбца на 
и прибавляя к первому и второму столбцам:
= 
(-4)
(-4)
Ответ: 
2) Умножить матрицы:
.
Решение. Произведение матриц получили, умножая элементы строк первой матрицы на соответствующие элементы столбцов второй матрицы и складывая их.
Ответ: 
.
3) Найти обратные матрицы:
а) 
.
Решение. Сначала находим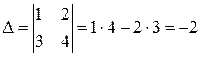 
; 
, значит, существует матрица 
. Находим алгебраические дополнения:
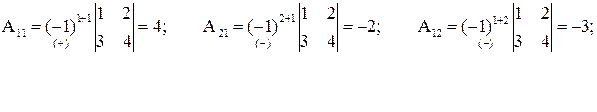
Ответ: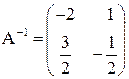 
.
4) Найти двумя способами ранг матрицы: 
.
Решение.
1 способ. Метод окаймляющих миноров. Находим любой минор второго по
рядка, отличный от нуля, например 
, по-
этому выписываем другой определитель 
. Нашелся определитель второго порядка, отличный от нуля, значит ранг 
. Теперь найдем определитель третьего порядка, окаймляющий найденный 
.
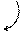
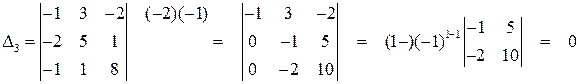
Берем другой определитель, окаймляющий 
, как и предыдущий.
Больше окаймляющих миноров третьего порядка для нет, поэтому ранг А, равный наивысшему порядку минора, отличного от нуля, равен двум.
способ. Метод элементарных преобразований.
.
Получили 2-е нулевые строки. Поэтому ранг А равен 2 (очевидно минор второго порядка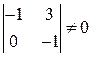 
).
Ответ: 
.
Контрольная работа № 2
“СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ”
ЗАДАНИЕ 1. Решить системы матричным способом и по формулам Крамера:
| 1. | а)  ;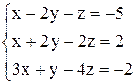
| б)  .
|
| 2. | а)  ;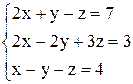
| б)  .
|
| 3. | а)  ;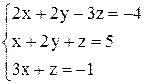
| б)  .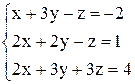
|
| 4. | a)  ;
| б)  .
|
| 5. | а)  ;
| б)  .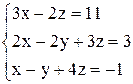
|
| 6. | а)  ;
| б)  .
|
| 7. | а)  ;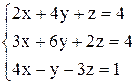
| б)  .
|
| 8. | а)  ;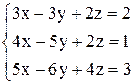
| б)  .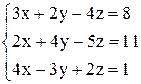
|
| 9. | а)  ;
| б)  .
|
| 10. | а)  ;
| б)  .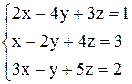
|
| 11. | а)  ;
| б)  .
|
| 12. | а)  ;
| б)  .
|
| 13. | а)  ;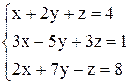
| б)  .
|
| 14. | а)  ;
| б)  .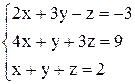
|
| 15. | а)  ;
| б)  .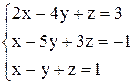
|
| 16. | а)  ;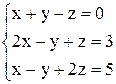
| б)  .
|
| 17. | а) ;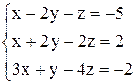
| б) .
|
| 18. | а) ;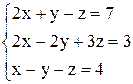
| б) .
|
| 19. | а) ;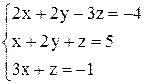
| б) .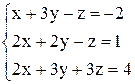
|
| 20. | a) ;
| б) .
|
| 21. | а) ;
| б) .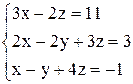
|
| 22. | а) ;
| б) .
|
| 23. | а) ;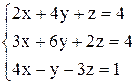
| б) .
|
| 24. | а) ;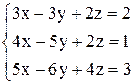
| б) .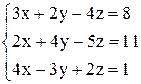
|
| 25. | а) ;
| б) .
|
| 26. | а) ;
| б) .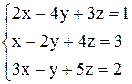
|
| 27. | а) ;
| б) .
|
| 28. | а) ;
| б) .
|
| 29. | а) ;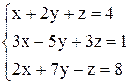
| б) .
|
| 30. | а) ;
| б) .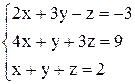
|
Задание 2. Решить системы методом Гаусса:
| 1. | а)  ;
| б)  ;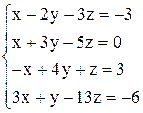
|
в)  ;
| г)  .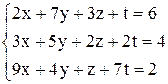
| |
| 2. | а)  ;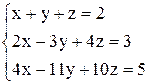
| б)  ;
|
в)  ;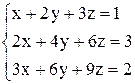
| г)  ;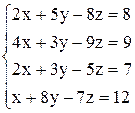
| |
| 3. | а)  ;
| б)  ;
|
в)  ;
| г)  .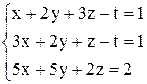
| |
| 4. | а)  ;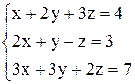
| б)  ;
|
в)  ;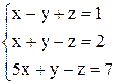
| г)  .
| |
| 5. | а)  ;
| б)  ;
|
в)  ;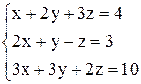
| г)  .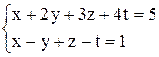
| |
| 6. | а)  ;
| б)  ;
|
в)  ;
| г) .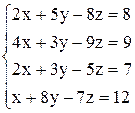
| |
| 7. | а)  ;
| б) ;
|
в)  ;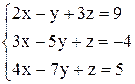
| г) .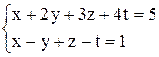
| |
| 8. 8. | а) ;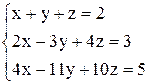
| б)  ;
|
в)  ;
| г)  .
| |
| 9. | а)  ;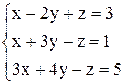
| б)  ;
|
в)  ;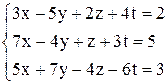
| г)  .
| |
| 10. | а)  ;
| б) ;
|
в)  ;
| г)  .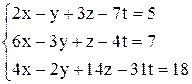
| |
| 11. | а)  ;
| б) ;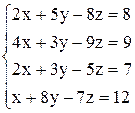
|
в)  ;
| г)  .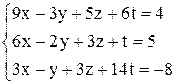
| |
| 12. | а)  ;
| б)  ;
|
в)  ;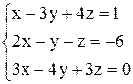
| г)  .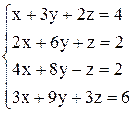
| |
| 13. | а) ;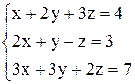
| б) ;
|
в)  ;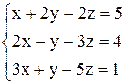
| г) .
| |
| 14. | а)  ;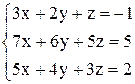
| б) ;
|
в)  ;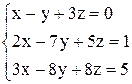
| г) .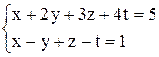
| |
| 15. | а) ;
| б) ;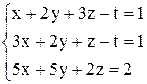
|
в)  ;
| г) .
| |
| 16. | а) ;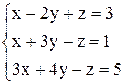
| б) ;
|
в)  ;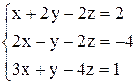
| г) .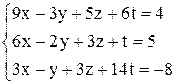
| |
| 17. | а) ;
| б) ;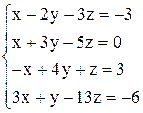
|
| в) ;
| г) .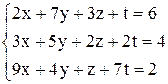
| |
| 18. | а) ;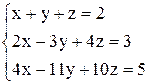
| б) ;
|
| в) ;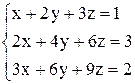
| г) ;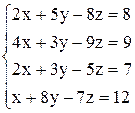
| |
| 19. | а) ;
| б) ;
|
| в) ;
| г) .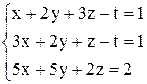
| |
| 20. | а) ;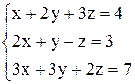
| б) ;
|
| в) ;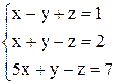
| г) .
| |
| 21. | а) ;
| б) ;
|
| в) ;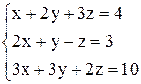
| г) .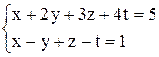
| |
| 22. | а) ;
| б) ;
|
| в) ;
| г) .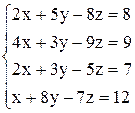
| |
| 23. | а) ;
| б) ;
|
| в) ;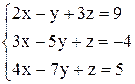
| г) .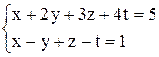
| |
| 24. | а) ;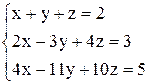
| б) ;
|
| в) ;
| г) .
| |
| 25. | а) ;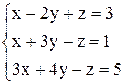
| б) ;
|
| в) ;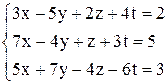
| г) .
| |
| 26. | а) ;
| б) ;
|
| в) ;
| г) .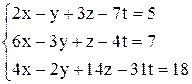
| |
| 27. | а) ;
| б) ;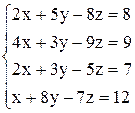
|
| в) ;
| г) .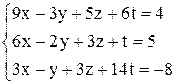
| |
| 28. | а) ;
| б) ;
|
| в) ;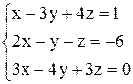
| г) .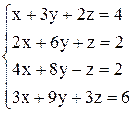
| |
| 29. | а) ;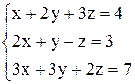
| б) ;
|
| в) ;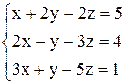
| г) .
| |
| 30. | а) ;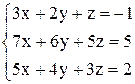
| б) ;
|
| в) ;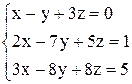
| г) .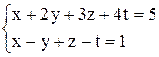
|
Задание 3. Решить системы однородных уравнений:
| 1. | а)  ;
| б)  .
|
| 2. | а)  ;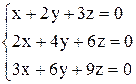
| б)  .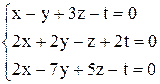
|
| 3. | а)  ;
| б)  .
|
| 4. | а)  ;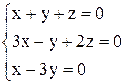
| б)  .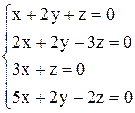
|
| 5. | а)  ;
| б)  .
|
| 6. | а)  ;
| б)  .
|
| 7. | а)  ;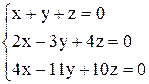
| б)  .
|
| 8. | а)  ;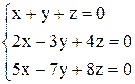
| б)  .
|
| 9. | а)  ;
| б)  .
|
| 10. | а)  ;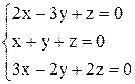
| б)  .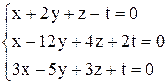
|
| 11. | а)  ;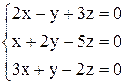
| б)  .
|
| 12. | а)  ;
| б)  .
|
| 13. | а)  ;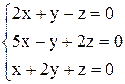
| б)  .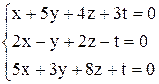
|
| 14. | а)  ;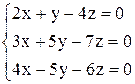
| б)  .
|
| 15. | а)  ;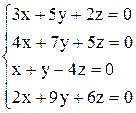
| б)  .
|
| 16. | а)  ;
| б)  .
|
| 17. | а) ;
| б) .
|
| 18. | а) ;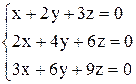
| б) .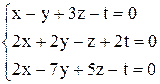
|
| 19. | а) ;
| б) .
|
| 20. | а) ;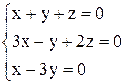
| б) .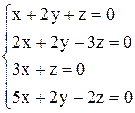
|
| 21. | а) ;
| б) .
|
| 22. | а) ;
| б) .
|
| 23. | а) ;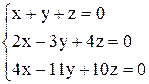
| б) .
|
| 24. | а) ;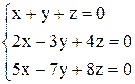
| б) .
|
| 25. | а) ;
| б) .
|
| 26. | а) ;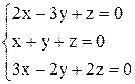
| б) .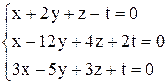
|
| 27. | а) ;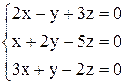
| б) .
|
| 28. | а) ;
| б) .
|
| 29. | а) ;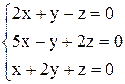
| б) .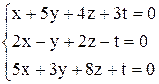
|
| 30. | а) ;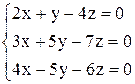
| б) .
|
Образец выполнения контрольной работы № 2
“СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ”
1) Решить систему матричным способом: 
.
Решение. Пусть 
. Тогда данную систему можно записать в виде матричного уравнения 
. Решаем его, домножая слева на обратную матрицу: 
Отсюда получаем решение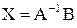 
. Найдем сначала 
.
.
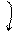
,значит 
).
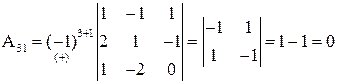
Составляем обратную матрицу
Найдем
,
т. е. 
.
Проверка. Подставим найденное решение в исходную систему: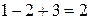 
(истина), 
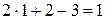(истина), 
(истина).
Ответ: 
.
2) Решить систему методом Крамера.
Возьмем эту же систему и решим её с помощью определителей.
|
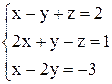, запишем определитель системы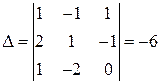 
Заменим в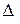 
столбец коэффициентов при 
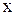на столбец правых частей
.
Заменим в 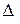столбец коэффициентов при 
на столбец правых частей
Заменим в столбец коэффициентов при 
на столбец правых частей
.
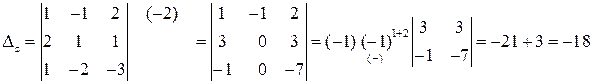По формулам Крамера получаем решение 
.
Ответ: .
3) Решить системы методом Гаусса:
а) 
Выписываем расширенную матрицу 
и с помощью элементарных преобразований приводим ее или к треугольному виду, или к виду трапеции (как получится).
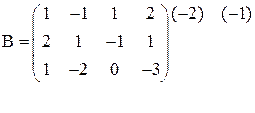
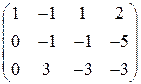(3)
x y z
|
. 
.
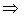
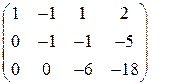
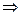
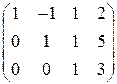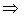
Так как число неизвестных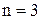 
и равно рангу системы, система имеет единственное решение. По полученной матрице восстанавливаем систему уравнений. Идя снизу вверх, получаем это решение: 
.
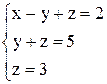Из последнего уравнения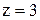 
3, с помощью второго находим 
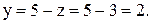Подставляя в первое уравнение найденные 
и 
находим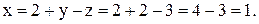 
Ответ: .
б) 
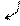
(-1)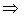 
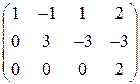
Следовательно, по теореме Кронекера-Капелли система несовместна (т. е. не имеет решения). Выпишем уравнение, соответствующее последней строке полученной матрицы: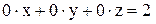 
, что невозможно.
Ответ: система не имеет решения.
в)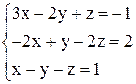 
Записываем расширенную матрицу:
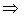
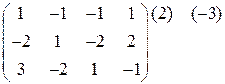
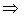
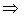
: (-1)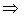 
.
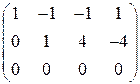. Отсюда следует, что система совместна.
Число неизвестных 
.Следовательно, система имеет бесконечное множество решений: 
. Отсюда система имеет одну свободную переменную, пусть это будет , тогда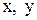 
– базисные (базисных неизвестных столько, каков ранг системы, т. е. сколько ненулевых строк остается в последней матрице).
Запишем систему, соответствующую полученной матрице: 
.
Следовательно, идя снизу вверх, выражаем базисные неизвестные через свободную . Из второго уравнения выражаем 
из первого уравнения
Общее решение: 
.
Из общего решения можно получить любое частное решение. Пусть 
, тогда получим частное решение: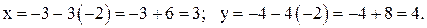 
Частное решение: 
.
Выполним проверку общего решения. Для этого подставим найденные выражения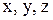 
в уравнения исходной системы:
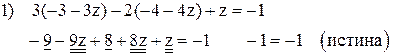
Ответ: .
