Действия с десятичными дробями.
При сложении и вычитании запятую записываем под запятой, уравниваем количество знаков после запятой, складываем как целые числа.
При умножении вычисляем, не обращая внимания на запятые, в результате отделить запятой столько знаков справа, сколько их было после запятой во всех множителях.
При делении перенести запятую в двух числах вправо на столько знаков, сколько их после запятой в делителе. Далее делить как целые числа, когда целая часть в делимом закончится, поставить запятую в частном и продолжить деление.
Противоположные и взаимообратные числа.
Противоположные числа – числа, отличающиеся только знаком. Например, 17 и – 17.
Взаимообратные числа – числа, произведение которых равно 1. Например, 17 и 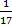 .
.
Отрицательные числа, действия с ними.
Сравнение отрицательных чисел: чем больше модуль отрицательного числа, тем меньше число. Отрицательное число всегда меньше 0 и любого положительного числа.
Сложение отрицательных чисел: сложить модули чисел и поставить знак минус.
Сложение чисел с разными знаками: из большего модуля вычесть меньший и поставить знак числа с большим модулем.
Вычитание отрицательных чисел и чисел с разными знаками: вычитание заменить сложением, изменив при этом знак вычитаемого.
Умножение и деление отрицательных чисел и чисел с разными знаками: умножить/разделить модули, поставить знак в соответствии с правилом: если количество минусов нечётное, то поставить знак минус, если количество минусов чётное, то поставить знак плюс.
Приведение подобных слагаемых.
Подобные слагаемые – слагаемые, отличающиеся только коэффициентами, буквенная часть при этом остаётся неизменной (её может не быть).
Привести подобные слагаемые: буквенную часть вынести за скобки, а с числовыми коэффициентами произвести соответствующие арифметические действия.
Одночлен, многочлен. Действия с ними.
Одночлен – это произведение чисел, переменных и их степеней с натуральными показателями.
Не являются одночленами: дроби с переменной в знаменателе, степени с отрицательными показателями.
Для записи одночлена в стандартном виде необходимо одинаковые переменные записать с помощью степени, далее расположить множители следующим образом: коэффициент, переменные в алфавитном порядке.
Степень одночлена – сумма показателей всех переменных.
Для умножения одночленов необходимо представить их произведение в стандартном виде.
Для возведения одночлена в степень нужно возвести в эту степень каждый множитель.
Многочлен – это сумма одночленов.
Стандартный вид многочлена – запись, при которой приведены подобные слагаемые и все одночлены записаны в стандартном виде, одночлены более высокой степени расположены левее одночленов более низкой степени.
Степень многочлена – наибольшая из степеней одночленов.
! При сложении и вычитании многочленов нужно помнить: если перед скобкой стоит знак минус, то все знаки в скобках меняются на противоположные.
Для умножения многочлена на одночлен нужно каждый член многочлена умножить на этот одночлен и произведения сложить, если это возможно.
Для умножения многочлена на многочлен нужно каждый член первого многочлена умножить на каждый член второго многочлена и произведения сложить, если это возможно.




