КУРСОВАЯ РАБОТА
по дисциплине
Компьютерные и информационные технологии в науке и производстве
Вариант №8
Студент группы МТМ-15 _________________ Шабров Г.Н.
Подпись, дата
Руководитель _________________ Равочкин А.С.
Подпись, дата
Рыбинск, 2016
Исходные данные
Определить зависимость изменения механических свойств латуни ЛС60-1 при высоких температурах. Спрогнозировать относительное удлинение δ, %, и предел прочности при растяжении σВ, кгс/мм2, при 800 °С.

Рисунок 1 – экспериментальные данные
Построение графиков по экспериментальным данным
В программе Microsoft Excel введем данные с рисунка в таблицу 1:
Таблица 1 – экспериментальные данные
| Предел прочности | Относительное удлинение | ||
| t, °С | s, кгс/см² | t, °С | δ, % |
По этим данным построим два графика для предела прочности при растяжении σВ и относительного удлинения δ (Рисунок 1,2).

Рисунок 2 – Графическая зависимость предела прочности от температуры
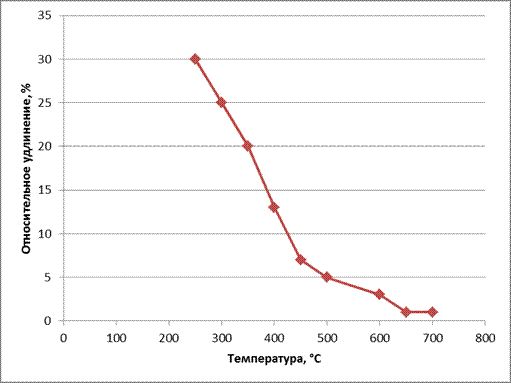
Рисунок 3 - Графическая зависимость относительного удлинения от температуры
Определение уравнения зависимости предела прочности от температуры
Для определния уравнения, описывающего зависимость предела прочности от температуры для каждого распределния построим линии тренда и выбирем из них наиболее подходящую по коэффициенту достоверности аппроксимации.

Рисунок 4 –Экспоненциальная аппроксимация

Рисунок 5 – Линейнаяная аппроксимация

Рисунок 6 – Логарифмическая аппроксимация

Рисунок 7 - Полиноминальная аппроксимация второй степени

Рисунок 8 - Полиноминальная аппроксимация шестой степени

Рисунок 9 – Степенная аппроксимация
Исходя из полученных коэффициентов аппроксимации для последующих расчетов принимаем уравнение полиноминальной апроксимации 6-й степени, поскольку коэффициент аппроксимации (R2) для данного уравнения наиболее приближен к 1.
Определение значения предела прочности при 800°С и построение графика зависимости предела прочности от температуры
Для определения значения предела прочности при растяжении (σВ) при температуре 800°С, а также для построения графика зависимости воспользуемся программой Mathcad.
Введем в качестве х значение температуры и вычислим значение предела прочности при данной температуре по ранее найденному уравнению полиноминальной аппроксимации шестой степени.
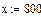
|
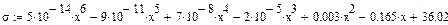
|

|
Использовать данное уравнение для расчета и построения графика невозможно, т.к. полученное значение предела прочности сильно отличается от экспериментальных данных.
Для определения предела прочности воспользуемся другими уравнениями аппроксимации. Произведем расчет для известных данных при температуре 700°С.
Проверим уравнение полиноминальной аппроксимации второй степени:

|

|
Проверим уравнение логарифмической аппроксимации:

|

|
Проверим уравнение степенной аппроксимации:
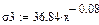
|

|
Проверим уравнение экспоненциальной аппроксимации:

|

|
Проверим уравнение линейной аппроксимации:

|

|
Будем использовать данное уравнение для построения графика, т.к. получившееся значение наиболее близко к экспериментальным данным, не смотря на самый низкий коэффициент аппроксимации (R2=0,006).

|
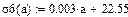
|

|
Рисунок 10 – График зависимости предела прочности (σ) от температуры (T)
Предел прочности при 800 ° С:
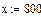
|

|

|




