I. Построение графика поверхности z=x2-y2 в диапазоне х Î[-2;2], y Î[-1;1] при шаге изменения аргументов D х= 0,2;D у= 0,2.
3.5.1. Провести табуляцию аргумента х:
- ввести в А2 число –2;
- ввести в А3 число –1,8;
- выделить ячейки А2:А3;
- поставить указатель мыши в правый нижний угол ячейки А3 (указатель примет вид тонкого крестика) и провести заполнение ячеек до А22.
3.5.2. Провести табуляцию аргумента у:
- ввести в В1 число –1;
- ввести в С1 число –0,8;
- выделить ячейки В1:С1;
- заполнить значениями аргумента у ячейки D1:L1.
3.5.3. Ввести формулы для вычисления Z:
- ввести в ячейку В2 формулу =$A2^2-B$1^2;
- скопировать формулу в ячейки В3:L22 и С2:L2.
Для этого следует скопировать формулу в ячейки В3:В22, затем выделить ячейки В2:В22 и скопировать весь выделенный столбец в ячейки С2:L22.
В результате получим табл. 3 (режим показа вычислений) и табл. 4 (часть табл. 3 в режиме показа формул).
Таблица 3
| A | B | C | D | E | F | G | H | I | J | K | L | |
| -1 | -0,8 | -0,6 | -0,4 | -0,2 | 0,2 | 0,4 | 0,6 | 0,8 | ||||
| -2 | 3,36 | 3,64 | 3,84 | 3,96 | 3,96 | 3,84 | 3,64 | 3,36 | ||||
| -1,8 | 2,24 | 2,6 | 2,88 | 3,08 | 3,2 | 3,24 | 3,2 | 3,08 | 2,88 | 2,6 | 2,24 | |
| -1,6 | 1,56 | 1,92 | 2,2 | 2,4 | 2,52 | 2,56 | 2,52 | 2,4 | 2,2 | 1,92 | 1,56 | |
| -1,4 | 0,96 | 1,32 | 1,6 | 1,8 | 1,92 | 1,96 | 1,92 | 1,8 | 1,6 | 1,32 | 0,96 | |
| -1,2 | 0,44 | 0,8 | 1,08 | 1,28 | 1,4 | 1,44 | 1,4 | 1,28 | 1,08 | 0,8 | 0,44 | |
| -1 | 0,36 | 0,64 | 0,84 | 0,96 | 0,96 | 0,84 | 0,64 | 0,36 | ||||
| -0,8 | -0,36 | 0,28 | 0,48 | 0,6 | 0,64 | 0,6 | 0,48 | 0,28 | -0,36 | |||
| -0,6 | -0,64 | -0,28 | 0,2 | 0,32 | 0,36 | 0,32 | 0,2 | -0,28 | -0,64 | |||
| -0,4 | -0,84 | -0,48 | -0,2 | 0,12 | 0,16 | 0,12 | -0,2 | -0,48 | -0,84 | |||
| -0,2 | -0,96 | -0,6 | -0,32 | -0,12 | 0,04 | -0,12 | -0,32 | -0,6 | -0,96 | |||
| -1 | -0,64 | -0,36 | -0,16 | -0,04 | -0,04 | -0,16 | -0,36 | -0,64 | -1 | |||
| 0,2 | -0,96 | -0,6 | -0,32 | -0,12 | 0,04 | -0,12 | -0,32 | -0,6 | -0,96 | |||
| 0,4 | -0,84 | -0,48 | -0,2 | 0,12 | 0,16 | 0,12 | -0,2 | -0,48 | -0,84 | |||
| 0,6 | -0,64 | -0,28 | 0,2 | 0,32 | 0,36 | 0,32 | 0,2 | -0,28 | -0,64 | |||
| 0,8 | -0,36 | 0,28 | 0,48 | 0,6 | 0,64 | 0,6 | 0,48 | 0,28 | -0,36 | |||
| 0,36 | 0,64 | 0,84 | 0,96 | 0,96 | 0,84 | 0,64 | 0,36 | |||||
| 1,2 | 0,44 | 0,8 | 1,08 | 1,28 | 1,4 | 1,44 | 1,4 | 1,28 | 1,08 | 0,8 | 0,44 | |
| 1,4 | 0,96 | 1,32 | 1,6 | 1,8 | 1,92 | 1,96 | 1,92 | 1,8 | 1,6 | 1,32 | 0,96 | |
| 1,6 | 1,56 | 1,92 | 2,2 | 2,4 | 2,52 | 2,56 | 2,52 | 2,4 | 2,2 | 1,92 | 1,56 | |
| 1,8 | 2,24 | 2,6 | 2,88 | 3,08 | 3,2 | 3,24 | 3,2 | 3,08 | 2,88 | 2,6 | 2,24 | |
| 3,36 | 3,64 | 3,84 | 3,96 | 3,96 | 3,84 | 3,64 | 3,36 |
Таблица 4
| A | B | C | D | E | |
| -1 | -0,8 | -0,6 | -0,4 | ||
| -2 | =$A2^2-B$1^2 | =$A2^2-C$1^2 | =$A2^2-D$1^2 | =$A2^2-E$1^2 | |
| -1,8 | =$A3^2-B$1^2 | =$A3^2-C$1^2 | =$A3^2-D$1^2 | =$A3^2-E$1^2 | |
| -1,6 | =$A4^2-B$1^2 | =$A4^2-C$1^2 | =$A4^2-D$1^2 | =$A4^2-E$1^2 | |
| -1,4 | =$A5^2-B$1^2 | =$A5^2-C$1^2 | =$A5^2-D$1^2 | =$A5^2-E$1^2 | |
| -1,2 | =$A6^2-B$1^2 | =$A6^2-C$1^2 | =$A6^2-D$1^2 | =$A6^2-E$1^2 | |
| -1 | =$A7^2-B$1^2 | =$A7^2-C$1^2 | =$A7^2-D$1^2 | =$A7^2-E$1^2 | |
| -0,8 | =$A8^2-B$1^2 | =$A8^2-C$1^2 | =$A8^2-D$1^2 | =$A8^2-E$1^2 | |
| -0,6 | =$A9^2-B$1^2 | =$A9^2-C$1^2 | =$A9^2-D$1^2 | =$A9^2-E$1^2 | |
| -0,4 | =$A10^2-B$1^2 | =$A10^2-C$1^2 | =$A10^2-D$1^2 | =$A10^2-E$1^2 | |
| -0,2 | =$A11^2-B$1^2 | =$A11^2-C$1^2 | =$A11^2-D$1^2 | =$A11^2-E$1^2 | |
| =$A12^2-B$1^2 | =$A12^2-C$1^2 | =$A12^2-D$1^2 | =$A12^2-E$1^2 | ||
| 0,2 | =$A13^2-B$1^2 | =$A13^2-C$1^2 | =$A13^2-D$1^2 | =$A13^2-E$1^2 | |
| 0,4 | =$A14^2-B$1^2 | =$A14^2-C$1^2 | =$A14^2-D$1^2 | =$A14^2-E$1^2 | |
| 0,6 | =$A15^2-B$1^2 | =$A15^2-C$1^2 | =$A15^2-D$1^2 | =$A15^2-E$1^2 | |
| 0,8 | =$A16^2-B$1^2 | =$A16^2-C$1^2 | =$A16^2-D$1^2 | =$A16^2-E$1^2 | |
| =$A17^2-B$1^2 | =$A17^2-C$1^2 | =$A17^2-D$1^2 | =$A17^2-E$1^2 | ||
| 1,2 | =$A18^2-B$1^2 | =$A18^2-C$1^2 | =$A18^2-D$1^2 | =$A18^2-E$1^2 | |
| 1,4 | =$A19^2-B$1^2 | =$A19^2-C$1^2 | =$A19^2-D$1^2 | =$A19^2-E$1^2 | |
| 1,6 | =$A20^2-B$1^2 | =$A20^2-C$1^2 | =$A20^2-D$1^2 | =$A20^2-E$1^2 | |
| 1,8 | =$A21^2-B$1^2 | =$A21^2-C$1^2 | =$A21^2-D$1^2 | =$A21^2-E$1^2 |
3.5.4. Построить график поверхности:
а) Выделите диапазон ячеек В2:L22;
б) Выполнить команды Вставка – Другие диаграммы Диаграмма – Поверхность В результате получим график поверхности (рис. 7).

Рис. 7. Построение диаграммы Поверхность
в) ввести Подписи горизонтальной оси А2:А22 см. пп. 3.4.3. в);
3.5.5. Теперь построим график функции  , где х Î[-5;5],
, где х Î[-5;5],
y Î[-5;5]; D x =1; D y =1.
а) Добавить новый рабочий лист в открытой книге Excel;
б) В ячейках А2:А12 провести табуляцию переменной х (аналогично п. 3.5.1);
в) В ячейках В1:L1 провести табуляцию переменной y (аналогично п. 3.5.2);
г) Для вычисления функции Z ввести формулы в ячейки В2:L22:
- в ячейку В2 ввести формулу =КОРЕНЬ($A2^2+B$1^2+1);
Можно для извлечения квадратного корня вместо функции КОРЕНЬ использовать возведение в дробную степень (1/2). Тогда формула будет выглядеть так: =($A2^2+B$1^2+1)^(1/2);
- Скопируем формулу из В2 в С2: L2 и В3:L12 (аналогично п. 3.5.3);
д) построить график поверхности аналогично п. 3.5.4. (получим рис. 8).
е) Провести редактирование диаграммы;
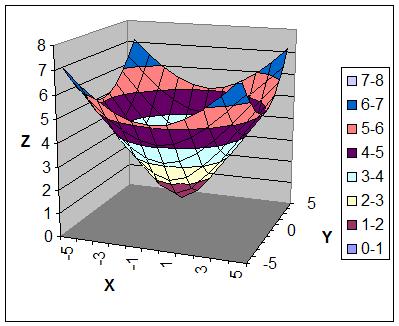
Рис. 8. График функции 
Выполнить команды Диаграмма – Объемный вид. Появится диалоговое окно (рис. 10). Пункт Объемный вид позволяет управлять подъемом обзора объемной диаграммы, ее углом поворота, перспективой и так далее.

Рис. 10 Диалоговое окно «Формат области диаграммы»
В появившемся диалоговом окне указываем угол поворота. В результате получаем рис. 11.
Редактировать график можно также при помощи курсора. С этой целью необходимо подвести курсор к элементу графика, например к стенке, и нажать правую клавишу мыши. В результате появится контекстное меню, с помощью которого можно ввести нужные изменения.

Рис. 11. График функции  после форматирования
после форматирования
4. Отчет по работе
Диаграммы и графики в распечатанном и электронном формате






