Детали, обрабатываемые на станках с ЧПУ, можно рассматривать как геометрические объекты.
При обработке детали инструмент и заготовка перемещаются относительно друг друга по определенной траектории.
Траектория инструмента это - путь который проходит инструмент (центр инструмента) во время обработки детали.
Траектория инструмента делится на отдельные участки опорными точками.
Опорная точка — точка расчетной траектории, в которой происходит изменение либо закона, описывающего траекторию, либо условий протекания технологического процесса.
Опорная геометрическая точка — точка расчетной траектории, в которой происходит изменение закона, описывающего траекторию.
Опорная технологическая точка — точка расчетной траектории, в которой происходит изменение условий протекания технологического процесса.
Опорная точка – это точка начало одного элемента и конца другого. Опорные точки обозначаются арабскими цифрами.
Программа обработки детали задает (описывает) движение определенной точки инструмента — как правило, его центра (Р).
Для концевой фрезы со сферическим торцом это центр полусферы, для концевой цилиндрической, сверла, зенкера, развертки — центр основания, для резцов — центр дуги окружности при вершине и т. д. (рис. 1.21).

Если радиус инструмента во время обработки детали по контуру остается постоянным, то траектория центра инструмента при контурной обработке является эквидистантой контуру детали (рис. 1.21 а — е).
Эквидистанта это геометрическое место точек, равноудаленных от контура детали на расстояние, равное радиусу Rи инструмента, строится справа или слева от элементов контура в зависимости от расположения инструмента относительно обрабатываемого контура.
Эквидистантной к дуге окружностиявляется дуга к этой окружностис тем же центральным углом (рис. а), а к отрезку прямой - отрезок, параллельный данному (рис. б).

Однако это встречается не всегда.

Траектория движения центра инструмента может существенно отличаться от линий контура детали (рис. 1.21, ж —л), так как в противном случае эквидистантное перемещение инструмента или перемещение инструмента точно по контуру привело бы к погрешности обработки.
Поэтому в ряде случаев под эквидистантой понимают такую траекторию движения центра инструмента, при которой обеспечивается обработка заданного контура. Движение по эквидистанте относится только к траектории рабочих ходов.
Перемещения центра инструмента при обработке детали могут быть также подготовительными и вспомогательными.
Характер этих движений во многом зависит от задаваемого в начале программирования положения исходной точки (нуля программы), от расположения приспособления и т. д.
Для обработки детали по программе необходимо определить рабочие, подготовительные и вспомогательные траектории перемещения центра принятого для работы инструмента.
Относительно контура обрабатываемой детали траектория движения центра инструмента при обработке может располагаться по-разному: совпадать с контуром, быть эквидистантой контуру, изменять положение относительно контура по определенному закону.
Для полной обработки детали (для выполнения заданной операции) траектория движения центра инструмента должна быть непрерывной. Разработать (определить) ее сразу как единое целое практически очень трудно, поскольку в общем случае программируемая траектория является достаточно сложной, определяющей перемещения центра инструмента в пространстве. Поэтому в практике программирования траекторию инструмента представляют состоящей из отдельных, последовательно переходящих друг в друга участков, причем эти участки могут быть или участками контура детали, или участками эквидистанты.
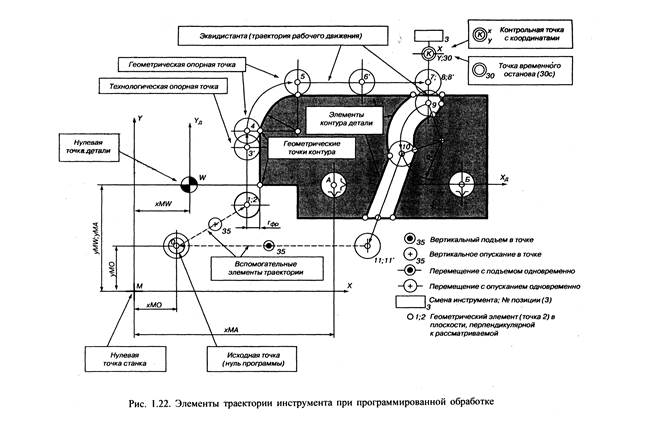
В общем случае участки траектории движения центра инструмента и траекторию в целом удобно представить графически, исходя из зафиксированного определенным образом положения контура обрабатываемой детали (рис. 1.22).
Отдельные участки контура детали и эквидистанты называются геометрическими элементами. К ним относятся отрезки прямых, дуги окружностей, кривые второго и высших порядков. Точки пересечения элементов или перехода одного элемента в другой находят как геометрические опорные (узловые) точки. Эти точки в большинстве случаев являются определяющими при задании положения элементов контура (эквидистанты) в пространстве. Это положение, так же, как и величина и направление движения инструмента, задается в системе координат с определенной заданной нулевой точкой.
Такая точка может быть у станка — нулевая точка станка (нуль станка) или у детали — нулевая точка детали (нуль детали). Она является началом системы координат данной детали.
В станках с ЧПУ представление детали и траектории ее обработки используют различные системы координат. Наиболее употребительны прямоугольные (декартовы), цилиндрические и сферические системы координат (рис. 1.23).

В прямоугольной системе координатами некоторой точки А называются взятые с определенным знаком расстояния х, у и z от этой точки до трех взаимно перпендикулярных координатных плоскостей. Точка пересечения координатных плоскостей называется началом координат, а координаты х, у, z — соответственно абсциссой, ординатой и аппликатой.
В цилиндрической системе координат положение точки в пространстве задается полярными координатами: радиусом р и центральным углом ᵠ (положение проекции точки на основной плоскости), а также аппликатой z — расстоянием от точки до основной плоскости.
В сферической системе координат точка задается длиной радиус-вектора R, долготой Ψ и полярным углом θ.
Переход из одной системы координат в другую осуществляется путем несложного Пересчета. Таким образом, в определенной системе координат контур детали и траектория перемещения центра инструмента относительно этого контура могут быть представлены геометрическими элементами с опорными точками, заданными координатами или в пространстве, или на плоскости (рис. 1.24).

На траектории движения центра инструмента могут быть назначены также технологические опорные точки, т. е. точки, где изменяются какие-то технологические параметры, например, подача инструмента, точки временного останова с указанием времени останова и т. д. (рис. 1.22).

При обработке детали инструмент может перемещаться или в одной плоскости — плоская обработка, при которой используются две управляемые координаты, или иметь сложное перемещение в пространстве — объемная обработка.
Однако чаще всего объемные поверхности деталей обрабатывают строчками, каждая из которых является плоской кривой. Опорные точки на траектории движения инструмента позволяют представить эту траекторию как определенную последовательность точек, проходимых центром инструмента (рис. 1.22) при обработке детали.
Каждое из положений (каждая опорная точка) в выбранной системе координат может быть определено числами, например, координатами. Сочетание таких чисел, определяющих ряд последовательных положений инструмента, или, иначе, ряд опорных точек траектории, и будет представлять основную часть программы работы станка, выраженную в числовом виде (рис. 1.24).
В начале программирования в системе координат детализадают положение базовых элементов заготовки (рис. 1.25, а).

Относительно нуля детали (точка W) задаются при программировании положение всех опорных точек, определяющих траекторию движения центра инструмента при обработке. При установке детали на станок (рис. 1.25, б) положение нуля детали (точки W) будет зафиксировано относительно координатной системы станка. Если при обработке детали используют приспособление (рис. 1.25, в), то оно должно быть закоординировано на станке относительно нуля станка (точки М). Система определяет координатную систему инструмента (рис. 1.25, б). Естественно, что при установке детали в приспособлении координатная система детали
должна совпадать с координатной системой приспособления (рис. 1.25, в).
При обработке детали при движении по элементам траекторий (прямым, дугам, кривым) в промежутках между опорными точками инструмент в определенных случаях может перемещаться по траектории, несколько отличающейся от заданной.
Однако можно задать такое число опорных точек, при котором отклонения фактической траектории от требуемой будут меньше некоторой наперед заданной величины, и деталь будет обработана в пределах заданной точности. Таким образом, начальный этап представления траектории обработки детали связан прежде всего с получением координат опорных точек траектории. Эти координаты могут быть выражены абсолютными размерами, т. е. для каждой опорной точки заданными относительно ну левой точки станка или детали (рис. 1.26, а), или задаваться в виде приращений в направлении движения инструмента от одной опорной точки к другой (рис. 1.26, б). При записи УП способ задания координат кодируется буквенно-цифровыми символами G90 (абсолютные координаты) и G91 (размеры в приращениях). Так, при перемещении центра инструмента (рис. 1.26, б) из точки W в точку 1 (размеры в приращениях) координата х изменится на величину ∆Х1, а координата у — на величину ∆У1 при дальнейшем движении из точки 1 в точку 2 приращение по оси X составит ∆Х2, по оси Y — ∆У2 и т. д.
. 

Задание координатами точек траектории движения центра инструмента зависит во многом от способа задания размеров детали (рис. 1.27). В большинстве систем ЧПУ работой станка управляют дискретно, с помощью импульсов. Цена одного импульса (наименьшее программируемое перемещение), или дискретность системы, отражает разрешающую способность комплекса, включающего систему ЧПУ, механизм подач и датчики обратной связи. В зависимости от дискретности системы размеры приращений координат между опорными точками траектории можно выразить не в мм, а количеством импульсов. Например, если дискретность по оси составляет 0,01 мм/имп., а по оси У — 0,02 мм/имп., то значения ∆Х и ∆У, равные, например, соответственно 12,85 мм и 8,6 мм, в импульсах будут выражены следующим образом: ∆Х = 1285 имп., ∆У = 430 имп.






