Тема 1. Пространство элементарных исходов. События. Действия с событиями. Вероятности событий. Вычисление вероятностей с применением элементов комбинаторики.
Задача 1. Монету бросили 3 раза. Событие А – решка выпала только один раз. Событие В – выпало не менее одного орла. Найдите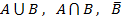 
Задача 2. Правильную монету бросают до появления орла или до трёх решек. Выпишите пространство элементарных исходов. Сколько в нем элементов? Какие вероятности следует приписать этим элементарным исходам?
Задача 3. Инвестиционный портфель состоит из двух ценных бумаг. Ежедневно фиксируется биржевая стоимость каждой из этих бумаг на момент закрытия биржи.
1) Опишите пространство элементарных исходов.
2) Опишите (изобразите) событие А: завтра цены на обе ценные бумаги повысятся.
3) Опишите (изобразите) событие В: завтра цены хотя бы на одну ценную бумагу повысятся.
Задача 4. Запишите, используя операции с событиями, что из двух событий А и В произошло только А.
Задача 5. Запишите, используя операции с событиями, что из трёх событий А, В и C произошли ровно два
Задача 6. Социологи, психологи, политологи, медики часто интересуются сочетанием у обследуемых тех или иных характеристик. Обозначим их через А и В. Пусть характеристика обозначает мужской пол, а характеристика В – наличие высшего образования.
1) Сформулируйте словами, кто составляет следующие подмножества обследуемых
а)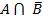 
б)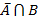 
в)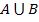 
2) Запишите, используя операции с событиями, следующие подмножества обследуемых:
а) женщины без высшего образования
б) женщины с высшим образованием и мужчины без высшего образования
в) мужчины и женщины без высшего образования
Задача 7. Преподаватель составляет контрольную работу, в которую входит по одной задаче из 5-ти различных тем (всего 5 задач). По каждой из этих тем у него существует 3 различных задачи. Сколько различных вариантов контрольной работы может составить преподаватель? (Варианты различны, если у них есть различные задачи хотя бы по одной теме).
Задача 8. Сколькими различными способами из группы 9-ти девушек и 5-ти юношей можно выбрать 3-х студентов так, чтобы среди них была одна девушка и двое юношей? (Порядок выбора не учитывать.)
Задача 9. На курсе некоторого факультета университета 6 групп. Сколькими способами можно распределить преподавание в этих группах между 3-мя преподавателями, если каждый из них должен получить 2 группы?
Задача 10. Сколько существует перестановок чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, в которых цифра 2 следует непосредственно за цифрой 1?
Задача 11. Тест состоит из 20 вопросов, на каждый из которых предложено 3 варианта ответа. Каждый вариант ответа на вопрос оценивается в нуль, один или два балла. Для подведения итогов теста вычисляется сумма баллов по всем данным ответам.
1) Сколько различных комбинаций ответов существует в этом тесте?
2) Сколько различных комбинаций ответов приводит в сумме к 39 баллам?
3) Сколько различных комбинаций ответов приводит в сумме к 38 баллам?
4) Сколько различных комбинаций ответов приводит в сумме к 37 баллам?
Задача 12. Игральную кость бросают 2 раза. Вычислите вероятности событий:
1) выпал дубль
2) на каждой кости выпало чётное число очков
3) на первой кости выпало больше очков, чем на второй.
Задача 13. В некотором эксперименте вероятность события А равна 0,7, а вероятность события В равна 0,4. Являются ли события А и В несовместными?
Задача 14. Какова вероятность того, что при бросании правильной игральной кости 3 раза номера всех выпавших граней будут различными?
Задача 15. Какова вероятность того, что при бросании правильной игральной кости 3 раза мы с каждым разом получаем грань с большим числом очков?
Задача 16. Правильную игральную кость бросают 3 раза. Вычислите вероятность того, что сумма очков меньше 6.
Задача 17. Пусть А и В – две противоположные вершины квадрата со стороной 1 см. В квадрате случайным образом выбираем точку. Какова вероятность того, что расстояние от этой точки до каждой из этих двух противоположных вершин меньше 1 см.?
Задача 18. На предприятие поступила партия из 12 труб, среди которых 2 трубы бракованные. Предприятие осуществляет выборочный контроль 3-x труб. Какова вероятность того, что хотя бы 1 бракованная труба будет проконтролирована?
Задача 19. В урне находится 100 лотерейных билетов, среди которых 5 выигрышных. Первый подошедший к урне вынимает из неё 3 билета. Какова вероятность того, что хотя бы один билет будет выигрышный?
Задача 20. Среди 8-ти кандидатов в мэры некоторого города 3 кандидата состоят в КПРФ, а 5– в ЕР. Для участия в дебатах было отобрано случайным образом 2 кандидата. Какова вероятность того, что хотя бы один из них состоит в ЕР?
Задача 21. Сколько различных перестановок можно составить из букв слова “программа”?
Задача 22. В каждой из 3-х коробок находятся ручки одного цвета. В разных коробках цвет ручек разный. Сколько существует различных вариантов выбора 7 ручек? (Варианты отличаются количеством ручек разного цвета.)
Тема 2. Независимые события. Условные вероятности.
Задача 1. Два признака А и В независимы. Вероятность встретить признак А у случайно выбранного респондента равна 0,6, а вероятность встретить признак В равна 0,8. Найти вероятность того, что у случайно выбранного респондента обнаружатся оба признака одновременно?
Задача 2. Два признака А и В независимы. Вероятность встретить признак А у случайно выбранного респондента равна 0,6, а вероятность встретить признак В равна 0,8. Найти вероятность того, что у случайно выбранного респондента обнаружится признак А, но не обнаружится признак В.
Задача 3. Два события А и В независимы.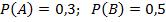 
. Чему равна вероятность того, что произойдёт хотя бы одно из этих событий?
Задача 4. Два признака А и В независимы. Вероятность встретить признак А у случайно выбранного респондента равна 0,2, а вероятность встретить признак В равна 0,6. Какова вероятность того, что у случайно выбранного респондента обнаружится только один из этих признаков?
Задача 5. Правильную игральную кость бросили 2 раза. Событие А состоит в том, что суммарное число очков меньше 5. Событие В – при первом броске выпала шестёрка. Являются ли события А и В независимыми?
Задача 6. Правильную игральную кость бросили 2 раза. Событие А состоит в том, что при первом броске выпало чётное число очков. Событие В – при втором броске выпало нечётное число очков. Являются ли события А и В независимыми?
Задача 7. Из колоды карт (их всего 52) случайным образом вытянули одну карту. Являются ли независимыми следующие события А и В: событие А – карта бубновой масти; событие В – король?
Задача 8. Правильную игральную кость бросили 2 раза. Найти вероятность того, что сумма выпавших очков не больше 4 при условии, что во втором броске выпало нечётное число очков.
Задача 9. Условная вероятность встретить у респондента признак А при условии, что у него обнаружился признак В, равна 0,7 (т.е.P(A|B)=0,7). Известно, что одновременно признаки А и В встречаются у 40% респондентов. Какова вероятность встретить у случайно выбранного респондента признак В?
Задача 10. Вероятность того, что ноутбук безотказно прослужит более 5 лет рана 0,7. Вероятность того, что ноутбук безотказно прослужит более 10 лет равна 0,3. Какова вероятность того, ноутбук, проработавший 5, проработает и 10 лет?
Тема 3. Формула полной вероятности и формула Байеса.
Задача 1. Вероятность совершения ошибки опытным операционистом банка при осуществлении стандартной операции равна 0,05, а вероятность совершения ошибки неопытным операционистом банка равна 0,15. В банке 80% опытных операционистов. Какой процент ошибок совершается в банке при осуществлении стандартных операций?
Задача 2. Некоторый кандидат баллотируется в областную думу по 2-м избирательным округам, находящимся в разных населённых пунктах, в которых он имеет разную степень популярности. Вероятность того, что он будет избран в первом населённом пункте, равна 0,4, во втором – 0,8. Предполагая. Что из всего числа участвовавших в голосовании избирателей в 1-ом населённом пункте проживает 40% избирателей, найдите вероятность того, что этот кандидат будет избран в областную думу.
Задача 3. На некотором предприятии вероятность брака равна 0,05. При контроле продукции этого предприятия совершаются ошибки: с вероятностью 0,01 бракованное изделие признается годным и с вероятностью 0,02 годное изделие признается бракованным. Случайно выбранное изделие было проконтролировано и признано бракованным. Какова вероятность, что это изделие годное?
Задача 4. В автомагазин поступают термостаты от трёх производителей, в количествах, которые находятся в пропорции 1:3:4 соответственно. На первом предприятии брак составляет 5%, на втором — 7%, на третьем — 4%.
1) Какой процент бракованных термостатов в автомагазине?
2) Если случайно выбранный в магазине термостат бракованный, то какова вероятность того, что он изготовлен на втором предприятии?
Задача 5. Среди студентов факультета 40% активно участвуют на семинарских занятиях по математике. Вероятность получить отличную оценку по математике студенту, который активно участвуют на семинарских занятиях по математике, равна 0,8. Вероятность получить отличную оценку по математике студенту, который не активен на семинарских занятиях по математике, равна 0,1.
1) Какой процент отличников по математике на факультете?
2) Предположим, что случайно выбранный студент – отличник. Какова вероятность того, что он не был активным на семинаре?
Задача 6. Компания по страхованию автомобилей подразделяет водителей на 3 класса:
Класс А (мало рискует), класс B (средне рискует), класс C (сильно рискует). Предположим, что количества застрахованных в этой компании относятся в классах А,В,С как 2:4:1. Вероятность водителю, отнесённому к классу А, попасть в аварию в течение года равна 0,01; отнесённому к классу В – 0,03; а отнесённому к классу С – 0,1.
1) Какой процент водителей, застрахованных в этой компании, попадает в аварию в течение года?
2) Предположим, что некоторый застрахованный в этой компании водитель попадает в аварию в течение года. Какова вероятность того, что он относится к классу С?
Тема 4. Схема Бернулли
Задача 1. Правильная игральная кость бросается 4 раза. Какова вероятность того, что грань с шестёркой выпадет хотя бы два раза?
Задача 2. Контрольная работа состоит из 4-х тестовых вопросов. На каждый из вопросов приведено 3 варианта ответа, среди которых только один правильный. За каждый правильный ответ начисляется 1 балл. Какова вероятность того, что при выборе наугад ответа на каждый вопрос, студент получит хотя бы 3 балла?
Задача 3. Какая вероятность больше: выиграть у равносильного соперника (например, в шахматы) 3 партии из 4-х или 5 партий из 8-ми? (Ничьи не учитывать).
Тема 5. Вычисление математического ожидания и дисперсии
Задача 1. За неделю цены на один и тот же товар повысились в 30% торговых точек. Случайно были отобраны 10 торговых точек. Каковы ожидаемое число (математическое ожидание) и стандартное отклонение в этой выборке числа торговых точек, в которых цены повысились?
Задача 2. Правильную монету бросили 50 раз. Найдите математическое ожидание и дисперсию числа выпавших гербов.
Задача 3. Правильную игральную кость бросили 12 раз. Найдите математическое ожидание и дисперсию числа выпавших шестёрок.
Задача 4. Для независимых случайных величин X и Y отметьте правильные варианты преобразований дисперсии:
Задача 5. У студента в связке 3 ключа, внешне неразличимые, но только один из них подходит к замку двери квартиры. Чтобы открыть дверь в квартиру, он случайным образом выбирает ключ из связки. Если ключ не подошёл к замку, попытка повторяется. При этом не подошедший ключ в дальнейших попытках не участвует. Найдите распределение числа попыток открытия двери. Найдите математическое ожидание этого распределения.
Задача 6. Студент может поехать на занятия или на автобусе, или на маршрутке. Вероятность поездки на маршрутке в 2 раза больше, чем на автобусе. Билет на автобус стоит 30 руб., а на маршрутку – 45 руб. Найти математическое ожидание и дисперсию стоимости одной поездки на транспорте.
Тема 6. Нормальное распределение.
Используя таблицу для функции распределения стандартной нормальной величины, вычислите следующие вероятности.
Задача 1. Пусть случайная величина Z имеет стандартный нормальный закон распределения, т.е.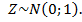 
Найти:
1) 
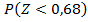
2) 
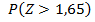
3) 
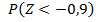
4) 
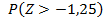
5) 
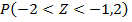
6) 
7) 
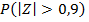
8) 
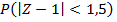
Задача 2. Пусть случайная величина X имеет нормальный закон распределения с математическим ожиданием m и дисперсией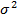 
, т.е. 
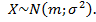(В каждой задаче величины m и 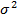заданы.)
Найти:
1)Пусть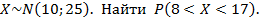 
2)Пусть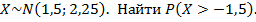 
3)Пусть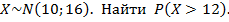 
4) Пусть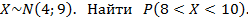 
5)Пусть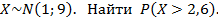 
Задача 3. Есть акции 2-х компаний. Их ежедневные цены на бирже X и Y имеют нормальное распределение со средним 100 руб. и стандартным отклонением 5 руб. и независимы. Один инвестор купил на 200 руб. акции первой компании, второй – на те же деньги акцию первой и акцию второй компаний. Найти вероятност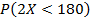и: 
и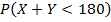 
. У какого инвестора вероятность понести убытки меньше?
Задача 4. Рост девушек-студенток распределён по нормальному закону с математическим ожиданием 168 см. и дисперсией 36 см2. Выбираем случайным образом двух девушек. Какова вероятность того, что хотя бы одна из двух девушек имеет рост, меньше 165 см.?
Задача 5. В магазин поступила большая партия пачек печенья. Вес пачки печенья – случайная величина, распределённая по нормальному закону с математическим ожиданием 200 г. и дисперсией 49 г2. Случайно выбираем 2 пачки печенья. Какова вероятность того, что хотя бы одна пачка имеет вес меньше 192 г.
Задача 6. Прибор, измеряющий скорость автомобилиста, имеет погрешность, которая распределена по нормальному закону с нулевым математическим ожиданием (т.е. без систематической ошибки) и стандартным отклонением 2 км/час. Автомобилист будет оштрафован, если прибор зафиксирует скорость, которая превышает допустимую на данном участке скорость на 20 км/час. Какова вероятность того, что автомобилист, превысивший скорость на 22 км/час не будет оштрафован по замерам этого прибора? Какова вероятность того, что автомобилист, превысивший скорость на 18 км/час будет оштрафован по замерам этого прибора?
Тема 7. Теорема Муавра-Лапласа
Задача 1. В некотором городе 60% жителей не удовлетворены работой ЖКХ. Вычислите приближённо вероятность того, что среди 640 случайно выбранных жителей не больше 230 человек удовлетворены работой ЖКХ.
Задача 2. Известно, что процент потребителей некоторого товара равен 20%. Вычислите приближённо вероятность того, что при случайном опросе 500-ти респондентов более 120-ти заявят, что они являются потребителями этого товара.
Задача 3. Вычислите приближённо вероятность того, что при 225 бросаниях правильной монеты орёл выпадет не более 100 раз.
Задача 4. Известно, что мэру некоторого города доверяют 70% горожан. Вычислите приближённо вероятность того, что в результате репрезентативного социологического опроса среди 500 опрошенных горожан окажется не менее 365 доверяющих мэру горожан.
Задача 5. В некотором регионе 40% избирателей голосуют за некоторую партию. Какова вероятность того, что из 100 случайно отобранных избирателей хотя бы 45 избирателей проголосуют за эту партию?
Задача 6. В некотором городе 60% квартир имеют стационарное подключение к Интернету. Вычислите приближённо вероятность того, что среди 100 случайно выбранных квартир хотя бы 65 квартир подключены к Интернету.
