Расчет элементов загрузочных устройств
1. Объем накопителя
Объем накопителя Wδ определяется по следующей формуле:

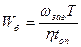
 ,
,
где: Wб – объем накопителя (трубы, шахты, бункера и др.), в см3;
Wзаг – объем одной заготовки, см3;
Т – время автоматической работы станка, мин.
η- коэффициент заполнения накопителя заготовками. Для различных заготовок η колеблется в пределах 0,2…0,8.
Поскольку производительность загрузочного устройства Q равна

 ,
,
то выразим объем накопителя через производительность


 ,
,
2. Время t перемещения заготовки по наклонному лотку
Во время перемещения заготовки из т.О (состояния покоя) в т.А на нее действуют силы
G – вес;
Y – сила инерции;
F – сила трения;
N – реакция.
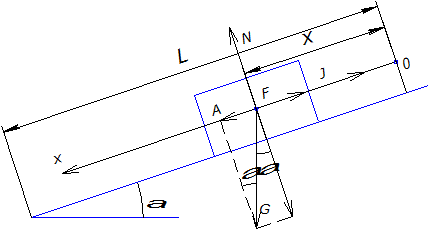
Рис. 16.1. Расчетная схема для определения t
Выбрав направление оси Х, напишем уравнение движения заготовки
G sinα = F + Y,
где:  – угол наклона лотка;
– угол наклона лотка;
G = mg;
F =  G cosα =
G cosα =  mg cosα;
mg cosα;
Y = m  ;
;
m – масса заготовки, кг;
g – ускорение силы тяжести, 9,8 м/сек2;
 – коэффициент трения;
– коэффициент трения;
 – ускорение заготовки, м/сек2.
– ускорение заготовки, м/сек2.
Зная, что  (V – скорость заготовки, м/сек.), напишем дифференциальное уравнение движения заготовки
(V – скорость заготовки, м/сек.), напишем дифференциальное уравнение движения заготовки
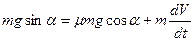 .
.
Сократим на m, и, разделив переменные, получим
dv = g sinα dt – μg cosα dt
Проинтегрировав, получим:
V = dt sinα – μgt cosα + C1.
при х = 0, V = 0, t = 0, значит C1 = 0
V = gt(sinα – μ cosα).
Поскольку  (х – путь, м), то подставив в последнее уравнение получим:
(х – путь, м), то подставив в последнее уравнение получим:
dx = (sinα – μ cosα)gt dt.
Проинтегрировав, получим:
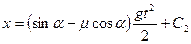 .
.
Найдем С2, подставив начальные условия х = 0, t = 0, значит и С2 = 0.
Тогда время перемещение заготовки
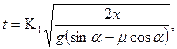
При качении:

где:  - приведенный коэффициент трения.
- приведенный коэффициент трения.
Теперь найдем время перемещения заготовки из т. О в т. А. Для этого введем в последнюю формулу коэффициент К1, учитывающий трение по боковым сторонам лотка, а вместо х напишем его значение L:
 .
.
Рекомендуются следующие значения:
при скольжении μ = 0,1…0,2
αmin = 25o ÷ 30o,
при качении заготовок  К1 = 1,5 ÷ 1,8
К1 = 1,5 ÷ 1,8
α = 5о ÷ 7о.
О приведенном коэффициенте трения
При движении заготовки по угловому лотку (рис.16.2.) имеем следующие зависимости:

Рис. 16.2. Расчетная схема для определения приведенного коэффициента трения при движении по угловому лотку



Величина  называется приведенным коэффициентом трения.
называется приведенным коэффициентом трения.
Тогда 
Поэтому для перемещения заготовок в угловом лотке требуются большие силы, чем в плоском лотке, следовательно угловой лоток должен иметь больший угол наклона, чем плоский.
Обычно угол α > 25о, ширина бортов b = (0,7…0,8)d
при m до 5 кг β = 45о
при m свыше 5 кг, β = 60о
Условие незаклинивания заготовок при их движении по наклонному лотку
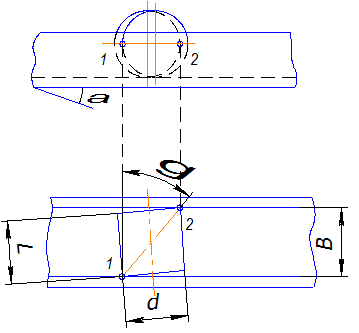
Рис. 16.3. Расчетная схема для определения ширины лотка (гладкая деталь катится по дну лотка)
Пусть по наклоненному лотку перемещается цилиндрическая заготовка диаметром d. Зазор между боковыми стенками лотка и заготовкой
S = B – l
Заготовка может касаться стенок лотка в двух точках: 1 и 2. Зазор S следует выбирать таким, чтобы не было заклинивания.
Если угол перекоса заготовки γ окажется меньше или равным углу трения 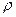 , то заготовка заклинится в лотке.
, то заготовка заклинится в лотке.
tgγ ≤ tg 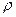 = μ.
= μ.
Если больше – то будет перемещаться по лотку без заклинивания, т.е.
tgγ > tg 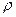 = μ.
= μ.
Условия начала заклинивания
tgγ = tg 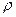 = μ,
= μ,
μ – коэффициент трения.
Из рисунка можно получить: 
Из тригонометрии известно, что 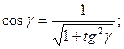
при заклинивании, т.е. при tg γ = μ, получим  ,
,
Тогда 
 .
.
Чтобы заготовка не заклинивалась, следует уменьшить зазор между нею и боковыми сторонами лотка. Это получится, если выбранная ширина лотка B будет меньше ее значения, соответствующего заклиниванию, и в тоже время больше
l + Smin

Обычно в левую часть неравенства вставляют наименьшие предельные значения (d и  , а Smin берут из
, а Smin берут из  ). Расчет правой и левой части дает пределы, в которых должна находиться ширина лотка B.
). Расчет правой и левой части дает пределы, в которых должна находиться ширина лотка B.
В случае перемещения ступенчатой заготовки по лотку (рис. 16.4) в формулу для определения B входит диаметр Dф.
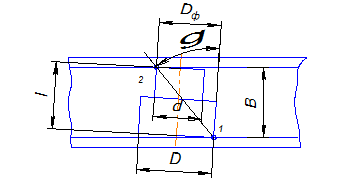
Рис.16.4. Расчетная схема для определения ширины лотка в случае перемещения ступенчатой заготовки
Случай, когда по лотку перемещается заготовка с цапфами (рис. 16.5).


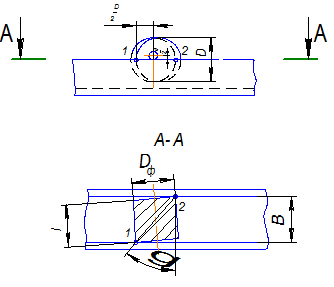
Рис.16.5. Перемещение ступенчатой заготовки, опирающейся цапфами о бортик лотка






