| Параметр | Полупроводник | |
| Кремний | Германий | |
| Заряд ядра | ||
| Атомный вес | 28,1 | 72,6 |
| Диэлектрическая проницаемость (отн. ед.) | ||
Эффективная масса электронов 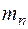 (отн. ед.) (отн. ед.)
| 0,33 | 0,22 |
Эффективная масса дырок  (отн. ед.) (отн. ед.)
| 0,55 | 0,39 |
Ширина запрещенной зоны  , В , В
| 1,11 | 0,67 |
Эффективная плотность состояний 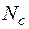 , , 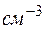
| 
| 
|
Эффективная плотность состояний  , , 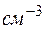
| 
| 
|
Подвижность электронов  , , 
| ||
Подвижность дырок  , , 
| ||
Собственное удельное сопротивление  , , 
| 
| 
|
Собственная концентрация 
| 
| 
|
Коэффициент диффузии электронов 
| ||
Коэффициент диффузии дырок 
| ||
Критическая напряженность поля 
| ||
Критическая напряженность поля 
| ||
Максимальная скорость, 
| 
| 
|
Приведенные в таблице 1 параметры соответствуют комнатной температуре.
Таблица 2
Основные физические константы, используемые в теории полупроводников
| Основные физические константы | Приближенные значения |
| Элементарный заряд | 
|
| Масса свободного электрона | 
|
| Постоянная Планка | 
|
| Постоянная Больцмана | 
|
| Электрическая постоянная (диэлектрическая проницаемость вакуума) | 
|
| Магнитная постоянная (Магнитная проницаемость вакуума) | 
|
| Число Авагадро (количество атомов в 1 грамм-атоме вещества) | 
|
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
Задача 1. Рассчитать величину температурного потенциала в полупроводнике в интервале температур. Построить графики и дать физическое объяснение полученных результатов.
Требуется рассчитать значения температурного потенциала  при изменении температуры от –400 до 500 С.
при изменении температуры от –400 до 500 С.

 , (1)
, (1)
где К - постоянная Больцмана, Т – абсолютная температура, q - заряд электрона.
Умножив и разделив правую часть выражения (1) на То=300 К (комнатная температура) получим
 , (2)
, (2)
где  - температурный потенциал при комнатной температуре.
- температурный потенциал при комнатной температуре.
Новая форма записи не только уменьшает время, которое требуется для проведения расчетов, но и делает формулу более наглядной с точки зрения зависимости температурного потенциала от температуры.
Разобьем весь температурный диапазон на 10 точек.
Для каждой точки рассчитаем температурный потенциал, и результаты сведем в таблицу 3.
Таблица 3
| T, К | ||||||||||
 , мВ , мВ
| 19.1 | 20.8 | 20.6 | 22.5 | 23.3 | 24.2 | 25.7 | 26.5 |
По данным таблицы строим график рис.1
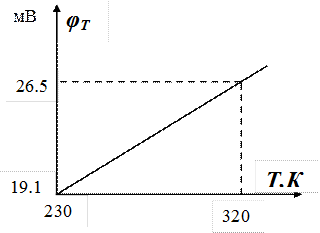
Рис.1
Из выражения 2 следует, что температурный потенциал является линейной функцией от температуры, следовательно, для построения графика достаточно было вычислить значения температурного потенциала для двух значений температуры.
Выводы.
С физической точки зрения температурный потенциал характеризует в электрических единицах статистическую температуру или кинетическую энергию электрона в вакууме или электронном газе. С повышением температуры кинетическая энергия электрона растет, что приводит к увеличению температурного потенциала. Кроме того, можно сделать заключение, что при температуре полупроводника T=0 температурный потенциал равен нулю, а, следовательно, кинетическая энергия электронов и дырок равна нулю и электронов в зоне проводимости нет. Валентные уровни все заполнены. Таким образом, нет свободных подвижных зарядов в полупроводнике и его проводимость равна нулю. Это заключение справедливо для любого типа полупроводника.
ЛИТЕРАТУРА
1.Ицкович В.М. Электроника. Учебное пособие. – Томск: Томский государственный университет, 2006. – 360 с.
2. Степаненко И.П. Основы микроэлектроники: Учебное пособие для вузов. – 2-е изд., перераб. и доп. - М.: Лаборатория Базовых Знаний, 2001.- 488 с.






