Лекция. Основные показатели надежности авиационной техники
Вопрос 1. Вероятностные показатели надежности
В процессах проектирования, изготовления, испытания и эксплуатации AT для решения различных инженерных задач необходимы количественные характеристики надежности. Время работы изделий до отказа зависит от множества причин, что позволяет рассматривать количество отказов и время их появления в качестве случайных величин. Именно случайность появления событий является характерной особенностью проблем, возникающих при исследовании надежности объектов эксплуатации. Поэтому для изучения закономерностей появления таких событий в теории надежности использованы теория вероятностей и математическая статистика.
Отказ изделия трактуют как случайное событие, а время его работы до возникновения отказа 
— случайной величиной. Таким образом, отказ представляет собой событие, при котором случайная величина меньше заданного времени работы изделия 
. При 
отказ изделия в течение времени не возникнет.
В качестве основной количественной меры надежности объектов, характеризующей закономерности появления отказов во времени, принимают вероятность безотказной работы 
(функция надежности):
.
В теории вероятности и математической статистике вероятностью события 
называется число 
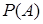, характеризующее возможность появления события.
При известных значениях общего количества наблюдаемых изделий 
и количества работоспособных изделий 
в момент времени вероятность работоспособной работы можно определить по формуле
Вероятность отказа (функция распределения) определяют как вероятность того, что время безотказной работы меньше заданного времени :
.
При известных значениях общего количества наблюдаемых изделий и количества неработоспособных изделий 
в момент времени вероятность отказа можно определить по формуле
Так как при любом значении наработки изделие может быть или работоспособным, или потерявшим работоспособность, то
, 
.
На практике необходимо определять вероятность безотказной работы систем ВС в течение полета при условии их исправности и готовности к выполнению полетного задания, т. е. определять вероятность безотказной работы системы на отрезке времени, если к началу рассматриваемого отрезка система не отказала.
Для характеристики скорости изменения надежности объектов эксплуатации используют плотность распределения времени безотказной работы:
Если случайная величина имеет плотность распределения 
, то
.
Примерный вид функций , 
и 
и их взаимосвязь показаны на рис. 111. Особенностью кривой является то, что площадь под кривой всегда равна единице: 
.
Рис.111. Примерный вид функций , 
и и их взаимосвязь
В дополнение к функциям , , , 
часто используют для неремонтируемых объектов среднюю наработку до отказа 
:
.
Последний интеграл соответствует площади под графиком функции надежности .
Вопрос 2.. Интенсивность отказов. Виды законов распределения
. Интенсивностью отказов называется отношение числа отказавших изделий в единицу времени к среднему числу изделий, исправно работающих в данный отрезок времени. Вероятностная оценка этой характеристики находится из выражения
.
Очень часто встречается следующая запись этой характеристики:
.
Это уравнение называется основным дифференциальным уравнением надежности.
В теории надежности наибольшее распространение получили следующие законы распределения случайных величин f(t):
для дискретных случайных величин - биноминальный закон; закон Пуассона;
для непрерывных случайных величин - экспоненциальный закон; нормальный закон; гамма-распределение; закон Вейбулла;
Напомним, что период приработки характеризуется высокой интенсивностью отказов, вызванных отклонением от требований конструкторско-технологической документации, Он подчиняется распределению Вейбулла.
Распределение Вейбулла – двухпараметрический закон с параметрами 
и 
( - параметр формы кривой распределения; - параметр масштаба).
Этот закон является универсальным, так как при соответствующих значениях параметров превращается в нормальное, экспоненциальное и другие виды распределений. Закон Вейбулла удовлетворительно описывает наработку до отказа подшипников, элементов радиоэлектронной аппаратуры, его используют для оценки надежности деталей и узлов машин, в частности автомобилей, а также для оценки надежности машин в процессе их приработки.
Графики зависимости характеристик закона Вейбулла от наработки приведены на рис.115.
Рис.115. Зависимости характеристик закона Вейбулла от наработки
Период нормальной эксплуатации описывается экспоненциальным законом распределения, называемым также основным законом надежности, постепенные отказы еще не проявились и надежность характеризуется внезапными отказами. Эти отказы вызываются неблагоприятным стечением многих обстоятельств и поэтому имеют постоянную интенсивность. Экспоненциальное распределение находит довольно широкое применение в теории массового обслуживания, описывает распределение наработки на отказ сложных изделий, время безотказной работы элементов радиоэлектронной аппаратуры.
Графики зависимости характеристик экспоненциального закона от наработки приведены на рис.116.
Рис.116. Зависимости характеристик экспоненциального закона от наработки
Период старения или износа характеризуется резким увеличением интенсивности износовых отказов, которые подчиняются нормальному закону распределения (закону Гаусса).
Этот закон играет важную роль и наиболее часто используется на практике по сравнению с другими законами распределения. Основная особенность этого закона состоит в том, что он является предельным законом, к которому приближаются другие законы распределения. В теории надежности его используют для описания постепенных отказов, когда распределение времени безотказной работы в начале имеет низкую плотность, затем максимальную и далее плотность снижается.
Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие, примерно равнозначные факторы.
Графики зависимости характеристик нормального закона от наработки приведены на рис.117.
Рис.117. Зависимости характеристик нормального закона от наработки
