Соединение с обратной связью имеет прямую цепь передачи сигнала и цепь обратной связи. Обратная связь может быть отрицательной и положительной. При отрицательной обратной связи на вход прямой цепи подается разность межу входным сигналом х(t) и выходным сигналом линии обратной связи. При положительной обратной связи эти величины складываются.

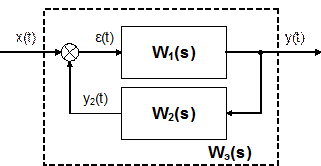
Для соединения с отрицательной обратной связью справедливы следующие соотношения:
Y(s) = W1(s)·E(s) = W1(s)·[X(s) – Y2(s)] Y2(s) = W2(s)·Y(s)
Y(s) = W1(s)·X(s) – W1(s)·Y2(s) = W1(s)·X(s) – W1(s)·W2(s)·Y(s)
Y(s) + W1(s)·W2(s)·Y(s) = Y(s)·[1 + W1(s) ·W2(s)] = W1(s)·X(s)
Y(s) = W1(s)/[1 + W1(s)·W2(s)]·X(s)
В итоге получаем следующее выражение для эквивалентной (результирующей) передаточной функции:
Wэ(s) = W1(s)/[1 + W1(s)·W2(s)]
Для случая соединения с положительной обратной связью получается аналогичное выражение для эквивалентной передаточной функции, только при этом знак плюс в знаменателе изменяется на знак минус:
Wэ(s) = W1(s)/[1 – W1(s)·W2(s)]
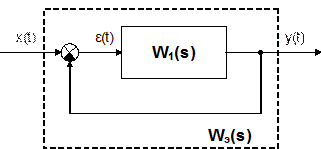
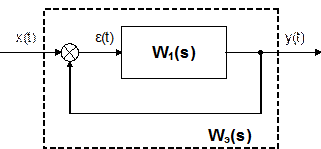
Частным случаем соединения с обратной связью является ситуация, когда выходной сигнал от прямой цепи передается без изменения на элемент сравнения или сумматор. Такие обратные связи называются единичными, т.к. у них передаточная функция в обратной цепи равна единице (W2(s) = 1). Тогда эквивалентные передаточные функции для отрицательной и положительной обратной связи упрощаются и принимают следующий вид, соответственно:
Wэ(s) = W1(s)/[1 + W1(s)]
Wэ(s) = W1(s)/[1 – W1(s)]
Правила преобразования структурных схем
В тех случаях, когда структурная схема оказывается слишком сложной, например, содержит перекрестные связи, ее упрощают пользуясь правилами преобразования структурных схем. Смысл этих правил состоит в переносе элементов структурной схемы из одного положения в другое, так чтобы при этом сохранялась эквивалентность структурных схем.
1. Перенос узла через звено.
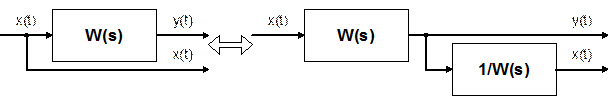
Чтобы перенести узел через звено с передаточной функцией W(s), необходимо включить в линию, не проходящую через звено (выход 2), дополнительный элемент – звено с передаточной функцией 1/W(s). Убедимся, что эти схемы эквивалентны. Действительно, сигнал у(t) после такого переноса не изменится, а сигнал на выходе 2 будет равен: Х(s)·W(s)·1/W(s) = Х(s), т.е. он совпадает с исходным сигналом х(s).
2. Перенос звена через узел.
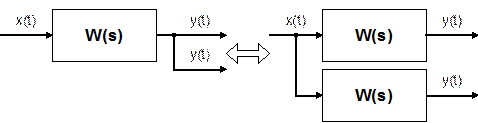
Чтобы перенести звено с передаточной функцией W(s) через узел, необходимо включить в обе линии звенья с передаточной функцией W(s). Легко убедиться, что эквивалентность структурных схем при этом сохраняется.
3. Перенос сумматора через звено.
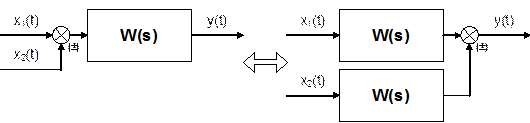
Сразу отметим, что данное правило преобразования структурных схем применимо как к сумматорам, так и к элементам сравнения, т.к. элемент сравнения можно рассматривать как сумматор с инвертированным входом.
Чтобы перенести сумматор через звено с передаточной функцией W(s), необходимо к обоим входам на сумматор добавить дополнительный элемент – звено с передаточной функцией W(s). Убедимся, что эти схемы эквивалентны. Выходной сигнал на исходной схеме равен: Y(s) = W(s)·[X1(s) ± X2(s)]; выходной сигнал на преобразованной схеме равен: Y(s) = W(s)X1(s) ± W(s)X2(s), т.е. выходные сигналы совпадают.
4. Перенос звена через сумматор.

Это правило преобразования структурных схем также применимо как к сумматорам, так и к элементам сравнения. Чтобы перенести звено с передаточной функцией W(s) через сумматор, необходимо в линию без звена (вход 2) включить дополнительный элемент – звено с передаточной функцией 1/W(s). Убедимся, что эти схемы эквивалентны. Выходной сигнал на исходной схеме равен: Y(s) = W(s)·X1(s) ± X2(s); выходной сигнал на преобразованной схеме равен: Y(s) = W(s)·[X1(s) ± 1/W(s)·X2(s)] = W(s)·X1(s) ± X2(s), т.е. выходные сигналы совпадают.
5. Перенос узла через сумматор.
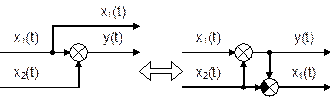
Чтобы перенести узел через сумматор, необходимо в схему включить дополнительный элемент – элемент сравнения. Эти схемы эквивалентны, т.к. выходные сигналы совпадают: у(t) = х1(t) + х2(t) и х1(t) = у(t) – х2(t) = х1(t) + х2(t) – х2(t).
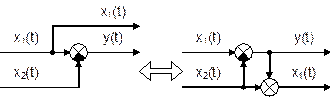
При применении этого правила преобразования структурных схем для переноса узла через элемент сравнения в схему необходимо включить дополнительно не элемент сравнения, а сумматор. Эквивалентность этих схем также легко проверить: у(t) = х1(t) – х2(t) и х1(t) = у(t) + х2(t) = х1(t) – х2(t) + х2(t).
6. Перенос сумматора через узел.
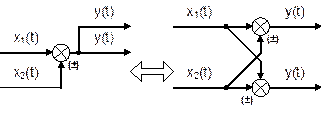
Это правило преобразования структурных схем применимо как к сумматорам, так и к элементам сравнения. Чтобы перенести сумматор через узел, необходимо в схему включить дополнительный сумматор. Эти схемы эквивалентны, т.к. выходные сигналы совпадают: у(t) = х1(t) + х2(t).
7. Перенос сумматора через сумматор.
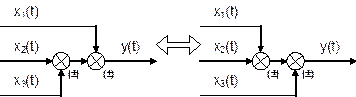
Это правило преобразования структурных схем фактически реализует правило коммутативности сложения в математике – от перестановки мест слагаемых сумма не изменяется. Оно, разумеется, применимо как к сумматорам, так и к элементам сравнения.
8. Перенос звена через звено.

Это правило преобразования структурных схем фактически реализует правило коммутативности умножения в математике – от перестановки мест множителей произведение не изменяется.
9. Перенос узла через узел.
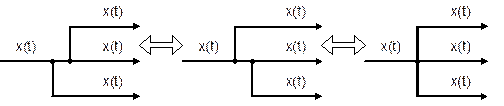
Это правило настолько очевидно, что не имеет смысла его комментировать.






