Пояснения к расчетам
1. К расчету цикла теплового двигателя.
1.1. Для расчета газовой смеси изучить раздел «Идеальные газовые смеси». Идеальная газовая смесь подчиняется:
a) закону Дальтона: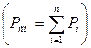 
, Па где Pi - парциальное давление i-гo
компонента, Па; an- число компонентов в смеси;
b) уравнению Клапейрона-Менделеева: 
Pсм Vсм=mсмRсмT, где 
масса смеси,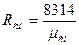 
, Дж/(кг×К) - удельная газовая постоянная смеси,
mсм,кг/кмоль - «кажущаяся» молекулярная масса смеси.
Характеристики смеси, необходимые для расчетов процессов и цикла в целом (mсм,
Rcm, Cv см, Cp см), определяются через массовый или объемный состав смеси по формулам:
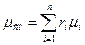, кг/кмоль (
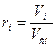- объемная доля i-ro компонента);
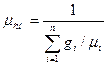, кг/кмоль(
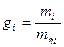- массовая доля i-гo компонента);
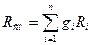, Дж/(кгК) - где 
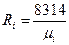Дж/(кг×К) - удельная газовая постоянная i-гo компонента, а mi, кг/кмоль - молекулярная масса i-гo компонента.
Связь между массовыми и объемными долями определяется соотношениями;
;
.
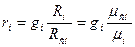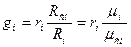Пример расчета газовой смеси.
Атмосферный воздух состоит приближенно по объему из 21% кислорода и 79% азота. Определить молекулярную массу данной смеси, ее удельную газовую постоянную и массовый состав. Определить плотность и удельный объем воздуха при нормальных физических условиях.
Решение.
Так как по условию задачи известен объемный состав газовой смеси (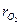
= 0,21,
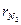=0,79), то по формуле 
находим
mвозд = 
= 0,21·32+0,79·28=29, кг/кмоль;
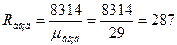, Дж/(кгК).
Так как 
, то
;
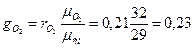Удельный объем воздуха при нормальных физических условиях (Рну = 760 мм Hg =101300Па, tну = 0°С = 273К) находим по уравнению Клапейрона-Менделеева для массы m = 1 кг газовой смеси:
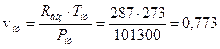, м3/кг
Плотность воздуха при этих условиях:
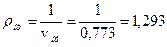, кг/м3.
1.2 Расчет параметров состояния (Р, v, T) в характерных точках цикла и термодинамических процессов требует изучения особенностей политропного и изопроцессов, составляющих цикл. Базовыми уравнениями и формулами для решения этой задачи являются:
- уравнение Клапейрона-Менделеева Pv = Rсм×Т;
- уравнения политропного процесса [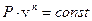 
, 
, 
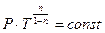] для расчета параметров состояния при известном показателе политропы n, или для расчета показателя политропы "n" при известных параметрах состояния;
- формула для расчета изменения внутренней энергии ∆u = Cv × (Tкон - Tнач) ,кДж/кг,
где Тнач – температура смеси в начальной точке процесса, Ткон – температура смеси в конечной точке процесса;
- формула для расчета изменения энтальпии ∆h = Ср × (Ткон - Тнач) ,кДж/кг;
- формула для расчета изменения энтропии ∆s =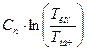 
,кДж/(кг-К);
- формула для расчета работы изменения объема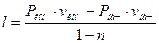 
, кДж/кг;
- формула для расчета теплоты q = Сn ×(Ткон - Тнач), кДж/кг;
- формулы для расчета теплоемкостей смеси (Cv - изохорная теплоемкость и Ср –изобарная теплоемкость) через массовый состав смеси и значения соответствующих теплоемкостей для каждого компонента смеси:
; 
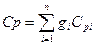
Cp -Cv =R - (уравнение Майера).
Так как в данных расчетах теплоемкости для каждого компонента Cvi и Срi, считают независимыми от температуры, то их определяют по молекулярно-кинетической теории газов через число степеней свободы N:
; 
,
для одноатомных газов N = 3;
для двухатомных газов N = 5 (включая воздух);
для трех- и более атомных газов N = 6.
Теплоемкость рабочего тела в процессе
;
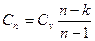где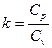 
–показатель адиабаты для смеси.
Пример расчета изохорной и изобарной теплоемкостей воздуха.
Решение. Так как массовый состав воздуха по приближенным расчетам (см. задачу
выше)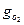 
= 0,232; 
=0,763, то
, Дж/(кг×К)
Cp=Cv+R=717.1+287=1004.1, Дж/(кг×К)
Показатель адиабаты для воздуха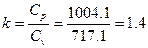 
1.3. Расчеты q1, q2 и lц основаны на учете знаков теплоты и работы в каждом процессе:
+q и +ℓ, - соответственно, подведенное к рабочему телу тепло и работа расширения;
-q и -ℓ - соответственно, теплота, отводимая от рабочего тела, и работа на сжатие рабочего тела.
- Термический КПД цикла
- Термический КПД цикла Карно
;
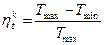где Tmax - максимальная температура рабочего тела в цикле; Tmin - минимальная температура рабочего тела в цикле.
Примечание. При построении цикла в s-T координатах рекомендуется за начальное состояние рабочего тела (состояние 1) принять точку с координатами (s1=0, T1). Для построения остальных характерных и промежуточных точек цикла используются значения температур в конкретных состояниях и расчетные значения изменений энтропии ∆s (с учетом знака ∆s).
К расчету цикла парокомпрессионной холодильной установки.
- Расчет цикла и ответы на поставленные вопросы требуют изучения принципов работы и анализа процессов холодильных установок. При определении параметров состояний хладагента на линии насыщения необходимо воспользоваться соответствующими таблицами в приложениях, где:
s', h' - значения энтропии и энтальпии кипящего хладагента (на линии X=0);
s'', h'' - значения энтропии и энтальпии сухого насыщенного пара хладагента (на линии X=1).
- Расчет параметров состояний влажного насыщенного пара хладагента (0< X <1), а при необходимости и степени сухости X, производится с использованием известных соотношений для конкретного давления P:
sx = s'+X· (s''-s');
hx =h''+ X·(h''-h').
- Удельная холодопроизводительность холодильной установки 
, кДж/кг
определяет количество тепла, отводимое от охлаждаемой среды в единицу времени одним килограммом хладагента (процесс 4-1); G, кг/с – расход хладагента.
- Теоретическая мощность двигателя установки
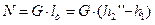, кВт.
-Холодильный коэффициент цикла холодильной машины
.
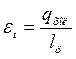- Холодильный коэффициент обратного цикла Карно в интервале температур цикла:
.
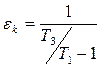Литература
1. Теплотехника. Учебник для химико-технологических специализированных вузов. /А.В.Чечеткин, Н.А. Занемонец/ М. ВШ., 1986 – 344с.
2. Теплотехника. Учебник для вузов. /А.П.Баскаков и др./ М. Энергоиздат, 1991 – 224с.
3. Основы технической термодинамики. Учебник для вузов. /В.В. Мурзаков/, М., «Энергия», 1973, 304с.
4. Холодильные установки. /Е.С. Курылев и др./ М. Политехника, 1999 – 576с.
