Модуль 2
Лекция 8. Комплексные числа
8.1.Понятие комплексного числа. Мнимая единица
8.2.Комплексная плоскость Арифметические операции над комплексными числами
8.3. Модуль и аргумент комплексного числа. Тригонометрическая форма записи
8.4.Корень из комплексного числа. Корни из единицы
8.5. Комплексно сопряженные числа
Программные положения
Комплексные числа являются расширением понятия действительных чисел. В приложениях они облегчают многие задачи, в том числе действия над векторами
Методические рекомендации
Обратите внимание на понятие мнимой единицы и правила действий с комплексными числами, особенно правило умножения
Литература
А.В.Дорофеева «Высшая математика» Глава IV, § 4.5 стр. 83-90
Б.П.Демидович, В.А.Кудрявцев Глава XVI «Комплексные числа» стр.299-304
Дополнительно
Р.Курант, Г.Роббинс «Что такое математика?» глава II §5 стр.116-129
Контрольные вопросы
1) Что такое комплексное число?
2) Какие комплексные числа называются равными?
3) Какое число называется комплексно сопряженным данному?
4) Сформулируйте правила действий с комплексными числами
5) Вычислите
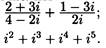
6)Изобразите на комплексной плоскости множества точек
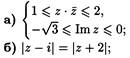
7) Как записать комплексное число в тригонометрической форме?
8) Выведите формулу корня n-й степени из комплексного числа
9) Отметьте на единичной окружности корни 4 степени из 1
10) Обоснуйте свойства сопряженных чисел
Понятие комплексного числа. Мнимая единица
Определение 8.1 (1).
Рассмотрим элементы вида z = x + y·i (или просто z=x+yi), где х и у — действительные числа, а i — некоторый элемент, называемый мнимой единицей. Элемент z = х + y·i называют комплексным числом, х — его действительной, а у — мнимой частью и пишут x = Re z (от латинского realus — действительный), у = Im z (imaginarius — мнимый).
Два комплексных числа считаются равными тогда и только тогда, когда равны их действительные и мнимые части.
Вместо х + 0·i и 0 + у·i пишут соответственно х и y·i, в частности, 0 + 0·i = 0; вместо 1·i пишут i. Число х + y·i, у которого y≠ 0, называют существенно комплексным числом, а число вида y·i, у ≠ 0, — чисто мнимым.
Замечания 8.1.
1) Исторически мнимая единица возникла из необходимости извлечения корня из отрицательного числа. Обозначение i было введено для специального случая – нахождения корней уравнения х2 = -1. Оно имеет два решения, x = i и x = -i, так что мнимая единица i такова, что i2 = -1
2) x+i·y – это единое число, а не действие сложения. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: z=yi+x или переставить мнимую единицу: z=y+i·x – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: z=x+yi
Пример 8.1 (1).
z 1= 2 + 3i, z 2= - 1 – 5i, z3 = -10i, z4= 8
Определение 8.1.(2)
Комплексное число 
= x – yi называется (комплексно) сопряженным числу
z = x + yi (подробнее см.п.8.5)
Пример 8.1 (2).
z 1= 2 + 3i,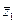 
= 2 – 3i
z 2= - 1 – 5i,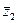 
= -1 +5i
z3 = -10i, 
= +10i
z4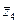= 8, 
= 8
Множество всех комплексных чисел обозначают через С.
Комплексная плоскость Арифметические операции над комплексными числами
С помощью операций сложения и умножения действительных чисел в множестве комплексных чисел также можно ввести операции сложения и умножения.
Для комплексных чисел z1 = х1 + y1i и z2 = х2 + y2i их сумма z1 + z2 определяется как комплексное число, действительная и мнимая части которого получаются в результате сложения соответственно действительных и мнимых частей чисел z1 и z2.
z1 + z2 = (х1 + х2 ) + (y1+y2)i
Для определения произведения комплексных чисел сначала определим квадрат мнимой единицы:
i2 = ii = -1
а затем — произведение двух произвольных комплексных чисел
z1 = х1 + y1i и z2 = х2 + y2i как результат почленного умножения z1 = х1 + y1i на z2 = х2 + y2i с использованием соотношения i2 = —1 и
последующего сложения полученных результатов:
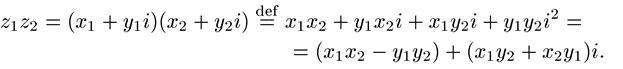Замечание 8.2.
При определении умножения комплексных чисел можно было бы предварительно не определять, что i2 = —1, и не использовать правила почленного умножения, а сразу определить произведение по формуле B.3). Тогда из нее бы уже следовало,
что i2 = —1. В самом деле,
ii = (0 + 1·i)(0 + 1·i) = -1
Вычитание определяется как действие, обратное сложению: z = z1 - z2 если
z1 = z2 +z, а деление — как действие, обратное умножению: z = z1 / z2, если z1 = z2 z
Примеры 8.2.
1. Сложить два комплексных числа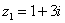 
, 
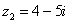
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:
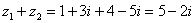
2. Найти произведение комплексных чисел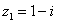 
, 
,
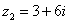
Поскольку - i·6i = -6i2 = 6
Векторная интерпретация. Каждому комплексному числу z = x + yi соответствует упорядоченная пара действительных чисел (x, у), и наоборот, каждой упорядоченной паре действительных чисел (x, у) соответствует комплексное число z = x + yi, и эти
соответствия взаимно однозначны. С упорядоченными же парами действительных чисел (x, у) на плоскости (при фиксированной системе декартовых координат) находятся
во взаимно однозначном соответствии векторы этой плоскости, имеющие числа х и у
своими координатами. В результате комплексное число z = х + yi можно рассматривать как вектор на плоскости с координатами x, у (см. рис 8.2.(1)).
Рис. 8.2.(1)
Этот вектор мы будем обозначать той же буквой z =(x,y)
Примеры 8.2. (см. рис. 8.2.(2))
Построим на комплексной плоскости следующие комплексные числа:
, 
, 
, 
, 
, 
, 
, 
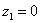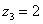
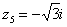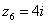
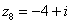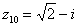
Рис. 8.2.(2)
Целесообразность такой интерпретации комплексных чисел следует из того, что при сложении комплексных чисел складываются и соответствующие им векторы: при сложении векторов их координаты складываются, поэтому суммой векторов z1 = х1 + y1i и z2 = х2 + y2i их суммой является вектор z = z1 + z2 = (x 1+ x 2, y 1+ y2) (правило параллелограмма, см рис. 8.2.(3))
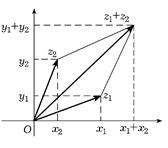
Рис. 8.2.(3)
Поскольку вычитание как для комплексных чисел, так и для векторов является действием, обратным сложению, то при вычитании комплексных чисел соответствующие им векторы также вычитаются (см.8.2.(4))
Рис. 8.2.(4)
Определение 8.2.
Координатная плоскость, векторы z = (x, у) которой интерпретируются как комплексные числа, называется комплексной плоскостью, ее ось x — действительной осью (обозначается Re z), а ось у — мнимой (Im z)).
