Пропорциональное звено описывается алгебраическим уравнением:
у(t) = K·х(t)
Физическая реализация звена.
Примерами таких пропорциональных звеньев могут служить, рычажный механизм, жесткая механическая передача, редуктор, электронный усилитель сигналов на низких частотах, делитель напряжения и др.


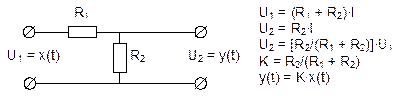
Переходная функция.
Переходная функция пропорциональное звена имеет вид:
h(t) = L-1[W(s)/s] = L-1[K/s] = K·1(t)
Весовая функция.
Весовая функция пропорционального звена равна:
w(t) = L-1[W(s)] = K·δ(t)




Рис. 3.5. Переходная функция, весовая функция, АФЧХ и АЧХ пропорционального звена.
Частотные характеристики.
Найдем АФЧХ, АЧХ, ФЧХ и ЛАХ пропорционального звена:
W(jω) = K = K +0·j
A(ω) =  = K
= K
φ(ω) = arctg(0/K) = 0
L(ω) = 20·lg[A(ω)] = 20·lg(K)
Как следует из представленных результатов, амплитуда выходного сигнала не зависит от частоты. В действительности ни одно звено не в состоянии равномерно пропускать все частоты от 0 до ¥, как правило на высоких частотах, коэффициент усиления становится меньше и стремиться к нулю при ω → ∞. Таким образом, математическая модель пропорционального звена является некоторой идеализацией реальных звеньев.
Апериодическое звено I-ого порядка
Апериодические звенья иначе еще называются инерционными.
Передаточная функция.
Передаточная функция апериодического звена I-ого порядка имеет вид:
W(s) = K/(T·s + 1)
где K – коэффициент усиления; T – постоянная времени, характеризующая инерционность системы, т.е. продолжительность переходного процесса в ней. Поскольку постоянная времени характеризует некоторый временной интервал, то ее величина должна быть всегда положительной, т.е. (T > 0).
Математическое описание звена.
Апериодическое звено I-ого порядка описывается дифференциальным уравнением первого порядка:
T·dу(t)/dt + у(t) = K·х(t)
Физическая реализация звена.
Примерами апериодического звена I-ого порядка могут служить: электрический RC-фильтр; термоэлектрический преобразователь; резервуар с сжатым газом и т.п.
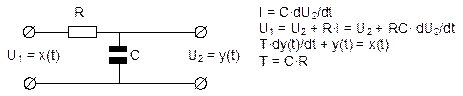

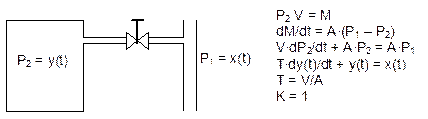
Переходная функция.
Переходная функция апериодического звена I-ого порядка имеет вид:
h(t) = L-1[W(s)·1(t)] = L-1[K/(s·(T·s + 1))] = K – K·e-t/T = K·(1 – e-t/T)


Рис. 3.6. Переходная характеристика апериодического звена I-го порядка.
Переходный процесс апериодического звена I-ого порядка имеет экспоненциальный вид. Установившееся значение равно: hуст = K. Касательная в точке t = 0 пересекает линию установившегося значения в точке t = T. В момент времени t = T переходная функция принимает значение: h(T) ≈ 0.632·K, т.е. за время T переходная характеристика набирает только около 63% от установившегося значения.
Определим время регулирования Tу для апериодического звена I-ого порядка. Как известно из предыдущей лекции, время регулирования – это время, после которого разница между текущим и установившимся значениями не будет превышать некоторой заданной малой величины Δ. (Как правило, Δ задается как 5 % от установившегося значения).
h(Tу) = (1 – Δ)·hуст = (1 – Δ)·K = K·(1 – e-Tу/T), отсюда е-Tу/T = Δ, тогда Tу/T = -ln(Δ), В итоге получаем Tу = [-ln(Δ)]·T.
При Δ = 0,05 Tу = - ln(0.05)·T ≈ 3·T.
Другими словами, время переходного процесса апериодического звена I-ого порядка приблизительно в 3 раза превышает постоянную времени.
Весовая функция.
Весовая функция апериодического звена I-ого порядка имеет вид:
w(t) = L-1[W(s)] = L-1[K/(T·s + 1)] = (K/T)·e-t/T

Рис. 3.7. Весовая функция апериодического звена I-го порядка.
Для весовой функции апериодического звена I-ого порядка характерен скачок в начальный момент времени t = 0. Это происходит из-за того, что на вход звена подается δ-функция. Поскольку δ-функция – это математическая абстракция, которую на практике можно смоделировать в виде короткого импульса, то в реальном, физически реализуемом процессе будет наблюдаться переходный процесс, обозначенный на рисунке пунктиром.
Частотные характеристики.
Найдем АФЧХ, АЧХ, ФЧХ и ЛАЧХ апериодического звена I-ого порядка:
W(jω) = K/(T·jω + 1) = K·(T·jω – 1)/[(T·jω + 1)·(T·jω – 1)] =
= K·(T·jω – 1)/(-T2ω2 – 1) = K/(T2ω2 + 1) – [KTω/(T2ω2 + 1)]·j
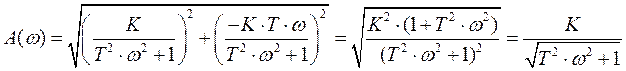





Рис. 3.8. АФЧХ, АЧХ, ФЧХ, ЛАХ и ЛФХ апериодического звена I-ого порядка.
ЛАХ апериодического звена I-ого порядка представляет собой трансцендентную функцию. Чтобы упростить использование ЛАХ, вводят понятие асимптотических ЛАХ, то есть кусочно-линейных функций, не сильно отличающихся от истинных.
Переход к асимптотической ЛАХ: заменяем истинную ЛАХ – ломаной асимптотической. Выделим области низких и высоких частот и по отдельности рассмотрим поведение ЛАХ в этих областях. После чего, оценим максимальную ошибку, возникающую на границе областей.
Область низких частот: T2w2 <<1; т.е. w<<1/T; можно пренебречь выражением T2w2. Получаем: L(w) = 20lgK. Это горизонтальная прямая.
Область высоких частот: T2w2 >>1; т.е. w>>1/T; можно пренебречь 1 в сравнении с выражением T2w2. Получаем L(w) = 20lgK – 20lgTw. Это – уравнение прямой с наклоном -20дБ/декаду. (В логарифмических координатах декада – это интервал, соответствующий изменению частоты в 10раз).
Точке пересечения этих прямых соответствует частота ω1 = 1/T, которая называется частотой сопряжения. Вычислим максимальную ошибку ЛАХ в этой точке:
DLmax = (20lgK) – [20lgK + 10lg(T2w12+1)] = -10lg2» -3 дб.
Следует заметить, что ошибка асимптотической ЛАХ апериодического звена I-ого порядка не зависит от параметров звена (K и T) и равна приблизительно –3 дб.






