Аффинные преобразования плоскости. Виды аффинных преобразований. Классификация аффинных преобразований. Группа аффинных преобразований и ее подгруппы.

Лекция №17

Определение 17.1. Преобразование плоскости называется аффинным, если оно любые три точки 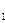М 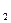, М , М 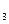, лежащие на одной прямой, переводит в три точки 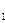М` 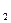, М` , М` 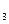, также лежащие на одной прямой, при этом сохраняя простое отношение трех точек.

Преобразование подобия является аффинным преобразованием.

Лемма 17.2. Если аффинные преобразования 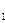f и f 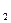переводят две точк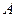и и 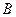соответственно в точки 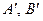, то образы точки М при этих преобразованиях совпадают, где 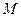- любая точка прямой АВ.

Доказательство:

1) Пусть М - произвольная точка прямой AB, отличная от точек A и В, а 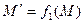, 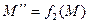. Докажем, что .

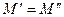2) Так как 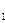f и f 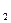- аффинные преобразования, то сохраняются простые отношения точек, т.е.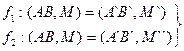

3) Значит, 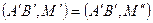или точка 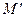совпадает с точкой .

 

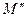Теорема 17.3. Пусть даны два репера 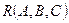и R`(A`,B`,C`). Тогда существует единственное аффинное преобразование, переводящее R в R ` такое, что любая точка М (x, у) репера R переходит в точку M`(x, y) репера R`.

Доказательство:

1.Покажем, что существует аффинное преобразование f, переводящее R в R `:

o Построим отображение f таким образом, что произвольной точке М 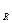(x, y) поставим в соответствие точку М` 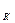(x, y). Такое отображение взаимно однозначно, а значит, оно является преобразованием.

o Покажем, что f – аффинное преобразование.

Пусть М , М , М принадлежат реперу R, причем: , ,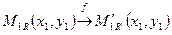

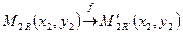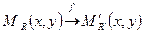
Имеем, что простые отношения точек в различных реперах равны, значит f – аффинное преобразование.

2.Докажем единственность.

o Пусть существует аффинное преобразование f 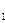, переводящее R в R`.

Пусть М – произвольная точка плоскости. Через точку М проведем прямую так, чтобы она пересекала какие-нибудь две из прямых AB, ВС, АС в различных точках N и P. По лемме 17.2 получаем f(N) = f 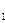(N), f(P) = f 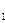(P). Отсюда, используя лемму 17.2, имеем: f(M) = f 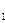(M).

o Таким образом, отображения f и f 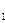совпадают, т.е. f – единственное аффинное преобразование.

 

Следствие 17.4. Если точки А, B, C не лежат на одной прямой и являются неподвижными точками аффинного преобразования, то такие точки тождественны.

Свойства аффинного преобразования:

o Аналогичны свойствам движения (без флага).

o Любое аффинное преобразование либо сохраняет, либо меняет ориентацию плоскости.

Аналитические выражения аффинного преобразования

Исходя из формул преобразования аффинной системы координат, имеем:

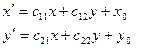
Если определитель системы 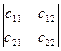> 0, то реперы R и R `, рассматриваемые при аффинном преобразовании, одинаково ориентированы и аффинное преобразование является преобразованием первого рода. В противном случае, реперы противоположно ориентированы и аффинное преобразование есть преобразование второго рода.

Определение 17.5. Нетождественное аффинное преобразование называется перспективно – аффинным (родственным) преобразованием (родством), если оно имеет, по крайней мере, две неподвижные точки.

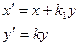- аналитические выражения перспективно-аффинного преобразования

Свойства перспективно-аффинного преобразования:

1. Любая точка прямой, проходящей через две неподвижные точки перспективно-аффинного преобразования, является неподвижной;

2. Прямые, соединяющие соответственные точки родства, не лежащие на его оси, параллельны или совпадают;

3. Если прямая пересекает ось родства в некоторой точке, то ее образ проходит через эту точку;

4. Если прямая параллельна оси родства, то ее образ также параллелен оси.