Лекция №15
Движение. Виды движений. Классификация движений плоскости.
Группа движений плоскости и ее подгруппы.
Определение 15.1. Преобразование плоскости, сохраняющее расстояние, называется движением (перемещением).
Наиболее простейшим примером движения является тождественное преобразование плоскости на себя, при котором каждая её точка переходит в себя.
Определение 15.2. Репером называется упорядоченная тройка точек, не лежащих на одной прямой.
Обозначается: R (A, B, C).
Репер является аффинным, если ΔАВС произвольный.
Репер называется ортонормированным, если ΔАВС – прямоугольный,
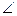 А=90º, AB=АС=1, А – начало репера, В и C – вершины репера.
А=90º, AB=АС=1, А – начало репера, В и C – вершины репера.
Теорема 15.3. При движении репер R, образованный точками A, В, С, переходит в репер R`, образованный точками A`, B`, C`, причем это движение единственно и при этом движении 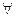 точка М
точка М 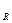 (x,y) переходит в точку М`
(x,y) переходит в точку М` 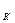 (x,y).
(x,y).
Доказательство:
1. Докажем, что 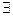 такое движение. Построим отображение плоскости на себя g: γ → γ такое, что R=(A, B, C) →R`=(A`, B`, C`) и М
такое движение. Построим отображение плоскости на себя g: γ → γ такое, что R=(A, B, C) →R`=(A`, B`, C`) и М 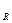 (x,y)→М`
(x,y)→М` 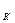 (x,y).
(x,y).
Реперы R и R` ортонормированные, тогда по построенному отображению имеем, что точка А 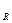 (0,0)→А`
(0,0)→А` 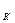 (0,0), В
(0,0), В 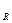 (1,0)→В`
(1,0)→В` 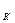 (1,0), С
(1,0), С 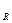 (0,1)→С`
(0,1)→С` 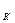 (0,1). Это отображение является взаимно однозначным и значит, оно будет преобразованием плоскости γ на себя.
(0,1). Это отображение является взаимно однозначным и значит, оно будет преобразованием плоскости γ на себя.
2. Докажем, что это преобразование сохраняет расстояние.
Пусть точка М1 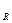 (x1,y1), М2
(x1,y1), М2 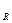 (x2,y2). Тогда М1
(x2,y2). Тогда М1 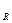 (x1,y1)→М1`
(x1,y1)→М1` 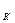 (x1,y1), М2
(x1,y1), М2 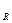 (x2,y2)→М2`
(x2,y2)→М2` 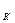 (x2,y2).
(x2,y2).
M1M2 = 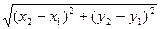
M1`M2`= 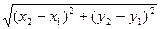
Значит, преобразование плоскости γ в себя является движением.
3. Докажем, что это движение единственное.
Предположим, что  движение g1: γ→ γ.
движение g1: γ→ γ.
При движении g1 точка М  (x,y)→М``
(x,y)→М``  (x,y).
(x,y).
При движении g точка М 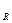 (x,y)→М`
(x,y)→М` 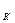 (x,y).
(x,y).
Точка А при движении g1: A 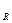
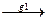 A`
A` 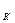 и А
и А 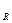
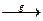 А`
А` 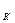
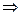 А`M`=A`M`. Значит, точка А` равноудалена от точек M` и M`.
А`M`=A`M`. Значит, точка А` равноудалена от точек M` и M`.
Аналогично показываем равноудаленность точек B` и C` от M` и M``.
Имеем, что точки A`, B`, C` располагаются на одной прямой (серединном перпендикуляре к отрезку M`M`), что противоречит условию теоремы или определению репера.
Следствие 15.4. В любом движении репер переходит в репер, в частности ортонормированный репер переходит в ортонормированный репер.
Свойства движения
1. Движение переводит прямую в прямую, параллельную прямую в параллельную ей прямую.
Доказательство:
o Дано 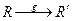 ,
, 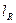 :
: 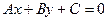 . Каждая точка этой прямой при движении g будет переходить в точку репера R` с теми же координатами. Множество образов этих точек будет принадлежать прямой l`
. Каждая точка этой прямой при движении g будет переходить в точку репера R` с теми же координатами. Множество образов этих точек будет принадлежать прямой l` 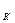 :
: 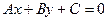
o Пусть 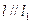 . При движении g:
. При движении g: 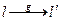 ,
, 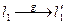 .
.
Предположим, что образы l` и l1` пересекаются в точке M`.
Т.к. движение – это преобразование, а преобразование взаимно однозначно, то прообраз точки M` (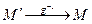 ) должен принадлежать как l так и l1 (M
) должен принадлежать как l так и l1 (M 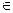 l и M
l и M 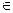 l1)
l1)  l
l  l1, что противоречит условию.
l1, что противоречит условию.
2. Движение переводит полуплоскость с границей A в полуплоскость с границей A`, где A`- образ прямой а;
3. Движение сохраняет простое отношение трех точек прямой;
4. Движение сохраняет отношение «лежать между»;
5. Движение переводит отрезок AB в отрезок A`B`. При этом середина отрезка AB переходит в середину отрезка A`B`;
6. Движение переводит угол в равный ему угол, луч в луч;
7. Движение переводит взаимно перпендикулярные прямые во взаимно перпендикулярные прямые;
8. При движении флаг переводится во флаг (флагомназывается тройка, состоящая из точки, луча и полуплоскости, где О – точка плоскости, h - луч, исходящий из этой точки, α – полуплоскость, граница которой содержит луч h)
Определение 15.5. Два репера, состоящие из R = (O, A, B) и R`= (O`, A`, B`), называются одинаково ориентированными (противоположно ориентированными), если базисы 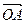 ,
, 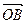 и
и 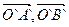 одинаково ориентированы (противоположно ориентированы).
одинаково ориентированы (противоположно ориентированы).
Говорят, что реперы одинаково ориентированы (противоположно ориентированы), если 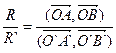 > 0 (<0).
> 0 (<0).
Преобразование точек плоскости сохраняет ориентацию плоскости или меняет ориентацию плоскости, если любой репер и его образ сохраняют ориентацию или меняют ориентацию.
Теорема 15.6. Любое движение либо сохраняет ориентацию, либо меняет ориентацию плоскости.
Аналитические выражения движения
Определение 15.7. Движение, не меняющее ориентацию, называется движением первого рода.
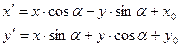
Определение 15.8. Движение, меняющее ориентацию, называется движением второго порядка.
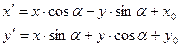
Объединив выражения движений 1-го рода и 2-го рода, можно записать следующие формулы:
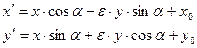
o Если ε = 1, то движение первого рода,
o Если ε = -1, то движение второго рода.
Теорема 15.9. Если в ортонормированном репере даны аналитические выражения вида x` = а 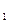 x + b
x + b 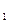 y + x
y + x 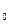 , y` = a
, y` = a 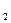 x + b
x + b 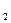 y + y
y + y 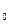 , где матрица, составленная из коэффициентов,
, где матрица, составленная из коэффициентов, 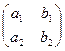 - ортогональная (
- ортогональная (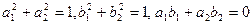 ), то преобразование, рассматриваемое этими выражениями, является движением.
), то преобразование, рассматриваемое этими выражениями, является движением.
Если определитель этой матрицы, составленный из её коэффициентов, равен 1, то преобразование является движением 1-го рода; если определитель равен -1, то это движение 2-го рода.
Классификация движений
В основу классификации движений плоскости положено наличие инвариантных точек и инвариантных прямых.
Определение 15.10. Точка плоскости называется инвариантной (неподвижной), если при преобразовании оно переходит в себя.
Определение 15.11. Прямая называется инвариантной (неподвижной), если при преобразовании любая её точка переходит в точку этой же прямой.
Прямая, любая точка которой при преобразовании переходит в себя, называется прямой инвариантных точек. Прямая инвариантных точек является частным случаем инвариантных прямых.
Лемма 15.12. Если движение g не имеет инвариантных точек, то это движение имеет, хотя бы, одну инвариантную прямую.
Доказательство:
1. Пусть точка A – произвольная точка плоскости. A  A1, A
A1, A 
 A
A 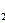 .
.
2. По условию леммы точки A, A 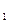 , A
, A 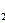 различны (они не совпадают).
различны (они не совпадают).
а) если А, A 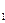 , A
, A 
 а, то очевидно, что а – инвариантная прямая.
а, то очевидно, что а – инвариантная прямая.
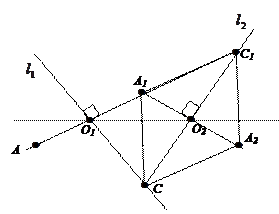 б) если А, A
б) если А, A  , A
, A 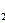
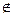 а.
а.
АО  = O
= O  A
A 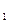 , А
, А 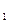 О
О 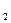 = O
= O 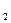 A
A 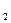 .
.
Докажем, что прямая O 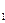 О
О 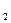 является инвариантной.
является инвариантной.
o Построим серединный перпендикуляр l 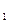 к отрезку АA
к отрезку АA 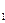 и серединный перпендикуляр l
и серединный перпендикуляр l 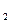 к отрезку A
к отрезку A 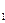 A
A 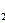 .
. 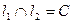 . Очевидно,
. Очевидно, 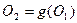 , поэтому
, поэтому 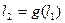 .
.
Так как 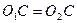 , то точка
, то точка 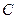 прямой
прямой 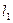 переходит либо в ту же точку
переходит либо в ту же точку 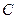 прямой
прямой 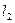 , либо в точку
, либо в точку 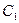 , симметричную точке
, симметричную точке 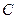 относительно точки
относительно точки 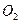 .
.
Первый случай не может иметь места, так как 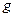 не имеет неподвижных точек, поэтому
не имеет неподвижных точек, поэтому 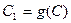 . Таким образом, прямая
. Таким образом, прямая 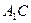 переходит в параллельную ей прямую
переходит в параллельную ей прямую 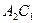 и четырехугольник
и четырехугольник 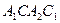 - параллелограмм.
- параллелограмм.
o Найдем образ прямой O  O
O  при этом движении.
при этом движении.
Пусть прямая m является образом прямой O  O
O  .
.
Так как О 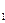 O
O 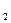
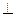 A
A 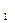 C, то образ прямой m перпендикулярен образу прямой A
C, то образ прямой m перпендикулярен образу прямой A 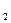 C
C 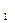 . Но A
. Но A 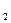 C
C 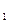
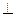 O
O 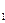 O
O 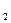 , то есть m совпадает с
, то есть m совпадает с 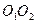 . Значит, значит
. Значит, значит 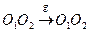 , т.е. O
, т.е. O 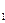 O
O 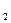 является инвариантной.
является инвариантной.
Лемма 15.13. Если движение g переводит луч h в себя, то это движение либо тождественное преобразование, либо отражение от некоторой прямой, содержащей луч h.
Движение 1-го рода.
1. Движение g имеет две неподвижные точки A и В. В этом случае g является либо тождественным преобразованием по лемме, либо отражением.
2. Движение g содержит одну неподвижную точку. Движение является поворотом на угол α.
o 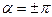 – центральная симметрия, в ней бесконечно много инвариантных прямых, проходящих через центр симметрии;
– центральная симметрия, в ней бесконечно много инвариантных прямых, проходящих через центр симметрии;
o 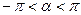 – инвариантных прямых нет.
– инвариантных прямых нет.
3. Движение g не имеет ни одной инвариантной точки. Движение является параллельным переносом на вектор 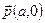 . Любая прямая, параллельная
. Любая прямая, параллельная 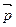 является инвариантной.
является инвариантной.
Движение 2-го рода.
1. Движение g имеет прямую инвариантных точек. Движение является осевой симметрией.
2. Движение не имеет инвариантных точек. В этом случае движение представляет собой произведение осевой симметрии на параллельный перенос g = s∙f, где s – осевая симметрия, f – параллельный перенос и называется скользящей симметрией.






