Пусть А и В — два произвольных множества. Если существуют взаимно однозначное
отображение f множества А на подмножество В1множества В и взаимно однозначное отображение g множества В на подмножество А1 множества А, то А и В эквивалентны.
Доказательство см Колмогоров Фомин, стр. 33
Если эквивалентны два конечных множества, то они состоят из одного и того же числа элементов. Если же эквивалентные между собой множества М и N произвольны, то говорят, что М и N имеют одинаковую мощность.
Определение 10.5(3)
Таким образом, мощность — это то общее, что есть у любых двух эквивалентных между собой множеств. Для конечных множеств понятие мощности совпадает с привычным понятием числа элементов множества. Мощность множества натуральных чисел (т. е. любого счетного множества) обозначается символом ﬡ0 (читается: «алеф нуль»). Про множества, эквивалентные множеству всех действительных чисел отрезка [0,1], говорят, что они имеют мощность континуума. Эта мощность обозначается символом с (или символом ﬡ).
Для мощностей конечных множеств, т. е. для натуральных чисел, кроме понятия равенства имеются также понятия «больше» и «меньше». Попытаемся распространить эти последние на бесконечные мощности.
Пусть А и В — два произвольных множества, а m(А) и m(В) — их мощности. Тогда логически возможны следующие случаи:
1. А эквивалентно некоторой части множества В, и В эквивалентно некоторой части множества А.
2. А содержит некоторую часть, эквивалентную В, но в В нет части, эквивалентной А.
3. В содержит некоторую часть, эквивалентную А, но в А нет части, эквивалентной В.
4. Ни в одном из этих двух множеств нет части, эквивалентной другому.
В первом случае множества А и В в силу теоремы Кантора- Бернштейна эквивалентны между собой, т.е. m(А) = m(В). Во втором случае естественно считать, что m(А) > m(В), а в третьем, — что m(А) < m(В). Наконец, в четвертом случае нам пришлось бы
считать, что мощности множеств А и В несравнимы между собой.
Но на самом деле этот случай невозможен. См Колмогоров, Фомин
Итак, любые два множества А и В либо эквивалентны между собой (и тогда m(А) = m(В)), либо удовлетворяют одному из двух соотношений: m(А) < m(В) или m(А) > m(В).
Можно сказать, что счетные множества — это «самые маленькие» из бесконечных множеств, а затем показали, что существуют и бесконечные множества, бесконечность которых имеет более «высокий порядок», — это множества мощности континуума.
А существуют ли бесконечные мощности, превосходящие мощность континуума? Вообще, существует ли какая-то «наивысшая» мощность или нет? Оказывается, верна следующая теорема.
Теорема 10.5.
Пусть М — некоторое множество и пусть 
— множество, элементами которого являются всевозможные подмножества множества М. Тогда 
имеет мощность большую, чем мощность исходного множества М.
Легко видеть, что мощность m множества
Ш не может быть меньше мощности т исходного множества М, действительно, «одноэлементные» подмножества из М образуют в 
часть, эквивалентную множеству М. Остается доказать, что мощности m и т не совпадают. Пусть между элементами а, b,... множества М и какими-то элементами А, В,... множества 
(т.е. какими-то подмножествами из М) установлено взаимно однозначное соответствие
Покажем, что оно наверняка не исчерпывает всего . Сконструируем такое множество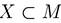 
, которому не соответствует никакой элемент из М. Пусть X — совокупность элементов из М, не входящих в те подмножества, которые им соответствуют. Подробнее: если 
то элемент а мы не включаем в X, а если 
то мы включаем элемент а в X. Ясно, что X есть подмножество множества М, т.е. некоторый элемент из . Покажем, что подмножеству X не может соответствовать никакой
элемент из М. Допустим, что такой элемент 
существует; посмотрим, будет ли он содержаться в X или нет? Пусть 
но ведь по определению в X входит всякий элемент, не содержащийся в подмножестве, которое ему соответствует, следовательно,
элемент х должен быть включен в X. Обратно, предположив, что х содержится в X, мы получим, что х не может содержаться в X, так как в X включены только те элементы, которые не входят в соответствующие им подмножества. Итак, элемент ж, отвечающий
подмножеству X, должен одновременно и содержаться, и не содержаться в X. Отсюда следует, что такого элемента вообще не существует, т. е. что взаимно однозначного соответствия между элементами множества М и всеми его подмножествами установить нельзя. Теорема доказана.
Итак, для любой мощности мы действительно можем построить множество большей мощности, затем еще большей и т.д., получая, таким образом, не ограниченную сверху шкалу мощностей.
Замечание 10.5
Мощность множества 
обозначают символом 2m, где m — мощность М. (Такое число подмножеств нетрудно получить, рассмотрев случай подмножеств конечного множества) Таким образом, предыдущую теорему можно выразить неравенством m < 2m. В частности, при m= ﬡ0 получаем неравенство ﬡ0 < 
.
Можно показать, что 
, т. е. мощность множества всех подмножеств натурального ряда равна мощности континуума.
