Лекция № 6 (24.10.16)
6. НАПРЯЖЁННОЕ СОСТОЯНИЕ МАССИВА В ОКРЕСТНОСТИ НЕЗАКРЕПЛЁННОЙ ВЫРАБОТКИ
6.1. Расчётная схема
Проходка выработки осуществляется в массиве, находящемся под действием гравитационных сил, т.е., в среде с установившимся начальным полем напряжений.
Применение упругой модели и принципа независимости действия сил позволяет учесть первоначальное напряжённое состояние, путём рассмотрения напряжения в массиве, ослабленного выработкой, как сумму начальных напряжений и дополнительных (снимаемых) напряжений.
Понятие снимаемых напряжений ввёл профессор Родин для моделирования образования выработки в напряжённом массиве.
Рис. 6.1 Схема для определения полных напряжений в весомом массиве как суммы начальных и дополнительных (снимаемых) напряжений
Начальному полю напряжений в массиве соответствует начальное поле перемещений и деформаций, которые произошли до начала проведения выработки. Следовательно, деформации и перемещения, происходящие в массиве вследствие образования выработки, вызываются только снимаемыми напряжениями.
Для определения напряжений в массиве, ослабленного выработкой круглого сечения используется решение плоской задачи упругости для полубесконечного весомого массива, ограниченного земной поверхностью L и ослабленного выработкой с контуром L1.
Рис. 6.2.Схема для определения напряжений в массиве, моделируемым упругой средой, ослабленным выработкой круглого сечения
Искомые компоненты напряжений могут быть представлены в виде суммы
(6.1)
где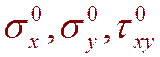 
- начальные напряжения, действовавшие в массиве до образования выработки,
где 
- дополнительные снимаемые напряжения, вызванные образованием выработки,
Компоненты полных и начальных напряжений удовлетворяют системе дифференциальных уравнений равновесия:
(6.2)
и условию совместности деформаций:
(6.3)
Компоненты дополнительных напряжений удовлетворяют, в отличие от полных напряжений однородной системе дифференциальных уравнений равновесия при том же уравнении совместности.
Граничные условия для полных напряжений
На поверхности L граничные условия определяются формулами:
sx = 0 и txy=0 (6.4)
На контуре выработки L1 имеют вид
sx cos(n,x)+ txycos(n,y)=0 (6.5)
txycos(n,x)+ sy cos(n,y) =0
Первые условия означают отсутствие касательных и нормальных напряжений на поверхности, вторые отсутствие напряжений на контуре выработки.
(n,x) и (n,y) углы между нормалью к контуру кругового выреза и осями х,у.
Граничные условия для начальных напряжений на поверхности L:
sx = 0 и txy=0 (6.6)
В качестве частного решения неоднородной системы уравнений (6.2) можно взять поле начальных напряжений:
(6.7)
