Лабораторная работа №5
Определение коэффициентов сил
Трения качения
Тверь
Цель работы: Определение коэффициентов сил
Трения качения
Приборы и принадлежности: Установка Лебедева для определение коэффициентов сил трения качения,набор материалов
Введение.
Трение качения обусловлено взаимной деформацией тел, которая нессиметрична относительно катящегося тела (цилиндр, колесо). Реакция опоры (почва, рельсы) поэтому несколько смещена (см. рис. 1) вперед по направлению движения цилиндра и не проходит через его ось. Это приводит к появлению момента реакции опоры относительно оси вращения, момента силы трения качения:
(1)
где k—плечо силы коэффициент трения качения, имеющий раз-мерность длины,
N—нормальная составляющая реакция опоры равная весу P цилиндра.
В технике пользуются обычно величиной силы, необходимой для перекатывания колеса и приложенной к его оси:
, (1а)
где R – радиус колеса, Р – его вес.
В ряде случаев наличие силы сопротивления перекатыванию объясняют неполной упругостью материала тел, упругим гистерезисом. Теоретическое рассмотрение процесса перекатывания с учетом величин, характеризующих материал тел, скорости их движения, давления на них, приводит к сложным выражениям для величины этой силы.
Зависимость от радиуса колеса и нагрузки на него в этом случае получается более сложной, что объясняют относительным скольжением деформированных поверхностей тел, к чему и сводят, в
основном, силу сопротивления перекатыванию.
В отдельных случаях наличие этой силы объясняют молекулярным сцеплением.
Уравнения (1) и (1а) следует рассматривать как первые приближения, удобные по причине их простоты, для определения искомой величины в каждом конкретном случае. Полной теории, учи-
тывающей все процессы, сопровождающие перекатывание тел, в нас-
тоящее время не существует.
Описание установки
В работе пользуются методом, предложенным С.Ф.Лебедевым.
Применяется (см. рис. 2) стальной 
цилиндр А, находящийся на метал-лической плите В. Цилиндр закреплен в обойме С, которая имеет стержни D и Е. Первый является стрелкой к шкале H. На втором, проходящем через отверстие в плите, закреплен груз G. Подвижная часть установки может быть названа “маятником”. При отклонении ее от положения равновесия она совершает нелинейные затухающие колебания. Ось цилиндра при этом двигается поступательно, сам цилиндр вращается вокруг этой оси.
Отклонение стрелки на шкале будет (см. рис. 3) следовательно, суммой двух отклонений:
(2)
, (3)
где: a- угол поворота цилиндра, R—его радиус,
L – расстояние от оси цилиндра до шкалы, a - отклонение, связанное с вращением цилиндра вокруг его оси.
a1-отклонение оси цилиндра. Для суммарного отклонения получим:
(4)
При R много меньшем L можно пренебречь величиной 
и считать за отклонение по шкале величину:
(5)
Если a<5°,то для начального отклонения a 
,a и отклонения после n полных периодов соответственно, получим
(6)
Уменьшение угла отклонения за известное число периодов колебаний маятника дает возможность (см. ниже) вычислить величину коэффициента трения качения.
Теория метода
Введем формулу для расчета на описанной установке коэффициента трения качения. Считая его независящим от скорости движения маятника, воспользуемся законом сохранения энергии.При начальном отклонении маятника на угол a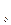 
его потенциальная энергия может быть представлена (см. рис. 4) в виде: 
, (7)
где h0—перемещение по вертикали центра тяжести маятника,
P—его вес,
i--расстояние между точкой центра тяжести и осью маятника через один полный период колебания маятника аналогично получим:
(8)
где a1—угол отклонения маятника через один полный период колебаний.
Уменьшение потенциальной энергии будет:
(9)
При a <50 sin(a/2) ≈ a/2 получим:
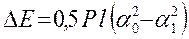(10)
Это уменьшение энергии, если пренебречь силами трения о воздух вызвано работой против сил трения качения. За один полный период колебания маятника работа может быть (см. рис.5) записана так:
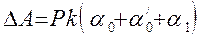(11)
где k—коэффициент трения качения,
a0/-- угол отклонения после одного полупериода.
Исключим из этого уравнения угол a0/. Пусть Da-- уменьшение угла отклонения за один полупериод. Тогда можем записать:
(12)
Из уравнений (11) и (12) получим:
(13)
Приравнивая уравнения (10) и (13), получим:
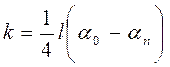(14)
Для n полных периодов колебаний имеем:
(15)
Пользуясь уравнением (6), окончательно получим:
(16)
Этой формулой и пользуются для вычисления величины коэффициента трения качения.
Измерения.
Для измерения коэффициента трения качения для пары сталь—материал пластины определяют n - число периодов колебаний маятника.
1. Под цилиндр маятника на плите кладутся пара образцов из одного материала указанные преподавателем или лаборантом (сталь-образец). Цилиндр на плите должен занимать положение, не препятствующее его перекатыванию.
2. Совместить ноль шкалы с концом стрелки покоящегося маятника.
3 Отклонения маятника производится вручную, очень осторожно:
перекатывание цилиндра при отклонении маятника не должно сопровождаться его проскальзыванием по плите.
4. Начальное отклонение маятника по шкале a0 взято 2,5см
5. Его конечное отклонение an после n полных периодов колебаний 1,0см.
6. В этом интервале отклонений маятника при a0- an =1,5см. (т.е. по шкале от метки 2,5см и до метки 1 см.)и отсчитывается число n его полных периодов колебаний.
Отсчет производится 5 раз.
Данные занести в таблицу.
| n | Образец №1 | Образец №2 | Образец №3 |
После определения коэффициента трения качения для пары сталь—материал пластины, их определяют и для других пар материалов указанных преподавателем или лаборантом.
Величины l, L даются на установке.
Пользуясь средним арифметическим значением n по формуле (16) вычисляют коэффициент трения качения для каждого из образцов.
Поверхность пластинок обрабатывалась на обычном станке и не шлифовалась. Профиль шероховатости, поэтому, не одинаков в различных направлениях. Естественно, что при перекатывании цилиндра вдоль по длине пластинки и поперек ее будут получаться несколько различные значения величины коэффициента трения качения. Не следует, поэтому изменять положение пластинок при повторных измерениях. Полученные значения коэффицентов трения качения для разных пар сравнивают между собой.
Данные занести в таблицу
| образцы | n | Δ n | (а0-аn) мм | Δ (а0-аn) мм | l, мм | L, мм | k, мм | ε % | Δ k, мм | |
Расчитать относительную погрешность по формуле:
,
(а0-аn) = 1 мм, n = 1
Найти абсолютную погрешность и записать ответ
КОНТРОЛЬНЫЕ ВОПРОСЫ
1) Каковы причины возникновения трения качения?
2) Почему колебания, которые подвижная часть установки, являются нелинейными?
3) Момент силы относительно оси. Работа при вращательном движении.
4) Обосновать формулу F=kP/R. К какой линии приложена сила F.
5) Как называется коэффициент k? Каковы его физический смысл и размерность?
6) Обосновать формулу (11).
7) Вывести расчетную формулу (16).
8) Сравните значения коэффициентов трения k, полученные для различных пар материалов и объясните результаты.
9) Оцените силу трения качения F=kP/R для любой пары материалов и сравните ее с силой тренния скольжения, найденной из закона Кулона—Амонтона Fc=mP. Коэффициент m возьмите из таблицы или результатов работы №7. Сравните F и Fc.
ЛИТЕРАТУРА.
1.С.П.Стрелков.Механика. Изд. ”Наука”. 1975,Гл.8,§§72—75.
2.А.Н.Матвеев. Механика и теория относительности. “Высшая школа”,1976, Гл 12,§56.
