I. Последовательности
1. Элементы теории функций и функционального анализа. Функциональная зависимость. Пространство. Предел числовой последовательности и его свойства. Бесконечно малые и бесконечно большие величины. Предел функции в точке и на бесконечности. Эпсилон-окрестность точки.
2. Основные теоремы о пределах. I и II замечательные пределы:
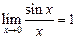 и
и  .
.
Число е. Натуральные логарифмы. Определения и исследования некоторых основных элементарных функций (а х, log a x, хb, sh x, ch x, th x, cth x). Их графики.
3. Сравнение бесконечно малых. Эквивалентность некоторых элементарных функций. Замена функций под знаком предела на эквивалентную ей. Непрерывность функции в точке и на множестве. Точки разрыва функции.
II. Дифференциальное исчисление
4. Производная функции, ее геометрический и механический смысл. Операции дифференцирования. Таблицы производных элементарных функций. Уравнение касательной и нормали.
5. Производные тригонометрических функций, обратно тригонометрических функций. Производные логарифмической и показательной функции. Производные сложных функций. Логарифмическое дифференцирование. Дифференцирование неявных, параметрически заданных функций.
6. Дифференциал, его геометрический смысл. Применение дифференциала в приближенных вычислениях. Применение дифференциалов в приближенных вычислениях. Основные теоремы дифференциального исчисления.
7. Некоторые применения теорем о среднем значении. Правило Лопиталя для вычисления пределов функций. Исследование функций с помощью производных. Условия возрастания и убывания на промежутке. Необходимое и достаточное условия существования локального экстремума функция.
8. Исследование функции на выпуклость, точки перегиба. Асимптоты кривых. Общая схема построения эскизов графиков с использованием дифференциального исчисления. Наибольшее и наименьшее значения функции на отрезке.
III. Теория функций комплексного переменного
9. Функции нескольких переменных. Область определения, графики функций. Функциональные пространства. Метрические пространства. Пространство Rn. Расстояние. Предел функции, непрерывность. Частные производные I порядка, полный дифференциал. Производная неявной функции. Частные производные высших порядков. Касательная, плоскость и нормаль к поверхности. Экстремумы функции нескольких переменных. Производная по направлению. Градиент.
10. Комплексные числа, действия с ними. Изображение комплексных чисел на плоскости. Модуль и аргумент комплексного числа. Алгебраическая, тригонометрическая, показательная формы записи комплексных чисел. Формулы Эйлера, Муавра.






